2008 Alternate AIME Math Jam
Go back to the Math Jam ArchiveAoPS instructors will lead a discussion on all 15 problems from the 2008 Alternate AIME.
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.
Facilitator: Dave Patrick
DPatrick18:58:52
Hello and welcome to the 2008 AIME II Math Jam!
Hello and welcome to the 2008 AIME II Math Jam!
DPatrick18:59:00
Before we get started, please note that this classroom is moderated, meaning that students can type into the classroom, but only the moderator can choose a comment to drop into the classroom. This helps keep the discussion organized and on track.
Before we get started, please note that this classroom is moderated, meaning that students can type into the classroom, but only the moderator can choose a comment to drop into the classroom. This helps keep the discussion organized and on track.
DPatrick18:59:11
This also means that only well-written comments will be dropped into the classroom, so please take time to write responses that are complete and easy to read.
This also means that only well-written comments will be dropped into the classroom, so please take time to write responses that are complete and easy to read.
DPatrick18:59:28
Due to the size of this Math Jam, I probably won't be able to respond to individual questions, nor post a lot of responses. Please do not complain if your comments are not responded to.
Due to the size of this Math Jam, I probably won't be able to respond to individual questions, nor post a lot of responses. Please do not complain if your comments are not responded to.
DPatrick18:59:44
I don't claim that the solutions that we'll present today are the "definitive" or "best" solutions to each problem. Many of the problems have more than one good approach. We don't have time to consider every possible approach to every problem.
I don't claim that the solutions that we'll present today are the "definitive" or "best" solutions to each problem. Many of the problems have more than one good approach. We don't have time to consider every possible approach to every problem.
DPatrick19:00:05
Also, these solutions are not necessarily the fastest or slickest, but these solutions are the one that (to me) are the most logical or natural, or the one that you'd be most likely to think of on your own.
Also, these solutions are not necessarily the fastest or slickest, but these solutions are the one that (to me) are the most logical or natural, or the one that you'd be most likely to think of on your own.
DPatrick19:00:16
And with that, let's get started!
And with that, let's get started!
DPatrick19:00:22
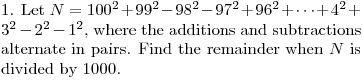
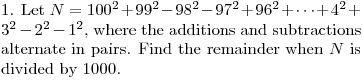
DPatrick19:00:25
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-214549086.gif
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-214549086.gif
DPatrick19:00:28
(I will post a link to each problem after I post the problem statement. You should be able to click on the link to view the problem in a separate window. You may have to hold the Ctrl key, and depending on how your popup-blocker is configured it may not work at all for you.)
(I will post a link to each problem after I post the problem statement. You should be able to click on the link to view the problem in a separate window. You may have to hold the Ctrl key, and depending on how your popup-blocker is configured it may not work at all for you.)
charles.du19:01:09
pair up every other number
pair up every other number
charles.du19:01:09
and use difference of squares
and use difference of squares
frodo19:01:09
Sums and differences of squares
Sums and differences of squares
karatemagic719:01:11
pair 100^2 with 98^2 and 99^2 with 97^2 and 96^2 with 94^2 ...
pair 100^2 with 98^2 and 99^2 with 97^2 and 96^2 with 94^2 ...
DPatrick19:01:30
What we notice is that the numbers come in pairs.
What we notice is that the numbers come in pairs.
DPatrick19:01:55
One way to pair them is (100^2 - 98^2) + (99^2 - 97^2) and so on.
One way to pair them is (100^2 - 98^2) + (99^2 - 97^2) and so on.
frodo19:02:22
198*2+196*2+190*2+188*2+184*2+182*2+...
198*2+196*2+190*2+188*2+184*2+182*2+...
DPatrick19:02:53
Right...the slight downside of this is when you sum them, there are gaps.
Right...the slight downside of this is when you sum them, there are gaps.
frodo19:03:04
the last two should be 182*2+180*2+...
the last two should be 182*2+180*2+...
DPatrick19:03:14
Right...
Right...
Bicameral19:03:19
Every quadruple, such as 4^2+3^2 -2^2-1^2=20, and differ by 32, so on........ Then, you can use the Arithmetic Series Sum formula..
Every quadruple, such as 4^2+3^2 -2^2-1^2=20, and differ by 32, so on........ Then, you can use the Arithmetic Series Sum formula..
Bicameral19:03:19
8^2+7^2-6^2-5^2 = 52, etc.
8^2+7^2-6^2-5^2 = 52, etc.
DPatrick19:03:28
You could do that too.
You could do that too.
DPatrick19:03:32
There are lots of ways to pair them up.
There are lots of ways to pair them up.
DPatrick19:03:41
Here's what I did, which avoids having to sum a series.
Here's what I did, which avoids having to sum a series.
DPatrick19:03:48
First note that we can ignore the 100^2 term at the beginning, since it doesn't leave a remainder when divided by 1000.
First note that we can ignore the 100^2 term at the beginning, since it doesn't leave a remainder when divided by 1000.
DPatrick19:04:05
After that, the terms come in pairs: (99^2 - 98^2) - (97^2 - 96^2) + (95^2 - 94^2) - ... + (3^2 - 2^2) - 1.
After that, the terms come in pairs: (99^2 - 98^2) - (97^2 - 96^2) + (95^2 - 94^2) - ... + (3^2 - 2^2) - 1.
DPatrick19:04:27
Each term in parenthesis is just the sum of the two numbers being squared.
Each term in parenthesis is just the sum of the two numbers being squared.
DPatrick19:04:37
For example:
(99^2 - 98^2) = (99+98)(99-98) = 99+98.
For example:
(99^2 - 98^2) = (99+98)(99-98) = 99+98.
frodo19:04:44
It's just 99+98-97-96+95+94-...
It's just 99+98-97-96+95+94-...
kops72319:04:51
all the pairs of pairs have a difference of 4
all the pairs of pairs have a difference of 4
DPatrick19:04:58
Exactly. Our sum is just:
(99+98)-(97+96)+(95+94)-(93+92)+...+(3+2)-1.
Exactly. Our sum is just:
(99+98)-(97+96)+(95+94)-(93+92)+...+(3+2)-1.
DPatrick19:05:17
And the difference between each pair of parenthesis (such as (99+98)-(97+96)) is just 4.
And the difference between each pair of parenthesis (such as (99+98)-(97+96)) is just 4.
3468Yz19:05:25
There are 24 quadruples.
There are 24 quadruples.
DPatrick19:05:38
Right. We have 24 sets of four numbers each summing to 4, and then an extra +4 at the end. (Or we can add 0^2 to the end and then we just have 25 sets.)
Right. We have 24 sets of four numbers each summing to 4, and then an extra +4 at the end. (Or we can add 0^2 to the end and then we just have 25 sets.)
DPatrick19:05:44
Thus the sum is 25*4 = 100.
Thus the sum is 25*4 = 100.
DPatrick19:06:32
As I said, there were lots of ways to do it...I don't necessarily think any one method is better.
As I said, there were lots of ways to do it...I don't necessarily think any one method is better.
DPatrick19:06:40


DPatrick19:06:45
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-133046975.gif
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-133046975.gif
DPatrick19:07:01
One key part of this problem is reading it carefuly.
One key part of this problem is reading it carefuly.
DPatrick19:07:09
...or better yet, carefully with 2 l's.
...or better yet, carefully with 2 l's.
dingzhou19:07:30
assign variables and set up equations
assign variables and set up equations
3468Yz19:07:30
Consider the time the two people spend biking and on breaks.
Consider the time the two people spend biking and on breaks.
DPatrick19:07:54
Right. The key quantity in this problem is time. So I'd write equations in terms of time, not rate or distance.
Right. The key quantity in this problem is time. So I'd write equations in terms of time, not rate or distance.
DPatrick19:08:08
Also, a key word in the problem statement is the word "arrive".
Also, a key word in the problem statement is the word "arrive".
samk19:08:30
he stops 49 times
he stops 49 times
samk19:08:30
and she 24
and she 24
frodo19:08:30
They don't take a break at the end of their ride.
They don't take a break at the end of their ride.
DPatrick19:08:41
Exactly. We have to be sure not to count the break at Mile 50.
Exactly. We have to be sure not to count the break at Mile 50.
DPatrick19:08:58
Suppose it takes Rudolph m minutes to bike one mile. How long does it take Jennifer?
Suppose it takes Rudolph m minutes to bike one mile. How long does it take Jennifer?
miller4math19:09:17
4/3 m
4/3 m
3468Yz19:09:17
4/3 m
4/3 m
ra524919:09:19
4/3m
4/3m
DPatrick19:09:23
It takes her (4/3)m minutes.
It takes her (4/3)m minutes.
DPatrick19:09:34
She rides at 3/4 the rate, so it takes here 4/3 the time.
She rides at 3/4 the rate, so it takes here 4/3 the time.
DPatrick19:09:44
Now our equation is clear.
Now our equation is clear.
DPatrick19:09:50
Rudolph needs 50m minutes for the biking, plus 49 rest stops of 5 minutes each, for a total of 50m + 245 minutes.
Rudolph needs 50m minutes for the biking, plus 49 rest stops of 5 minutes each, for a total of 50m + 245 minutes.
DPatrick19:10:03
Jennifer needs (200/3)m minutes for the biking, plus 24 rest stops of 5 minutes each, for a total of (200/3)m + 120 minutes.
Jennifer needs (200/3)m minutes for the biking, plus 24 rest stops of 5 minutes each, for a total of (200/3)m + 120 minutes.
DPatrick19:10:16
So 50m + 245 = (200/3)m + 120.
So 50m + 245 = (200/3)m + 120.
DPatrick19:10:30
I made life easy on myself by only thinking about the time and not the rates.
I made life easy on myself by only thinking about the time and not the rates.
DPatrick19:10:47
Now we just have to solve.
Now we just have to solve.
3468Yz19:11:15
50/3 m = 125
50/3 m = 125
charles.du19:11:15
125=50/3m
125=50/3m
dingzhou19:11:17
m=15/2
m=15/2
DPatrick19:11:24
Solving gives (50/3)m = 125, so 50m = 375 and m = 375/50.
Solving gives (50/3)m = 125, so 50m = 375 and m = 375/50.
DPatrick19:11:47
Then we can use either equation to compute the number of minutes necessary.
Then we can use either equation to compute the number of minutes necessary.
charles.du19:11:51
plug in
plug in
DPatrick19:11:55
Thus the total time is 50(375/50) + 245 = 375 + 245 = 620 minutes.
Thus the total time is 50(375/50) + 245 = 375 + 245 = 620 minutes.
DPatrick19:12:27


DPatrick19:12:31
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-71537967.gif
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-71537967.gif
ra524919:13:07
after each cut one of the side lengths is reduced by one for a total of 10 centimeters removed from the side lengths
after each cut one of the side lengths is reduced by one for a total of 10 centimeters removed from the side lengths
3468Yz19:13:07
Removing a slice means decreasing one dimension by 1.
Removing a slice means decreasing one dimension by 1.
infinity4ever19:13:13
look at this in terms of the sum of the sidelengths, before and after the cuts
look at this in terms of the sum of the sidelengths, before and after the cuts
dingzhou19:13:13
you notice that everytime you make a cut, 1 cm is taken off of a edge, and theres 10 cuts, so theres a total of 10 cm thats taken off.
you notice that everytime you make a cut, 1 cm is taken off of a edge, and theres 10 cuts, so theres a total of 10 cm thats taken off.
DPatrick19:13:16
Right.
Right.
DPatrick19:13:29
In particular, if we cut a slices in the 10 cm dimension, b slices in the 13 cm dimension, and c slices in the 14 cm dimension, then the volume remaining is (10-a)(13-b)(14-c).
In particular, if we cut a slices in the 10 cm dimension, b slices in the 13 cm dimension, and c slices in the 14 cm dimension, then the volume remaining is (10-a)(13-b)(14-c).
DPatrick19:13:36
And we also have a+b+c = 10.
And we also have a+b+c = 10.
DPatrick19:13:41
(because there are 10 cuts total)
(because there are 10 cuts total)
infinity4ever19:13:48
notice that the largest possible volume left must be a cube
notice that the largest possible volume left must be a cube
DPatrick19:13:49
Why?
Why?
miller4math19:14:06
AM-GM
AM-GM
ra524919:14:06
am-gm
am-gm
dingzhou19:14:13
AM-GM?
AM-GM?
DPatrick19:14:29
Right..to prove what the largest volume can be, we can use the AM-GM inequality.
Right..to prove what the largest volume can be, we can use the AM-GM inequality.
DPatrick19:14:37
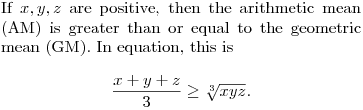
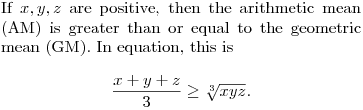
DPatrick19:15:07
So we can plug in 10-a for x, 13-b for y, and 14-c for z.
So we can plug in 10-a for x, 13-b for y, and 14-c for z.
DPatrick19:15:13
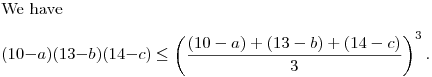
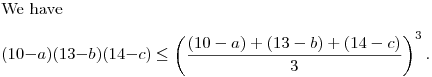
frodo19:15:31
(10+13+14-10)/3=9
(10+13+14-10)/3=9
ra524919:15:35
so after ten cuts the remaining sum length is (10+13+14)-10 = 27, so the largest volume by am-gm is (27/3)^3
so after ten cuts the remaining sum length is (10+13+14)-10 = 27, so the largest volume by am-gm is (27/3)^3
DPatrick19:15:49
Right. We also have a+b+c = 10, so the numerator on the right side is 10+13+14-10 = 27. Thus the right side is just (27/3)^3 = 9^3 = 729.
Right. We also have a+b+c = 10, so the numerator on the right side is 10+13+14-10 = 27. Thus the right side is just (27/3)^3 = 9^3 = 729.
DPatrick19:16:07
This tells us that the volume is at most 729; can we actually achieve the maximum?
This tells us that the volume is at most 729; can we actually achieve the maximum?
dingzhou19:16:21
a=1 b=4 c=5
a=1 b=4 c=5
frodo19:16:21
a=1; b=4; c=5 it works!
a=1; b=4; c=5 it works!
ra524919:16:21
yes, 9by9by9
yes, 9by9by9
DPatrick19:16:27
Equality holds in AM-GM if all the numbers are equal.
Equality holds in AM-GM if all the numbers are equal.
DPatrick19:16:34
So we need 10-a = 13-b = 14-c = 9, and it's easy to see this happens if (a,b,c) = (1,4,5).
So we need 10-a = 13-b = 14-c = 9, and it's easy to see this happens if (a,b,c) = (1,4,5).
DPatrick19:16:41
So the maximum volume is 729.
So the maximum volume is 729.
charles.du19:16:49
can't you just slice off one from the largest dimension every time?
can't you just slice off one from the largest dimension every time?
DPatrick19:17:06
Indeed, if you didn't know AM-GM, you could do an algorithmic procedure called a "greedy algorithm", in which at each step you always cut to remove the smallest possible piece.
Indeed, if you didn't know AM-GM, you could do an algorithmic procedure called a "greedy algorithm", in which at each step you always cut to remove the smallest possible piece.
DPatrick19:17:21
In this problem, it means cutting to reduce the largest dimension by 1.
In this problem, it means cutting to reduce the largest dimension by 1.
DPatrick19:17:29
If you do this, you'll end up at the correct answer of a 9x9x9 block.
If you do this, you'll end up at the correct answer of a 9x9x9 block.
ra524919:17:40
yeah that works too, but you have to make sure it is the largest remaining volume possible by algebra
yeah that works too, but you have to make sure it is the largest remaining volume possible by algebra
DPatrick19:17:48
Right, using algebra (AM-GM) proves that this works.
Right, using algebra (AM-GM) proves that this works.
DPatrick19:17:56
Greedy algorithms don't always work, and it's often hard to prove that they do work when they do. It happens to work for this problem, but to prove it works I think you have to use AM-GM.
Greedy algorithms don't always work, and it's often hard to prove that they do work when they do. It happens to work for this problem, but to prove it works I think you have to use AM-GM.
DPatrick19:18:28
But, on the other hand, the AIME doesn't require proofs! If you're convinced that your answer is correct, it's often a good idea to just go with it.
But, on the other hand, the AIME doesn't require proofs! If you're convinced that your answer is correct, it's often a good idea to just go with it.
DPatrick19:18:39
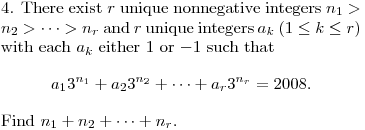
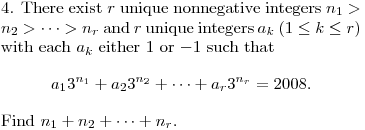
DPatrick19:18:42
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-161817918.gif
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-161817918.gif
infinity4ever19:19:33
guess and check!
guess and check!
DPatrick19:19:41
Since 2008 is (relatively) small, you could just guess and check.
Since 2008 is (relatively) small, you could just guess and check.
stupidityismygam19:19:49
base 3 looks nice
base 3 looks nice
DPatrick19:20:02
A somewhat more systematic way to solve it is to first write 2008 in base 3.
A somewhat more systematic way to solve it is to first write 2008 in base 3.
DPatrick19:20:09
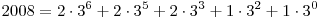
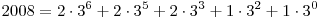
DPatrick19:20:27
Now we have to convert terms of the form 2 * 3^k into terms with coefficients 1 and -1.
Now we have to convert terms of the form 2 * 3^k into terms with coefficients 1 and -1.
ra524919:20:35
express in base 3, if it has a place hold of two then the a_k is -1 for the spot before it, if it has a place hold of 1 then a_k is +1
express in base 3, if it has a place hold of two then the a_k is -1 for the spot before it, if it has a place hold of 1 then a_k is +1
kops72319:20:35
we like the 1's, and a 2 is just the difference of the next power of 3 and the current
we like the 1's, and a 2 is just the difference of the next power of 3 and the current
DPatrick19:20:55
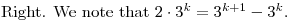
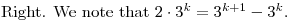
DPatrick19:21:08
So we can replace 2 * 3^6 with 3^7 - 3^6.
So we can replace 2 * 3^6 with 3^7 - 3^6.
DPatrick19:21:30
Now we just systematically replace the terms that have a coefficient of 2.
Now we just systematically replace the terms that have a coefficient of 2.
3468Yz19:21:46
Left to right.
Left to right.
wade19:21:51
deleting the two's
deleting the two's
DPatrick19:21:55
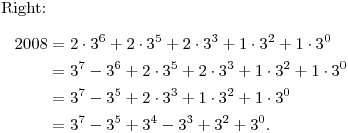
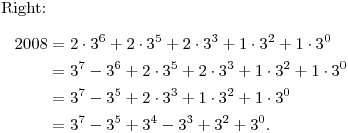
DPatrick19:22:12
As a check, this last sum is 2187 - 243 + 81 - 27 + 9 + 1 which indeed equals 2008.
As a check, this last sum is 2187 - 243 + 81 - 27 + 9 + 1 which indeed equals 2008.
ra524919:22:21
so its 7+5+4+3+2=021
so its 7+5+4+3+2=021
frodo19:22:21
7+5+4+3+2=021
7+5+4+3+2=021
3468Yz19:22:21
7+5+4+3+2=21
7+5+4+3+2=21
DPatrick19:22:28
So the answer is the sum of the exponents, which is 7+5+4+3+2+0 = 021.
So the answer is the sum of the exponents, which is 7+5+4+3+2+0 = 021.
DPatrick19:23:04
I thought this was the least-interesting problem...it didn't have much zazz to it.
I thought this was the least-interesting problem...it didn't have much zazz to it.
DPatrick19:23:16


DPatrick19:23:23
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-166865646.gif
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-166865646.gif
karatemagic719:23:34
draw a picture
draw a picture
charles.du19:23:37
diagram!
diagram!
miller4math19:23:37
pic?
pic?
stupidityismygam19:23:39
best solution: participate in usamts :)
best solution: participate in usamts :)
DPatrick19:23:47
Yeah -- those of you that do a lot of contests might recognize that this problem is nearly identical to USA Math Talent Search Problem 2/2/18 from November 2006.
Yeah -- those of you that do a lot of contests might recognize that this problem is nearly identical to USA Math Talent Search Problem 2/2/18 from November 2006.
DPatrick19:24:04
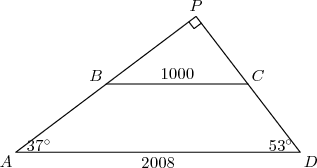
We start by drawing a diagram:
We start by drawing a diagram:
DPatrick19:24:11


DPatrick19:24:13
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/0e0f6b90bfb25201a5a849fe1ee5f472.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/0e0f6b90bfb25201a5a849fe1ee5f472.png
ra524919:24:21
note that 37 and 53 are complimentary
note that 37 and 53 are complimentary
dingzhou19:24:21
37+53=90 yay!
37+53=90 yay!
infinity4ever19:24:21
notice that 37 and 53 are complementary =)
notice that 37 and 53 are complementary =)
DPatrick19:24:37
Right, what is particularly notable is that the two bottom angles sum to 90 degress (that is, they're complementary).
Right, what is particularly notable is that the two bottom angles sum to 90 degress (that is, they're complementary).
asdf419:24:51
extend trapezoid to triangle?
extend trapezoid to triangle?
dingzhou19:24:51
extend AB and DC
extend AB and DC
frodo19:24:51
EXtend AB and CD so they intersect
EXtend AB and CD so they intersect
DPatrick19:25:02
This suggests extending AB and DC so that we have a right triangle.
This suggests extending AB and DC so that we have a right triangle.
DPatrick19:25:07

DPatrick19:25:08
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/c394a1c1544cbee3e8890dc814ee8bdc.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/c394a1c1544cbee3e8890dc814ee8bdc.png
DPatrick19:25:19
Now what?
Now what?
infinity4ever19:25:37
draw the median from P to AD
draw the median from P to AD
dingzhou19:25:37
median to the hypotenuse equals half of it
median to the hypotenuse equals half of it
kops72319:25:37
median to hypoteneus
median to hypoteneus
darkmatter4719:25:37
similar triangles?
similar triangles?
ra524919:25:37
similar...
similar...
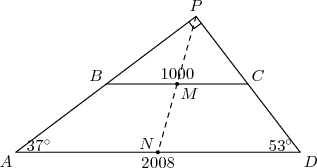
DPatrick19:25:45
We know that PBC and PAD are similar.
We know that PBC and PAD are similar.
DPatrick19:25:53
This means that P, M, and N are all collinear.
This means that P, M, and N are all collinear.
DPatrick19:26:00

DPatrick19:26:01
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/d8af73fb44e75768f4a1716f14928a6f.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/d8af73fb44e75768f4a1716f14928a6f.png
frodo19:26:25
PM=500 PN=1004
PM=500 PN=1004
DPatrick19:26:37
Right: the length of a median to a hypotenuse of a right triangle is half the length of the hypotenuse.
Right: the length of a median to a hypotenuse of a right triangle is half the length of the hypotenuse.
DPatrick19:26:43
(This is because the midpoint of the hypotenuse is the center of the circumcircle of the triangle.)
(This is because the midpoint of the hypotenuse is the center of the circumcircle of the triangle.)
DPatrick19:26:58
So PM = 1000/2 = 500 and PN = 2008/2 = 1004.
So PM = 1000/2 = 500 and PN = 2008/2 = 1004.
asdf419:27:09
1004-500=504
1004-500=504
pascal_162319:27:09
so the answer is 504
so the answer is 504
DPatrick19:27:13
Therefore, MN = PN - PM = 1004 - 500 = 504.
Therefore, MN = PN - PM = 1004 - 500 = 504.
DPatrick19:27:51
There are certainly uglier ways to do this problem...but angles like 37 and 53 are usually not chosen complementary by coincidence!
There are certainly uglier ways to do this problem...but angles like 37 and 53 are usually not chosen complementary by coincidence!
DPatrick19:28:07
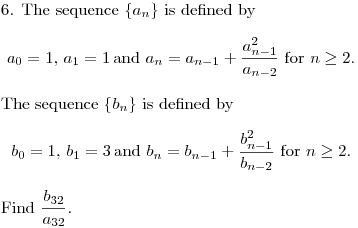
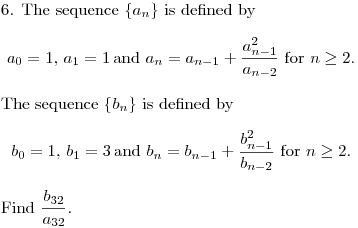
DPatrick19:28:11
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-146988590.gif
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-146988590.gif
ra524919:28:30
list a few terms and find a pattern!
list a few terms and find a pattern!
karatemagic719:28:30
plug in numbers
plug in numbers
dingzhou19:28:30
try to find a pattern
try to find a pattern
charles.du19:28:30
calculate a few terms, and look for a pattern
calculate a few terms, and look for a pattern
DPatrick19:28:36
When it doubt, compute a few terms of the sequences.
When it doubt, compute a few terms of the sequences.
DPatrick19:28:43
I found it slightly helpful in the computation to first factor the recurrence relation:
I found it slightly helpful in the computation to first factor the recurrence relation:
DPatrick19:28:48
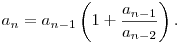
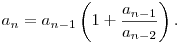
DPatrick19:29:02
(and the same for the b's of course)
(and the same for the b's of course)
DPatrick19:29:14
So we can just start computing a few terms.
So we can just start computing a few terms.
DPatrick19:29:23
a_2 = 1(1+1/1) = 1(2) = 2.
a_2 = 1(1+1/1) = 1(2) = 2.
DPatrick19:29:29
a_3 = 2(1+2/1) = 2(3) = 6.
a_3 = 2(1+2/1) = 2(3) = 6.
DPatrick19:29:35
a_4 = 6(1+6/2) = 6(4) = 24.
a_4 = 6(1+6/2) = 6(4) = 24.
DPatrick19:29:40
a_5 = 24(1+24/6) = 24(5) = 120.
a_5 = 24(1+24/6) = 24(5) = 120.
karatemagic719:29:49
a_n is n!
a_n is n!
delian19:29:49
a_n= n! !!!
a_n= n! !!!
infinity4ever19:29:49
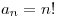
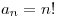
3468Yz19:29:49
a_n=n!
a_n=n!
asdf419:29:49
factorials!
factorials!
DPatrick19:29:59
The pattern looks obvious. a_n = n!.
The pattern looks obvious. a_n = n!.
DPatrick19:30:18
We can prove it (although you don't have to for the AIME). It works for the initial conditions, and:
We can prove it (although you don't have to for the AIME). It works for the initial conditions, and:
DPatrick19:30:23
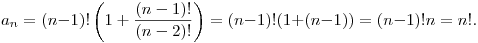
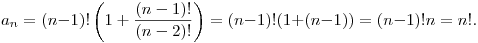
kops72319:30:35
we can prove that fairly easily too... the term outside the parenthesis is (n-1)! and the term inside is n
we can prove that fairly easily too... the term outside the parenthesis is (n-1)! and the term inside is n
DPatrick19:30:38
Exactly.
Exactly.
DPatrick19:30:51
We can do the same thing with the b's:
We can do the same thing with the b's:
DPatrick19:31:01
b_2 = 3(1+3/1) = 3(4) = 12.
b_2 = 3(1+3/1) = 3(4) = 12.
DPatrick19:31:11
b_3 = 12(1+12/3) = 12(5) = 60.
b_3 = 12(1+12/3) = 12(5) = 60.
DPatrick19:31:15
b_4 = 60(1+60/12) = 60(6) = 360.
b_4 = 60(1+60/12) = 60(6) = 360.
YellowMarker16119:31:19
since the b sequence is so similar to the a, we should look for factorials there 2
since the b sequence is so similar to the a, we should look for factorials there 2
DPatrick19:31:22
Absolutely.
Absolutely.
DPatrick19:31:30
We see the same factorial-like pattern.
We see the same factorial-like pattern.
delian19:31:34
b_n = (n+2)! /2
b_n = (n+2)! /2
karatemagic719:31:34
(n+2)!/2??
(n+2)!/2??
dingzhou19:31:41
b_n=(n+2)!/2
b_n=(n+2)!/2
DPatrick19:31:45
We get b_n = (1/2)(n+2)!.
We get b_n = (1/2)(n+2)!.
DPatrick19:32:13
The fact that we're multiplying by (n+2) in every computation of b_n is the clue to look at (n+2)!.
The fact that we're multiplying by (n+2) in every computation of b_n is the clue to look at (n+2)!.
DPatrick19:32:25
It works for n=0,1 and the same proof for the a's shows this formula works for the b's.
It works for n=0,1 and the same proof for the a's shows this formula works for the b's.
DPatrick19:32:38
So now we've got formulas.
So now we've got formulas.
miller4math19:32:44
evaluate for 32: 33*34/2
evaluate for 32: 33*34/2
ra524919:33:01
so it is ((34)(33)(32!)/2)/(32!) = 17*33
so it is ((34)(33)(32!)/2)/(32!) = 17*33
DPatrick19:33:04
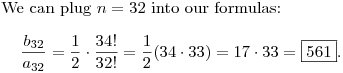
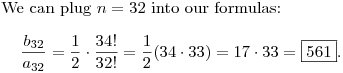
DPatrick19:33:32
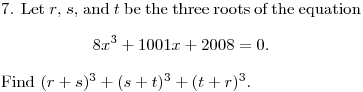
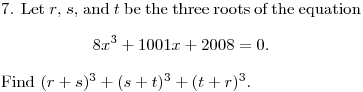
DPatrick19:33:35
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-79480990.gif
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-79480990.gif
delian19:34:13
Use the viet formulas!!
Use the viet formulas!!
DPatrick19:34:18
We have a symmetric equation for the roots...this looks like a job for Vieta!
We have a symmetric equation for the roots...this looks like a job for Vieta!
infinity4ever19:34:27
sum of roots = 0
sum of roots = 0
asdf419:34:27
r+t+s=0
r+t+s=0
DPatrick19:34:39
Right...the key observation is that there is no x^2 term. So the sum of the roots is 0.
Right...the key observation is that there is no x^2 term. So the sum of the roots is 0.
frodo19:34:52
r+s=-t s+t=-r t+r=-s
r+s=-t s+t=-r t+r=-s
ra524919:34:52
r+s+t=0 so it is actually -(r^3+s^3+t^3)
r+s+t=0 so it is actually -(r^3+s^3+t^3)
DPatrick19:35:05
Right...this means we can replace r+s with -t, since r+s+t = 0.
Right...this means we can replace r+s with -t, since r+s+t = 0.
DPatrick19:35:11
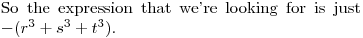
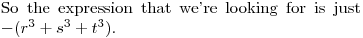
kops72319:35:37
now we just take (r+s+t)^3=0 and examine it
now we just take (r+s+t)^3=0 and examine it
frodo19:35:37
cube the sum of roots now
cube the sum of roots now
DPatrick19:35:43
That's one possibility.
That's one possibility.
DPatrick19:35:53
However, there is a somewhat simpler way to finish from here.
However, there is a somewhat simpler way to finish from here.
miller4math19:35:59
plug back into equation
plug back into equation
gemihmi19:36:03
can also plug r, s, and t in and sum these three equations
can also plug r, s, and t in and sum these three equations
DPatrick19:36:09
The easiest way to get the sum of the cubes is to just plug them in to the original equation.
The easiest way to get the sum of the cubes is to just plug them in to the original equation.
DPatrick19:36:19
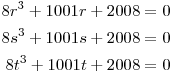
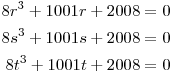
DPatrick19:36:41
When we add these, the cubic terms sum to -8 times what we want.
When we add these, the cubic terms sum to -8 times what we want.
DPatrick19:36:56
The linear terms go away, since r+s+t = 0.
The linear terms go away, since r+s+t = 0.
DPatrick19:37:20
So we have -8x + 3(2008) = 0, where x is our answer.
So we have -8x + 3(2008) = 0, where x is our answer.
kops72319:37:36
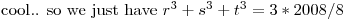
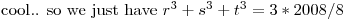
infinity4ever19:37:38
753
753
frodo19:37:41
x=753
x=753
DPatrick19:37:46
That's it.
That's it.
DPatrick19:37:59
Hence x = 3(2008)/8 = 3(251) = 753.
Hence x = 3(2008)/8 = 3(251) = 753.
DPatrick19:38:29
If you didn't see the clever way, the more standard way to approach it is to expand (x+y+z)^3.
If you didn't see the clever way, the more standard way to approach it is to expand (x+y+z)^3.
DPatrick19:38:51
It's a bit longer but it comes out the same.
It's a bit longer but it comes out the same.
DPatrick19:39:02
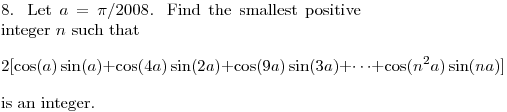
DPatrick19:39:05
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-146432974.gif
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-146432974.gif
stupidityismygam19:39:31
screams product-tosum
screams product-tosum
unimpossible19:39:31
First thing you do is product to sum
First thing you do is product to sum
DPatrick19:39:42
Certainly one idea is to use a "product-to-sum" formula on the terms.
Certainly one idea is to use a "product-to-sum" formula on the terms.
DPatrick19:39:49
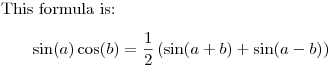
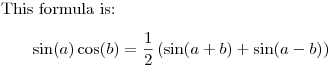
DPatrick19:40:00
(If you don't have this formula memorized -- and I don't! -- you can easily re-derive it. You know that it has to have a sin(a+b) in there somewhere to get a sin(a)cos(b) term out, and then the sin(a-b) will cancel the sin(b)cos(a) term that also comes out.)
(If you don't have this formula memorized -- and I don't! -- you can easily re-derive it. You know that it has to have a sin(a+b) in there somewhere to get a sin(a)cos(b) term out, and then the sin(a-b) will cancel the sin(b)cos(a) term that also comes out.)
miller4math19:40:22
take out the 1/2
take out the 1/2
DPatrick19:40:33
Yes, conveniently the 2 on the outside will cancel with the 1/2 in the product-to-sum formula.
Yes, conveniently the 2 on the outside will cancel with the 1/2 in the product-to-sum formula.
DPatrick19:40:43
What's left of each term will look like:
What's left of each term will look like:
DPatrick19:40:49
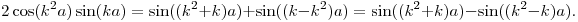
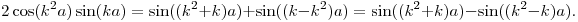
DPatrick19:41:06
oops, that's a little wider than I was hoping...let me reformat it.
oops, that's a little wider than I was hoping...let me reformat it.
DPatrick19:41:24
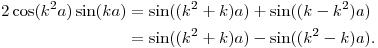
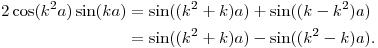
asdf419:41:44
telescoping!
telescoping!
unimpossible19:41:44
telescope
telescope
kops72319:41:44
we have a sorta telescope now... at the very least any terms adjacent in the original summation now have a term in common
we have a sorta telescope now... at the very least any terms adjacent in the original summation now have a term in common
DPatrick19:41:48
The sum telescopes!
The sum telescopes!
DPatrick19:42:08
Note that (k+1)^2 - (k+1) = k^2 + 2k + 1 - k - 1 = k^2 + k, so the "+" term for k cancels with the "-" term for k+1.
Note that (k+1)^2 - (k+1) = k^2 + 2k + 1 - k - 1 = k^2 + k, so the "+" term for k cancels with the "-" term for k+1.
DPatrick19:42:40
Thus the whole sum just has the "+" term for k=n and the "-" term for k=1.
Thus the whole sum just has the "+" term for k=n and the "-" term for k=1.
frodo19:42:47
sin((n^2+n)a)
sin((n^2+n)a)
DPatrick19:42:53
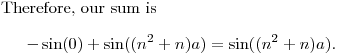
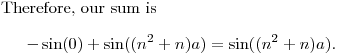
DPatrick19:43:03
We need the smallest positive integer n that makes this an integer.
We need the smallest positive integer n that makes this an integer.
unimpossible19:43:26
for it to be an integer, an(n+1) has to be a multiple of pi/2
for it to be an integer, an(n+1) has to be a multiple of pi/2
DPatrick19:43:41
Right. sin(x) is a integer if and only if x is a multiple of pi/2.
Right. sin(x) is a integer if and only if x is a multiple of pi/2.
DPatrick19:44:02
So we need (n^2+n)a to be a multiple of pi/2.
So we need (n^2+n)a to be a multiple of pi/2.
3468Yz19:44:12
n^2 + n is divisible by 1004
n^2 + n is divisible by 1004
DPatrick19:44:29
Exactly...since a = pi/2008, we need that n(n+1) is a multiple of 1004.
Exactly...since a = pi/2008, we need that n(n+1) is a multiple of 1004.
gemihmi19:44:39
so n or n+1 must be multiples of 251
so n or n+1 must be multiples of 251
YXYZI19:44:39
251 in prime
251 in prime
frodo19:44:39
251*2^2
251*2^2
DPatrick19:44:57
Right. 1004 = 4*251, and 251 is prime, so in particular either n or n+1 must be a multiple of 251.
Right. 1004 = 4*251, and 251 is prime, so in particular either n or n+1 must be a multiple of 251.
asdf419:45:24
cant be 250 because it wont be multiple of 4
cant be 250 because it wont be multiple of 4
DPatrick19:45:43
n=250 might work, but 250*251 is not a multiple of 1004 since it's not a multiple of 4.
n=250 might work, but 250*251 is not a multiple of 1004 since it's not a multiple of 4.
DPatrick19:45:58
The next n is 251. Indeed now 251*252 is a multiple of 1004 (since 252 is a multiple of 4).
The next n is 251. Indeed now 251*252 is a multiple of 1004 (since 252 is a multiple of 4).
DPatrick19:46:04
So the answer is 251.
So the answer is 251.
DPatrick19:46:22
An alternate solution is to use complex numbers. (This is also handy if you don't have all the trig formulas memorized.)
An alternate solution is to use complex numbers. (This is also handy if you don't have all the trig formulas memorized.)
DPatrick19:46:35
I'll just briefly sketch it and let you fill in the details.
I'll just briefly sketch it and let you fill in the details.
DPatrick19:46:44
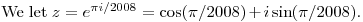
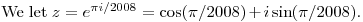
DPatrick19:46:54
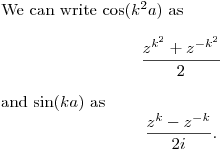
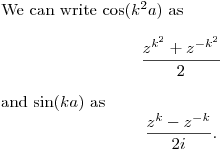
DPatrick19:47:06
DPatrick19:47:25
This sum telescopes in the same way that it did before, with the same result.
This sum telescopes in the same way that it did before, with the same result.
DPatrick19:47:40
It's actually the same solution as the one we did, but written in terms of complex numbers instead of trig.
It's actually the same solution as the one we did, but written in terms of complex numbers instead of trig.
DPatrick19:47:56
The only advantage the complex-numbers solution has is that you don't have to memorize or rederive the product-to-sum formula.
The only advantage the complex-numbers solution has is that you don't have to memorize or rederive the product-to-sum formula.
DPatrick19:48:07


DPatrick19:48:12
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-95613294.gif
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-95613294.gif
fzhang19:48:35
draw it
draw it
DPatrick19:48:49
Yes, let's sketch a picture of the first move:
Yes, let's sketch a picture of the first move:
DPatrick19:48:56
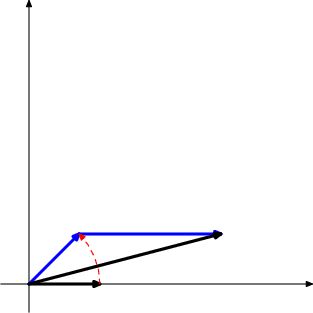

DPatrick19:48:57
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/d135b6adeb83bf292fab2b8a1ef829e5.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/d135b6adeb83bf292fab2b8a1ef829e5.png
DPatrick19:49:09
The horizontal black arrow points to the original point (5,0).
The horizontal black arrow points to the original point (5,0).
DPatrick19:49:18
The blue lines are the rotation of the original point, followed by the addition of (10,0). So the diagonal black arrow points to the point after 1 move.
The blue lines are the rotation of the original point, followed by the addition of (10,0). So the diagonal black arrow points to the point after 1 move.
karatemagic719:49:59
draw the second move
draw the second move
DPatrick19:50:02
Yeah, maybe it's not yet clear what's going on, so I drew one more "move":
Yeah, maybe it's not yet clear what's going on, so I drew one more "move":
DPatrick19:50:09
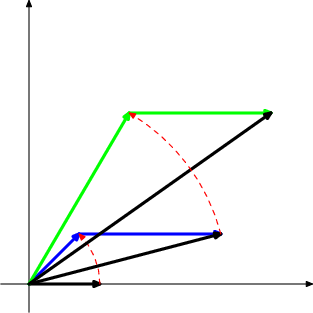

DPatrick19:50:10
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/1c676f18606156d160bd049faebe6f9c.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/1c676f18606156d160bd049faebe6f9c.png
DPatrick19:50:19
The green arrows are the rotation of the previous point and the addition of (10,0).
The green arrows are the rotation of the previous point and the addition of (10,0).
DPatrick19:50:33
But is there another way we could draw it?
But is there another way we could draw it?
DPatrick19:51:16
What if I draw the blue arrows rotated too?
What if I draw the blue arrows rotated too?
DPatrick19:51:24
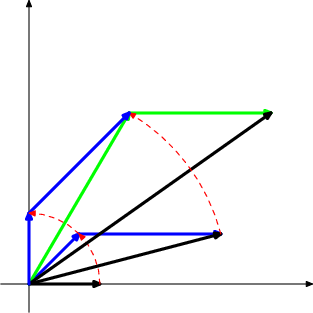

DPatrick19:51:25
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/c21be905973961ce3fb2546f95287deb.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/c21be905973961ce3fb2546f95287deb.png
DPatrick19:51:41
So the resulting point after 2 moves is a sum of:
- the original point rotated twice (90 degrees)
- plus the first (10,0) rotated once (45 degrees)
- plus the second (10,0)
So the resulting point after 2 moves is a sum of:
- the original point rotated twice (90 degrees)
- plus the first (10,0) rotated once (45 degrees)
- plus the second (10,0)
DPatrick19:52:25
The upshot is that we don't have to keep track of the point at the end of the black arrow. We can rotate all the components separately, then add them together!
The upshot is that we don't have to keep track of the point at the end of the black arrow. We can rotate all the components separately, then add them together!
fzhang19:52:35
apply it to 150 moves
apply it to 150 moves
DPatrick19:52:50
Right. The result after 150 moves is:
- the original point rotated 150 times
- plus the first (10,0) rotated 149 times
- plus the second (10,0) rotated 148 times
- plus the third (10,0) rotated 147 times
etc
- plus the last (10,0)
Right. The result after 150 moves is:
- the original point rotated 150 times
- plus the first (10,0) rotated 149 times
- plus the second (10,0) rotated 148 times
- plus the third (10,0) rotated 147 times
etc
- plus the last (10,0)
charles.du19:53:11
stuff cancels
stuff cancels
lowfatsourcreme19:53:13
but every 8 rotations is back to normal
but every 8 rotations is back to normal
DPatrick19:53:28
Many of them cancel out. Everything will cancel with the same thing rotated 4 additional times (4 rotations = 180 degrees).
Many of them cancel out. Everything will cancel with the same thing rotated 4 additional times (4 rotations = 180 degrees).
DPatrick19:53:42
So 149 will cancel with 145, 148 will cancel with 144, etc.
So 149 will cancel with 145, 148 will cancel with 144, etc.
DPatrick19:54:03
What's left is the original point rotated 150 times, plus a sum of (10,0) rotated 0,1,2,3,4 and 5 times.
What's left is the original point rotated 150 times, plus a sum of (10,0) rotated 0,1,2,3,4 and 5 times.
DPatrick19:54:18
We can see this final sum visually:
We can see this final sum visually:
DPatrick19:54:25
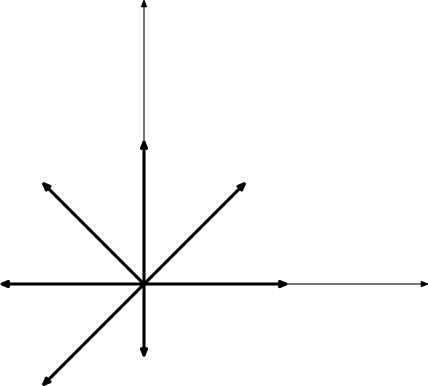

DPatrick19:54:27
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/309504f9adf8ec22b34a5a5ad11ad85a.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/309504f9adf8ec22b34a5a5ad11ad85a.png
DPatrick19:54:51
Actually even more cancels.
Actually even more cancels.
DPatrick19:55:09
All we have left are the vectors points up, up-and-to-the-left, and down.
All we have left are the vectors points up, up-and-to-the-left, and down.
DPatrick19:55:37
That's (0,10) + (-5*sqrt(2), 5*sqrt(2)) + (0,-5).
That's (0,10) + (-5*sqrt(2), 5*sqrt(2)) + (0,-5).
DPatrick19:55:53
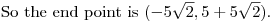
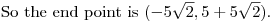
DPatrick19:56:11
The absolute values sum to 5 + 10*sqrt(2), whose floor is 5+14 = 019.
The absolute values sum to 5 + 10*sqrt(2), whose floor is 5+14 = 019.
YXYZI19:56:22
complex number
complex number
ra5249_219:56:22
complex numbers...
complex numbers...
stupidityismygam19:56:22
I thought that using cis (cos+isin) notation made it easier to visualize the rotations
I thought that using cis (cos+isin) notation made it easier to visualize the rotations
DPatrick19:56:32
You could also do it in terms of complex numbers instead of vectors in the plane.
You could also do it in terms of complex numbers instead of vectors in the plane.
DPatrick19:56:48
Rotating by 45 degrees is the same as multiplying by e^(i*pi/4).
Rotating by 45 degrees is the same as multiplying by e^(i*pi/4).
DPatrick19:57:10
You could also, if you didn't see a more clever way, crank it by hand.
You could also, if you didn't see a more clever way, crank it by hand.
DPatrick19:57:21
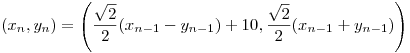
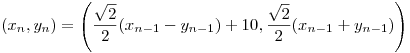
VLmath19:57:28
but that would take forever
but that would take forever
DPatrick19:57:46
Not necessarily...if you do the calculations carefully, you'll see that after 8 moves, you're back to where you started.
Not necessarily...if you do the calculations carefully, you'll see that after 8 moves, you're back to where you started.
DPatrick19:58:07
So 150 moves is the same as 6 moves, and from there you get your answer.
So 150 moves is the same as 6 moves, and from there you get your answer.
DPatrick19:58:18


DPatrick19:58:22
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-247799486.gif
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-247799486.gif
DPatrick19:58:27


DPatrick19:58:28
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/f4ff2f9f6b8f266e6ae1550b92eb85dd.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/f4ff2f9f6b8f266e6ae1550b92eb85dd.png
3468Yz19:58:52
Find all the possible single moves.
Find all the possible single moves.
charles.du19:58:52
find possible path lengths
find possible path lengths
samk19:59:02
list all of the lengths
list all of the lengths
DPatrick19:59:03
Right...we can determine how many possible different distances there are in the grid.
Right...we can determine how many possible different distances there are in the grid.
DPatrick19:59:20
All pairs of points are either 0,1,2,3 apart in the horizontal direction and 0,1,2,3 apart in the vertical direction.
All pairs of points are either 0,1,2,3 apart in the horizontal direction and 0,1,2,3 apart in the vertical direction.
DPatrick19:59:42
So the possible {horizontal, vertical} distances are:
{0,1}, {0,2}, {0,3}, {1,1}, {1,2}, {1,3}, {2,2}, {2,3}, {3,3}.
So the possible {horizontal, vertical} distances are:
{0,1}, {0,2}, {0,3}, {1,1}, {1,2}, {1,3}, {2,2}, {2,3}, {3,3}.
infinity4ever20:00:05
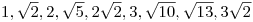
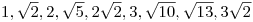
mathgeek200620:00:05
There are 9 different distances--
1, sqrt2, 2, sqrt(5), 2sqrt(2), sqrt(10) 3, sqrt(13), 3sqrt(2)
There are 9 different distances--
1, sqrt2, 2, sqrt(5), 2sqrt(2), sqrt(10) 3, sqrt(13), 3sqrt(2)
3468Yz20:00:05
1, sqrt(2), 2, sqrt(5), sqrt(8), 3, sqrt(10), sqrt(13), sqrt(18) are the distances.
1, sqrt(2), 2, sqrt(5), sqrt(8), 3, sqrt(10), sqrt(13), sqrt(18) are the distances.
DPatrick20:00:15
We need the distances (since we need them sorted in strictly increasing order), so we can make a table:
We need the distances (since we need them sorted in strictly increasing order), so we can make a table:
DPatrick20:00:21


DPatrick20:00:28
The "Move" column is the number of units moved horizontally and vertically, in either order.
The "Move" column is the number of units moved horizontally and vertically, in either order.
YXYZI20:00:51
m=10
m=10
mathgeek200620:00:51
so 10 points is the maximum (9 lines)
so 10 points is the maximum (9 lines)
DPatrick20:01:15
All of these distances are different, so a 10-point path is theoretically possible. (10 points means 9 segments, each of a different length.)
All of these distances are different, so a 10-point path is theoretically possible. (10 points means 9 segments, each of a different length.)
3468Yz20:01:25
See if all the moves can be made on the grid by working backwards.
See if all the moves can be made on the grid by working backwards.
samk20:01:25
you can draw it starting from largest line to smallest
you can draw it starting from largest line to smallest
DPatrick20:01:39
Right. One principal of counting is to deal with the most restrictive condition first, if possible. Here, those long moves at the end of the path are the most restrictive moves.
Right. One principal of counting is to deal with the most restrictive condition first, if possible. Here, those long moves at the end of the path are the most restrictive moves.
DPatrick20:01:53
So let's count the paths in reverse. In other words, let's count shrinking paths: paths of distinct points in which the distances are strictly decreasing.
So let's count the paths in reverse. In other words, let's count shrinking paths: paths of distinct points in which the distances are strictly decreasing.
karatemagic720:02:04
the (3,3) has to go from corner to corner
the (3,3) has to go from corner to corner
3468Yz20:02:04
The last line goes from corner to corner,
The last line goes from corner to corner,
samk20:02:08
there are 4 possible ways to position the 3x3 line
there are 4 possible ways to position the 3x3 line
DPatrick20:02:13
The first move {3,3} is across a diagonal of the grid, so the path must start at one corner.
The first move {3,3} is across a diagonal of the grid, so the path must start at one corner.
DPatrick20:02:18
By symmetry, it doesn't matter which one, but let's keep track that we have 4 choices at this step.
By symmetry, it doesn't matter which one, but let's keep track that we have 4 choices at this step.
DPatrick20:02:27

DPatrick20:02:28
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/bde0ddca741387309e023ac9917724c0.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/bde0ddca741387309e023ac9917724c0.png
DPatrick20:02:43
(I'll label the points "1", "2" in the order that we use them in our path. Drawing lines is really messy.)
(I'll label the points "1", "2" in the order that we use them in our path. Drawing lines is really messy.)
asdf420:03:08
the second step is arbitrary, because its symmetric, so 2 possibilities there?
the second step is arbitrary, because its symmetric, so 2 possibilities there?
samk20:03:08
two choices for next one
two choices for next one
3468Yz20:03:08
Then, point 3 is 1 away from point 1.
Then, point 3 is 1 away from point 1.
VLmath20:03:08
So there are 2 choices from here
So there are 2 choices from here
DPatrick20:03:15
We have to do a {2,3} move, so it has to be the point either immediately right of 1 or immediately below 1.
We have to do a {2,3} move, so it has to be the point either immediately right of 1 or immediately below 1.
DPatrick20:03:34
Again, by symmetry, it doesn't matter which, so let's pick one arbitrarily, but remember that we have 2 choices. That's 4*2 = 8 choices so far.
Again, by symmetry, it doesn't matter which, so let's pick one arbitrarily, but remember that we have 2 choices. That's 4*2 = 8 choices so far.
DPatrick20:04:01
Oops...I forgot the picture for this step. Let's put "3" to the right of "1", and I'll update the picture again after the next step.
Oops...I forgot the picture for this step. Let's put "3" to the right of "1", and I'll update the picture again after the next step.
DPatrick20:04:08
Where can "4" go?
Where can "4" go?
3468Yz20:04:23
Making the (3,1) move to the corner is disallowed because there will be no (3,0) move afterward.
Making the (3,1) move to the corner is disallowed because there will be no (3,0) move afterward.
DPatrick20:04:32
The next move is {1,3}, so we can go to either the lower-left corner or the point to the left of "2".
The next move is {1,3}, so we can go to either the lower-left corner or the point to the left of "2".
DPatrick20:04:40
But if we go to the corner, we can't make the next move after that, which is {0,3}, since those points are already occupied.
But if we go to the corner, we can't make the next move after that, which is {0,3}, since those points are already occupied.
DPatrick20:04:46
So we have to go to the point to the left of 2. This means the {0,3} move is straight up to the top:
So we have to go to the point to the left of 2. This means the {0,3} move is straight up to the top:
DPatrick20:04:53

DPatrick20:04:54
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/7e53902585bd7edc0689e4b03229fce6.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/7e53902585bd7edc0689e4b03229fce6.png
DPatrick20:05:17
Again, to recap, we have 8 choices thus far.
Again, to recap, we have 8 choices thus far.
VLmath20:05:25
and then {2,2} for 1 choice then?
and then {2,2} for 1 choice then?
samk20:05:25
one possibility for next step
one possibility for next step
DPatrick20:05:38
The next move {2,2} is fixed. The {1,2} and {0,2} and {1,1} moves after that are fixed as well. I'll draw them all in:
The next move {2,2} is fixed. The {1,2} and {0,2} and {1,1} moves after that are fixed as well. I'll draw them all in:
DPatrick20:05:44

DPatrick20:05:47
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/1f06911a6a2a8f9398f6f0f13b2c4e54.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/1f06911a6a2a8f9398f6f0f13b2c4e54.png
DPatrick20:06:04
(You can check them yourself afterwards!)
(You can check them yourself afterwards!)
mathgeek200620:06:10
3 places to finish
3 places to finish
3468Yz20:06:10
There are three ways to put point 10.
There are three ways to put point 10.
samk20:06:10
3 choices for the last step
3 choices for the last step
charles.du20:06:13
3 choices for last
3 choices for last
DPatrick20:06:19
Finally, we see that there are 3 choices for the last {0,1} move: any of the points adjacent to "9" can be "10".
Finally, we see that there are 3 choices for the last {0,1} move: any of the points adjacent to "9" can be "10".
DPatrick20:06:29
So that's 3 choices at this step, and hence 8*3 = 24 choices overall.
So that's 3 choices at this step, and hence 8*3 = 24 choices overall.
VLmath20:06:40
so 240 is the answer then
so 240 is the answer then
delian20:06:40
so 240
so 240
miller4math20:06:40
and 24*10 = 240
and 24*10 = 240
DPatrick20:06:50
So there are 24 paths, and the path has 10 points, so the answer is 240.
So there are 24 paths, and the path has 10 points, so the answer is 240.
DPatrick20:07:10
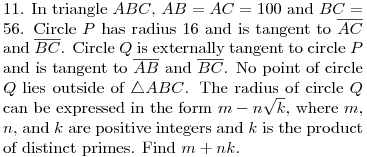
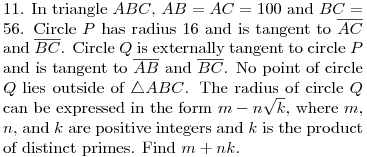
DPatrick20:07:14
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-56381230.gif
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-56381230.gif
VLmath20:07:29
diagram!
diagram!
asdf420:07:29
draw it
draw it
charles.du20:07:29
diagram
diagram
karatemagic720:07:29
draw a pic
draw a pic
DPatrick20:07:38
Of course we want to start with a diagram:
Of course we want to start with a diagram:
DPatrick20:07:47

DPatrick20:07:49
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/cd0ae57725a05fe2a1dc3ea91bc046ab.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/cd0ae57725a05fe2a1dc3ea91bc046ab.png
DPatrick20:08:05
People who have a *lot* of experience with plane geometry problem-solving may already recognize the important ratios in this problem. If you don't, though, how should we begin?
People who have a *lot* of experience with plane geometry problem-solving may already recognize the important ratios in this problem. If you don't, though, how should we begin?
ra5249_220:08:22
draw the height
draw the height
DPatrick20:08:32
Drop an altitude from A down to M (the midpoint of BC).
Drop an altitude from A down to M (the midpoint of BC).
DPatrick20:08:50
(Let's forget the circles for a moment, and learn what we can about ABC first.)
(Let's forget the circles for a moment, and learn what we can about ABC first.)
ra5249_220:08:58
7-24-25s
7-24-25s
infinity4ever20:08:58
this is twice a multiple of a 7-24-25 triangle
this is twice a multiple of a 7-24-25 triangle
asdf420:08:58
7-24-25 triangle
7-24-25 triangle
DPatrick20:09:17
Right. ABM is a 28-h-100 right triangle, where h = AM = the height of ABC.
Right. ABM is a 28-h-100 right triangle, where h = AM = the height of ABC.
DPatrick20:09:26
This is where it pays to know your basic Pythagorean triples. 28-h-100 is 4 times 7-24-25, so the height h=4*24 = 96.
This is where it pays to know your basic Pythagorean triples. 28-h-100 is 4 times 7-24-25, so the height h=4*24 = 96.
DPatrick20:09:35
(Or you could compute sqrt(100^2 - 28^2).)
(Or you could compute sqrt(100^2 - 28^2).)
DPatrick20:09:45
So the height of ABC is 96.
So the height of ABC is 96.
DPatrick20:10:12
Why is that useful?
Why is that useful?
samk20:10:46
heights are always useful
heights are always useful
DPatrick20:10:56
...well, for one thing, they let us compute areas.
...well, for one thing, they let us compute areas.
DPatrick20:11:09
The area of ABC is (96*56)/2 = 48*56.
The area of ABC is (96*56)/2 = 48*56.
DPatrick20:11:18
Why did I bother to do that?
Why did I bother to do that?
DPatrick20:11:29
How could areas possibly be relevant?
How could areas possibly be relevant?
karatemagic720:11:41
are of triangle =rs ?
are of triangle =rs ?
the future20:11:47
inradius?
inradius?
DPatrick20:11:54
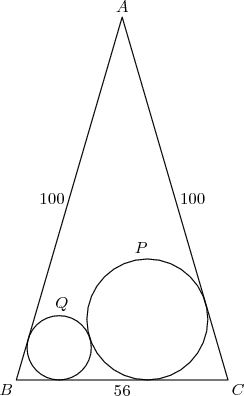
Aha! The area of ABC is also rs, where r is the radius of the inscribed circle of ABC and s is its semiperimeter.
Aha! The area of ABC is also rs, where r is the radius of the inscribed circle of ABC and s is its semiperimeter.
DPatrick20:12:02
Since s = 128, we have r = 48*56 / 128 = 21.
Since s = 128, we have r = 48*56 / 128 = 21.
DPatrick20:12:29
Now I can fill in a little more of the picture.
Now I can fill in a little more of the picture.
DPatrick20:12:38
Draw the angle bisectors from B and C. (I'm going to delete the top of the triangle from the picture, since it's not that important.)
Draw the angle bisectors from B and C. (I'm going to delete the top of the triangle from the picture, since it's not that important.)
DPatrick20:12:44

DPatrick20:12:45
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/25d245114bc9a7994016c2813a69867b.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/25d245114bc9a7994016c2813a69867b.png
DPatrick20:12:51
I've also labeled a few more points. P and Q are the centers of the circles, I is the incenter of the triangle, and M is the midpoint of BC.
I've also labeled a few more points. P and Q are the centers of the circles, I is the incenter of the triangle, and M is the midpoint of BC.
DPatrick20:12:59
We just determined that IM = 21.
We just determined that IM = 21.
charles.du20:13:28
why do the inradii go through q and p?
why do the inradii go through q and p?
DPatrick20:13:55
That's the key. P must lie on the angle bisector of C, since the distance from P to BC equals the distance from P to AC.
That's the key. P must lie on the angle bisector of C, since the distance from P to BC equals the distance from P to AC.
DPatrick20:14:28
What should I add to my picture now?
What should I add to my picture now?
VLmath20:14:51
can you draw a perpendicular line from center Q to line BC since there is a point of tangency?
can you draw a perpendicular line from center Q to line BC since there is a point of tangency?
frodo20:14:56
q and p's radii
q and p's radii
DPatrick20:15:09
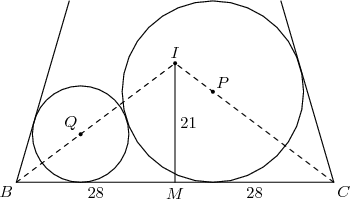
Yes, let's drop perpendicular lines from P and Q down to BC.
Yes, let's drop perpendicular lines from P and Q down to BC.
DPatrick20:15:18

DPatrick20:15:20
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/702e18e7e147a7902176dea1d59cf397.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/702e18e7e147a7902176dea1d59cf397.png
VLmath20:15:24
and then use similar triangles from there
and then use similar triangles from there
DPatrick20:15:31
Yes..similar triangles!
Yes..similar triangles!
DPatrick20:15:47
BIM and CIM are 21-28-35 triangles (7 times a 3-4-5 triangle).
BIM and CIM are 21-28-35 triangles (7 times a 3-4-5 triangle).
DPatrick20:16:18
So BQQ' and CPP' are also similar to 3-4-5 triangles. (The vertical heights are the "3" sides.)
So BQQ' and CPP' are also similar to 3-4-5 triangles. (The vertical heights are the "3" sides.)
DPatrick20:16:28
So what's CP'?
So what's CP'?
frodo20:17:04
P'C=64/3
P'C=64/3
karatemagic720:17:04
64/3
64/3
DPatrick20:17:17
We're given PP' = 16. CPP' is similar to 3-4-5.
We're given PP' = 16. CPP' is similar to 3-4-5.
DPatrick20:17:23
So CP' =(4/3)(16) = 64/3.
So CP' =(4/3)(16) = 64/3.
DPatrick20:17:34
QQ' is what we're trying to find, so let's call it x.
QQ' is what we're trying to find, so let's call it x.
DPatrick20:17:41
What's BQ'?
What's BQ'?
frodo20:18:25
4x/3
4x/3
DPatrick20:18:38
Right, same thing. BQQ' is similar to 3-4-5, so BQ' = (4/3)x.
Right, same thing. BQQ' is similar to 3-4-5, so BQ' = (4/3)x.
DPatrick20:18:49
And P'Q' = 56 - (64/3) - (4/3)x = (104-4x)/3.
And P'Q' = 56 - (64/3) - (4/3)x = (104-4x)/3.
DPatrick20:19:05
What haven't we used yet?
What haven't we used yet?
frodo20:19:28
PQ
PQ
gemihmi20:19:28
two circles are tangent
two circles are tangent
VLmath20:19:40
you can connect the radii
you can connect the radii
DPatrick20:19:41
We haven't used the fact that the two circles are tangent to each other.
We haven't used the fact that the two circles are tangent to each other.
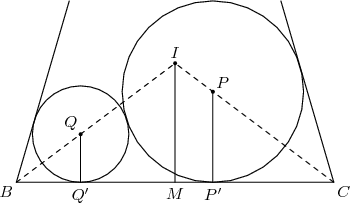
DPatrick20:19:48
This suggests drawing PQ.
This suggests drawing PQ.
DPatrick20:19:54
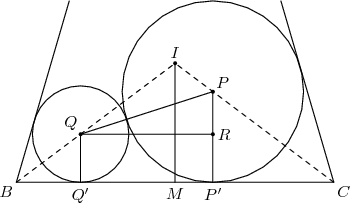

DPatrick20:19:55
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/c3cea4c69f20c779de2bcbc3776efb22.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/c3cea4c69f20c779de2bcbc3776efb22.png
DPatrick20:20:08
What's the length of PQ?
What's the length of PQ?
CreamCheesey20:20:23
16+x
16+x
charles.du20:20:23
16+x
16+x
DPatrick20:20:28
PQ = 16+x, the sum of the two radii.
PQ = 16+x, the sum of the two radii.
DPatrick20:20:32
How about PR?
How about PR?
frodo20:20:43
PR=16-x
PR=16-x
asdf420:20:43
16-x
16-x
delian20:20:43
16-x
16-x
DPatrick20:20:52
PR = 16-x, the difference of the two radii (since RP' = QQ' = x).
PR = 16-x, the difference of the two radii (since RP' = QQ' = x).
DPatrick20:21:01
And RQ = P'Q' = (104-4x)/3.
And RQ = P'Q' = (104-4x)/3.
VLmath20:21:07
use pythag
use pythag
DPatrick20:21:11
So we can apply the Pythagorean Theorem on PQR:
So we can apply the Pythagorean Theorem on PQR:
DPatrick20:21:17
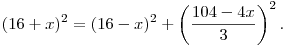
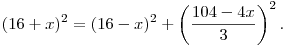
DPatrick20:21:39
We can use this to solve for x.
We can use this to solve for x.
VLmath20:21:41
some things will cancel out
some things will cancel out
DPatrick20:21:49
Right: it's easiest if we move the (16-x)^2 term to the left side first:
Right: it's easiest if we move the (16-x)^2 term to the left side first:
DPatrick20:21:56
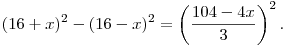
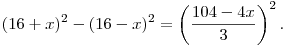
DPatrick20:22:02
The left side is now just 64x.
The left side is now just 64x.
frodo20:22:24
divide bu 4^2 now
divide bu 4^2 now
delian20:22:26
Multiply by 9 on both sides?
Multiply by 9 on both sides?
DPatrick20:22:36
Right, I'd do both: divide by 16 and multiply by 9:
Right, I'd do both: divide by 16 and multiply by 9:
DPatrick20:22:41
36x = (26 - x)^2.
36x = (26 - x)^2.
DPatrick20:22:58
Now we have to multiply it out I think:
Now we have to multiply it out I think:
DPatrick20:23:06
x^2 - 88x + 676 = 0.
x^2 - 88x + 676 = 0.
DPatrick20:23:15
(and move everything to one side too)
(and move everything to one side too)
frodo20:23:25
quadratic now
quadratic now
asdf420:23:29
quadratic formula...
quadratic formula...
DPatrick20:23:30
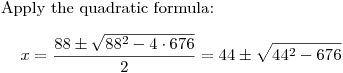
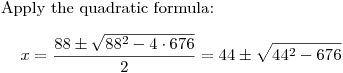
DPatrick20:24:28
It is plus or minus?
It is plus or minus?
asdf420:24:45
minus, otherwise too big
minus, otherwise too big
charles.du20:24:47
minus, plus is too big
minus, plus is too big
DPatrick20:25:00
Well, we know it has to be minus because the solution is in that form...
Well, we know it has to be minus because the solution is in that form...
DPatrick20:25:04
...but plus is indeed too big.
...but plus is indeed too big.
DPatrick20:25:18
Taking "+" gives a circle that is tangent to P on the other side, outside of the triangle.
Taking "+" gives a circle that is tangent to P on the other side, outside of the triangle.
DPatrick20:25:26
So the radius is 44 - 6*sqrt(35), and the answer is 44 + 6*35 = 254.
So the radius is 44 - 6*sqrt(35), and the answer is 44 + 6*35 = 254.
DPatrick20:25:40
This was a nice, though hard, plane geometry problem.
This was a nice, though hard, plane geometry problem.
DPatrick20:25:57


DPatrick20:26:02
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-112825166.gif
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-112825166.gif
DPatrick20:26:33
There are a number of ways to approach this.
There are a number of ways to approach this.
3468Yz20:26:49
Consider the 1/18, 2/17, 3/16,... cases.
Consider the 1/18, 2/17, 3/16,... cases.
DPatrick20:27:01
One way is casework based on the number of flags on each pole. It's a little messy but it's doable.
One way is casework based on the number of flags on each pole. It's a little messy but it's doable.
delian20:27:07
Instead of different flagpoles, line up the green flags and blue flags and poles are "barriers"
Instead of different flagpoles, line up the green flags and blue flags and poles are "barriers"
DPatrick20:27:17
This is pretty much how I looked at it.
This is pretty much how I looked at it.
DPatrick20:27:21
I thought of it as arranging 10 Bs, 9 Gs, and 1 X in a line, where the X indicates dividing point between the two flagpoles.
I thought of it as arranging 10 Bs, 9 Gs, and 1 X in a line, where the X indicates dividing point between the two flagpoles.
DPatrick20:27:37
The conditions are that the X can't be at either end, and no two G's can be next two each other.
The conditions are that the X can't be at either end, and no two G's can be next two each other.
DPatrick20:27:46
...next to each other.
...next to each other.
DPatrick20:28:04
How can we proceed from here?
How can we proceed from here?
3468Yz20:28:25
But two Gs can be next to each other if separated by the barrier.
But two Gs can be next to each other if separated by the barrier.
DPatrick20:28:37
But then they wouldn't be next to each other: my line would be GXG.
But then they wouldn't be next to each other: my line would be GXG.
delian20:29:03
So put a unknown barrier between every G
So put a unknown barrier between every G
DPatrick20:29:30
OK...we essentially have two choices, deal with the G's first or deal with the B's.
OK...we essentially have two choices, deal with the G's first or deal with the B's.
DPatrick20:29:45
What you suggest works, but then it's a little tricky dealing with the X.
What you suggest works, but then it's a little tricky dealing with the X.
DPatrick20:30:12
What I would do is first arrange the 10 B's and the X, then think of putting the G's in the slots between them.
What I would do is first arrange the 10 B's and the X, then think of putting the G's in the slots between them.
DPatrick20:30:34
But there are 2 cases, since the X at either end is a special case.
But there are 2 cases, since the X at either end is a special case.
DPatrick20:30:51
If we arrange 10 B's and the X such that the X is not at the end, how many choices do we have?
If we arrange 10 B's and the X such that the X is not at the end, how many choices do we have?
karatemagic720:31:16
9
9
samk20:31:16
9
9
DPatrick20:31:31
Right, there are 9 ways to arrange them. (We have to choose one of the 9 middle positions for the X.)
Right, there are 9 ways to arrange them. (We have to choose one of the 9 middle positions for the X.)
DPatrick20:31:41
Then in how many ways can we insert the nine G's?
Then in how many ways can we insert the nine G's?
YXYZI20:32:16
12C9
12C9
DPatrick20:32:34
Right. We have 12 slots into which we can place a G (the 10 slots between the B's and/or X, and two more at the end).
Right. We have 12 slots into which we can place a G (the 10 slots between the B's and/or X, and two more at the end).
DPatrick20:32:46
We have to place 9 G's, so we can do it is C(12,9) = C(12,3) ways.
We have to place 9 G's, so we can do it is C(12,9) = C(12,3) ways.
DPatrick20:33:00
So that's 9 * C(12,3) arrangements in this case.
So that's 9 * C(12,3) arrangements in this case.
DPatrick20:33:16
The other case is an arrangement of 10 B's and the X with the X at either end.
The other case is an arrangement of 10 B's and the X with the X at either end.
DPatrick20:33:21
There are of course 2 of these.
There are of course 2 of these.
DPatrick20:33:26
Now in how many ways can we insert the G's?
Now in how many ways can we insert the G's?
delian20:33:38
In this case, one of the Green flags is predetermined, must be at the end by the X
In this case, one of the Green flags is predetermined, must be at the end by the X
DPatrick20:33:47
Right. We have to stick one G in the slot outside of the X.
Right. We have to stick one G in the slot outside of the X.
DPatrick20:33:55
(Otherwise we'd have an empty flagpole.)
(Otherwise we'd have an empty flagpole.)
karatemagic720:34:04
11C8
11C8
delian20:34:07
11C8
11C8
DPatrick20:34:14
Yes, this leaves 11 slots in which to place the remaining 8 Gs. This can be done in C(11,8) = C(11,3) ways.
Yes, this leaves 11 slots in which to place the remaining 8 Gs. This can be done in C(11,8) = C(11,3) ways.
DPatrick20:34:22
So that's 2*C(11,8) arrangements from this case.
So that's 2*C(11,8) arrangements from this case.
DPatrick20:34:27
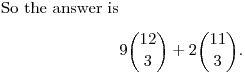
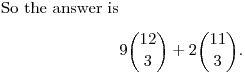
DPatrick20:34:54
You could carefully compute this out directly...
You could carefully compute this out directly...
DPatrick20:35:04
...or note that this is 9*12*11*10/6 + 2*11*10*9/6.
...or note that this is 9*12*11*10/6 + 2*11*10*9/6.
DPatrick20:35:16
9*10/6 = 15 is in each factor, so it's 12*11*15 + 2*11*15 = 14*11*15 = 210*11 = 2310.
9*10/6 = 15 is in each factor, so it's 12*11*15 + 2*11*15 = 14*11*15 = 210*11 = 2310.
delian20:35:33
so the remainder is 310
so the remainder is 310
DPatrick20:35:34
Dividing by 1000 leaves a remainder of 310.
Dividing by 1000 leaves a remainder of 310.
DPatrick20:35:57
DPatrick20:36:04
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-197358910.gif
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-197358910.gif
karatemagic720:36:11
draw a pic
draw a pic
DPatrick20:36:17
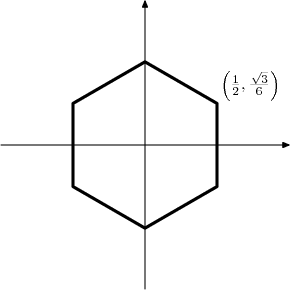
First let's make a sketch. Note that the vertical sides of the hexagon are at distance 1/2 from the imaginary (y) axis.
First let's make a sketch. Note that the vertical sides of the hexagon are at distance 1/2 from the imaginary (y) axis.
DPatrick20:36:26

DPatrick20:36:27
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/a797f3eb770642a3f25b1ed201559d5c.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/a797f3eb770642a3f25b1ed201559d5c.png
DPatrick20:36:40
Note that the indicated vertex of the hexagon corresponds to the complex number 1/2 + (sqrt(3)/6)i, and that the distance from the center to each vertex is sqrt(3)/3.
Note that the indicated vertex of the hexagon corresponds to the complex number 1/2 + (sqrt(3)/6)i, and that the distance from the center to each vertex is sqrt(3)/3.
DPatrick20:37:10
Now, if you know what the word inversion means (in terms of geometry), you have a huge advantage in this problem.
Now, if you know what the word inversion means (in terms of geometry), you have a huge advantage in this problem.
DPatrick20:37:18
But if you don't, it's still approachable.
But if you don't, it's still approachable.
sbk2017120:37:33
what does it mean
what does it mean
DPatrick20:37:43
It pretty much means doing what we're about to do.
It pretty much means doing what we're about to do.
DPatrick20:37:51
The advantage is that if you've done it before, you can save a lot of time.
The advantage is that if you've done it before, you can save a lot of time.
DPatrick20:38:11
Let's just focus on what 1/z does to the right-most vertical side, since that seems like the easiest to work with.
Let's just focus on what 1/z does to the right-most vertical side, since that seems like the easiest to work with.
DPatrick20:38:18
What's the easiest point to worry about first?
What's the easiest point to worry about first?
3468Yz20:38:38
The x-intercept
The x-intercept
DPatrick20:38:48
Right: the midpoint of the right side is easy.
Right: the midpoint of the right side is easy.
DPatrick20:39:03
It's the real number 1/2 on the complex plane.
It's the real number 1/2 on the complex plane.
DPatrick20:39:08
So 1/(1/2) = 2.
So 1/(1/2) = 2.
DPatrick20:39:21
So the point (1/2,0) gets mapped to the point (2,0) when we do 1/z.
So the point (1/2,0) gets mapped to the point (2,0) when we do 1/z.
karatemagic720:39:30
the vertexes
the vertexes
DPatrick20:39:37
Next we'll look at the vertices.
Next we'll look at the vertices.
DPatrick20:39:48
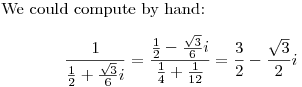
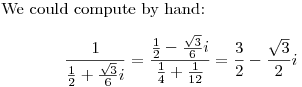
DPatrick20:40:06
(I skipped the computational details to save a little time.)
(I skipped the computational details to save a little time.)
DPatrick20:40:48
So the labeled point (in my original picture) goes to the point (3/2,-sqrt(3)/2) on the plane. Note that this point is 3 times the other vertex.
So the labeled point (in my original picture) goes to the point (3/2,-sqrt(3)/2) on the plane. Note that this point is 3 times the other vertex.
DPatrick20:41:12
Here's a picture that gives some of the answer away:
Here's a picture that gives some of the answer away:
DPatrick20:41:20
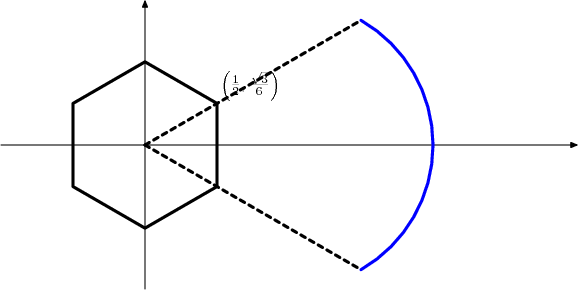

DPatrick20:41:21
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/eb26c7874cdc3f78adda08fc9e3c99c0.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/eb26c7874cdc3f78adda08fc9e3c99c0.png
DPatrick20:41:47
The upper right vertex gets mapped to the point in the far lower-right (where the mysterious blue arc that I've drawn hits the dotted line).
The upper right vertex gets mapped to the point in the far lower-right (where the mysterious blue arc that I've drawn hits the dotted line).
DPatrick20:42:03
And the lower-right vertex goes to the far upper-right point.
And the lower-right vertex goes to the far upper-right point.
sbk2017120:42:08
so you form a circle?
so you form a circle?
DPatrick20:42:41
Yes: I've given the answer away by drawing a circular arc. This is where the people who know "inversion" have their big advantage--they know it's a circle right away.
Yes: I've given the answer away by drawing a circular arc. This is where the people who know "inversion" have their big advantage--they know it's a circle right away.
panjia12320:42:47
it looks like six sectors that don't form a circle
it looks like six sectors that don't form a circle
karatemagic720:42:48
wheres the center?
wheres the center?
DPatrick20:43:14
To answer these questions, we can look at an arbitrary point on the right side of the original hexagon.
To answer these questions, we can look at an arbitrary point on the right side of the original hexagon.
DPatrick20:43:22
Every point on the vertical line is 1/2 + yi for some y.
Every point on the vertical line is 1/2 + yi for some y.
DPatrick20:43:30
So let's take its inverse:
So let's take its inverse:
DPatrick20:43:36
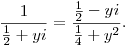
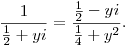
DPatrick20:43:46
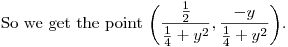
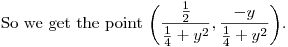
DPatrick20:43:54
Ick...let's call it (u,v) instead.
Ick...let's call it (u,v) instead.
DPatrick20:44:06
We want to find an equation relating u and v.
We want to find an equation relating u and v.
DPatrick20:44:34
We'd like to get rid of the ugly denominators, so we can take the ratio to cancel them. We see that v/u = -2y.
We'd like to get rid of the ugly denominators, so we can take the ratio to cancel them. We see that v/u = -2y.
DPatrick20:44:50
So y = -v/2u, and we can substitute this into the equation for u.
So y = -v/2u, and we can substitute this into the equation for u.
DPatrick20:45:02
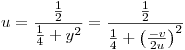
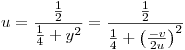
DPatrick20:45:20
(I know I'm doing this fast...you can go back and check the details later at your own pace.)
(I know I'm doing this fast...you can go back and check the details later at your own pace.)
DPatrick20:45:43
We'll clean this up a little and clear some denominators on the right side by multiplying top and bottom by 4u^2:
We'll clean this up a little and clear some denominators on the right side by multiplying top and bottom by 4u^2:
DPatrick20:45:50
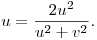
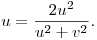
DPatrick20:46:15
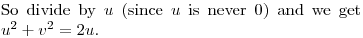
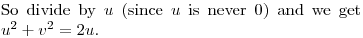
DPatrick20:46:31
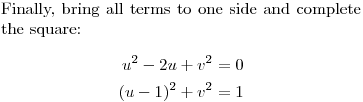
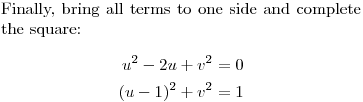
DPatrick20:46:41
So it's a circle with center (1,0) and radius 1.
So it's a circle with center (1,0) and radius 1.
DPatrick20:46:54
I've just given you a crash course in inversion! (A really crash course.)
I've just given you a crash course in inversion! (A really crash course.)
DPatrick20:47:10
Let's revisit our picture:
Let's revisit our picture:
DPatrick20:47:18
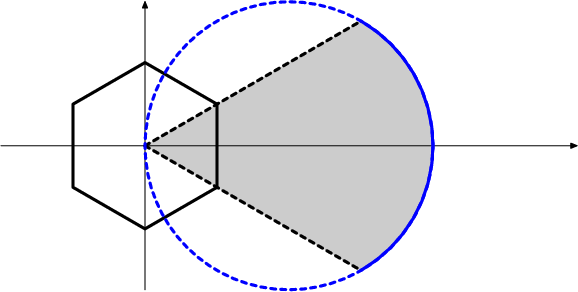

DPatrick20:47:19
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/fb544d7dafdf102733eaadea44cab5c2.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/fb544d7dafdf102733eaadea44cab5c2.png
DPatrick20:47:28
The shaded area is 1/6 of the region S that we need to compute.
The shaded area is 1/6 of the region S that we need to compute.
DPatrick20:47:48
(because, by symmetry, the same thing works on the other 5 sides too)
(because, by symmetry, the same thing works on the other 5 sides too)
DPatrick20:47:55
How do we compute its area?
How do we compute its area?
delian20:48:24
Equilateral triangle + cirle sector?
Equilateral triangle + cirle sector?
DPatrick20:48:33
Right, we divide it into a triangle and a segment of our circle:
Right, we divide it into a triangle and a segment of our circle:
DPatrick20:48:43
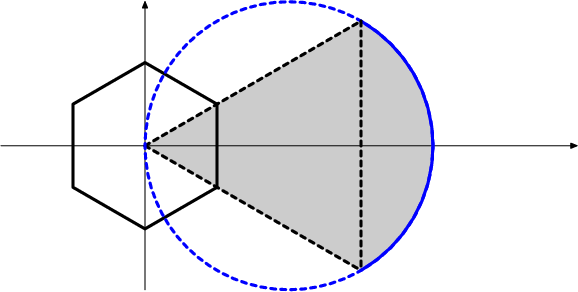

DPatrick20:48:46
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/471d0bab6f83eb179251f3bf2b089d30.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/471d0bab6f83eb179251f3bf2b089d30.png
delian20:49:11
Is it equilateral though?
Is it equilateral though?
DPatrick20:49:27
Yes: the central angle is 60 degrees. (But it's good to check!)
Yes: the central angle is 60 degrees. (But it's good to check!)
DPatrick20:49:37
The blue circle has radius 1.
The blue circle has radius 1.
DPatrick20:49:45
So the triangle has side length sqrt(3).
So the triangle has side length sqrt(3).
DPatrick20:49:51
So it has area 3*sqrt(3)/4.
So it has area 3*sqrt(3)/4.
DPatrick20:50:03
Now for the segment.
Now for the segment.
DPatrick20:50:14
(which is the part to the right of the vertical dashed line)
(which is the part to the right of the vertical dashed line)
panjia123_220:50:22
draw radii
draw radii
delian20:50:34
it is 1/3( Circle-Triangle)
it is 1/3( Circle-Triangle)
DPatrick20:50:37
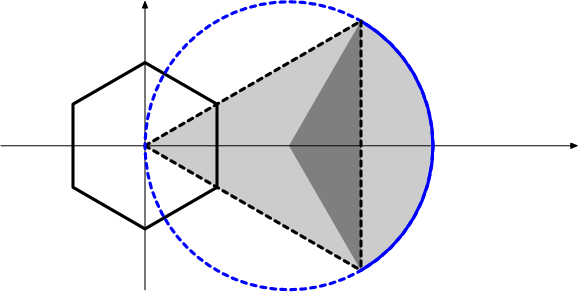

DPatrick20:50:38
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/aa6066bdbec8a673d20d50218518e3f6.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/aa6066bdbec8a673d20d50218518e3f6.png
DPatrick20:50:55
Right. The segment is 1/3 of the circle minus the area of the dark triangle.
Right. The segment is 1/3 of the circle minus the area of the dark triangle.
DPatrick20:51:10
This dark triangle has height 1/2 and base sqrt(3), so it has area sqrt(3)/4.
This dark triangle has height 1/2 and base sqrt(3), so it has area sqrt(3)/4.
karatemagic720:51:21
pi/3-rt(3)/4
pi/3-rt(3)/4
DPatrick20:51:26
So the area of the segment is pi/3 - sqrt(3)/4.
So the area of the segment is pi/3 - sqrt(3)/4.
DPatrick20:51:35
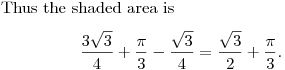
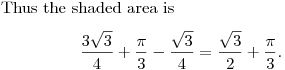
charles.du20:51:49
add and multiply by 6
add and multiply by 6
karatemagic720:51:51
multiply by 6
multiply by 6
DPatrick20:51:56
We have 6 equal areas composing S, so the area of S is:
We have 6 equal areas composing S, so the area of S is:
DPatrick20:52:00
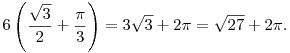
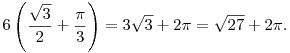
DPatrick20:52:09
Thus the answer is 27 + 2 = 029.
Thus the answer is 27 + 2 = 029.
DPatrick20:52:44
Inversion is a fascinating area of geometry if you care to study it further.
Inversion is a fascinating area of geometry if you care to study it further.
DPatrick20:52:58
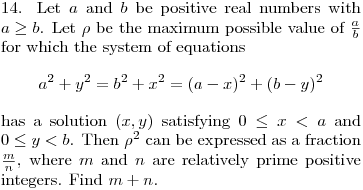
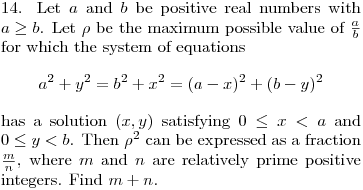
DPatrick20:53:03
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-163996606.gif
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-163996606.gif
DPatrick20:54:01
Anything of the form (blah)^2 + (blah)^2, especially a lot of them and especially something looking like that 3rd quantity in our equation, should lead you to consider a geometric interpretation in terms of distance.
Anything of the form (blah)^2 + (blah)^2, especially a lot of them and especially something looking like that 3rd quantity in our equation, should lead you to consider a geometric interpretation in terms of distance.
ra5249_220:54:18
distance to points?
distance to points?
DPatrick20:54:32
Absolutely. How can we represent the above system geometrically?
Absolutely. How can we represent the above system geometrically?
DPatrick20:55:16
a^2 + y^2 is the distance from the point (a,y) to the origin. (They even used x and y as a clue!)
a^2 + y^2 is the distance from the point (a,y) to the origin. (They even used x and y as a clue!)
DPatrick20:55:27
b^2 + x^2 is the distance from the point (x,b) to the origin.
b^2 + x^2 is the distance from the point (x,b) to the origin.
DPatrick20:55:33
What's the third quantity?
What's the third quantity?
DPatrick20:55:46
(actually, I lied; they're the square of the distances)
(actually, I lied; they're the square of the distances)
delian20:55:54
The distance from one pint to the other
The distance from one pint to the other
ra5249_220:55:54
distance from (a,y) to (x, b)
distance from (a,y) to (x, b)
DPatrick20:56:06
Right, the 3rd quantity is the square of the distance from (a,y) to (x,b).
Right, the 3rd quantity is the square of the distance from (a,y) to (x,b).
karatemagic720:56:09
equilateral triangle
equilateral triangle
DPatrick20:56:11
Aha!
Aha!
DPatrick20:56:18
It is saying is that (a,y), (x,b), and (0,0) are the vertices of an equilateral triangle.
It is saying is that (a,y), (x,b), and (0,0) are the vertices of an equilateral triangle.
DPatrick20:56:51
So we want to maximize a/b given that these points are the vertices of an equilateral triangle and lie in the 1st quadrant.
So we want to maximize a/b given that these points are the vertices of an equilateral triangle and lie in the 1st quadrant.
delian20:57:08
Now we have to consider the restrictions?
Now we have to consider the restrictions?
delian20:57:40
x<a, and y<b
x<a, and y<b
DPatrick20:57:43
Well, the restrictions tell us that the points (except for (0,0)) are in the first quadrant (or on the positive axes)), and tell us which point is which.
Well, the restrictions tell us that the points (except for (0,0)) are in the first quadrant (or on the positive axes)), and tell us which point is which.
DPatrick20:58:05
Also, because everything scales, we might as well assume that the side length is 2. (I chose 2 rather than 1 so that the coordinates won't have fractions.)
Also, because everything scales, we might as well assume that the side length is 2. (I chose 2 rather than 1 so that the coordinates won't have fractions.)
DPatrick20:58:14
Let's look at the extreme case first: where one side of the triangle is on the x-axis.
Let's look at the extreme case first: where one side of the triangle is on the x-axis.
DPatrick20:58:20

DPatrick20:58:21
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/ab32ed07cdcadb6ca1da6d74fcf0bbdc.png
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/ab32ed07cdcadb6ca1da6d74fcf0bbdc.png
DPatrick20:58:29
If the side length is 2, what are the vertices?
If the side length is 2, what are the vertices?
VLmath20:59:02
(0,0), (2,0), and (1, sqrt(3))
(0,0), (2,0), and (1, sqrt(3))
karatemagic720:59:02
(0,0)(1,rt(3))(2,0)
(0,0)(1,rt(3))(2,0)
DPatrick20:59:12
Right, the vertices are (0,0), (2,0) and (1,sqrt(3)).
Right, the vertices are (0,0), (2,0) and (1,sqrt(3)).
DPatrick20:59:35
The x<a and y<b restrictions tell us that (2,0) is (a,y) and (1,sqrt(3)) is (x,b).
The x<a and y<b restrictions tell us that (2,0) is (a,y) and (1,sqrt(3)) is (x,b).
DPatrick20:59:45
So the ratio a/b is 2/sqrt(3) for this triangle.
So the ratio a/b is 2/sqrt(3) for this triangle.
VLmath21:00:03
but would this maximize the values?
but would this maximize the values?
DPatrick21:00:14
It turns out it does...let's see why.
It turns out it does...let's see why.
DPatrick21:00:42
Every other triangle we get is by taking this one and rotating it counterclockwise around (0,0).
Every other triangle we get is by taking this one and rotating it counterclockwise around (0,0).
DPatrick21:00:54
...because (0,0) is fixed but the other two points move.
...because (0,0) is fixed but the other two points move.
DPatrick21:01:07
But as we rotate, a decreases and b increases!
But as we rotate, a decreases and b increases!
DPatrick21:01:16
So a/b decreases as we rotate.
So a/b decreases as we rotate.
DPatrick21:01:29
This means that the triangle I drew above is indeed the maximum a/b.
This means that the triangle I drew above is indeed the maximum a/b.
delian21:01:36
so p = 4/3
so p = 4/3
sbk2017121:01:46
now we square the ratio?
now we square the ratio?
DPatrick21:01:49
That's p^2, which is what we want.
That's p^2, which is what we want.
DPatrick21:01:58
p^2 = 4/3, so the answer is 4+3 = 007.
p^2 = 4/3, so the answer is 4+3 = 007.
DPatrick21:02:21
This problem can be done algebraically, but the geometric solution is too pretty!
This problem can be done algebraically, but the geometric solution is too pretty!
DPatrick21:02:37
Whenever you see things like (a-x)^2 + (b-y)^2, it should suggest analytic geometry.
Whenever you see things like (a-x)^2 + (b-y)^2, it should suggest analytic geometry.
DPatrick21:02:58
Finally...
Finally...
DPatrick21:03:06


DPatrick21:03:13
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-121577342.gif
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-121577342.gif
DPatrick21:03:28
Before we work through a solution, let me first say that this is the hardest AIME problem that I've seen in a while.
Before we work through a solution, let me first say that this is the hardest AIME problem that I've seen in a while.
DPatrick21:03:44
It is possible to "brute force" this solution by assuming that the answer is less than 1000, and then doing some sort of reduction that limits the number of possibilities that you have to check. While this sort of thing is acceptable for the AIME, it's not a proof that no number greater than 1000 works.
It is possible to "brute force" this solution by assuming that the answer is less than 1000, and then doing some sort of reduction that limits the number of possibilities that you have to check. While this sort of thing is acceptable for the AIME, it's not a proof that no number greater than 1000 works.
DPatrick21:03:59
However, the solution I'm about to work through will indeed prove the highest possible integer.
However, the solution I'm about to work through will indeed prove the highest possible integer.
VLmath21:04:10
make equations
make equations
DPatrick21:04:19
We can start by writing equations for both conditions:
We can start by writing equations for both conditions:
DPatrick21:04:26
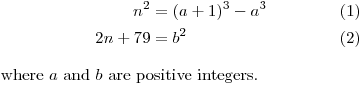
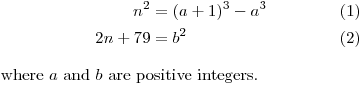
VLmath21:04:53
things cancel out
things cancel out
DPatrick21:05:06
We can at least cancel the cubic term in (1):
We can at least cancel the cubic term in (1):
DPatrick21:05:12
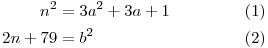
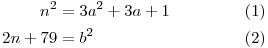
DPatrick21:05:30
Now there are 2 routes you can go...
Now there are 2 routes you can go...
knexpert21:05:35
form a pell equation with the first equation
form a pell equation with the first equation
DPatrick21:06:09
One is to use a somewhat technical number theory technique known as a Pell Equation. I'm not going to go into that here.
One is to use a somewhat technical number theory technique known as a Pell Equation. I'm not going to go into that here.
infinity4ever21:06:24
top is 3a^2+3a+1 so n^2=1 mod3
top is 3a^2+3a+1 so n^2=1 mod3
VLmath21:06:24
use guess and check for number 2?
use guess and check for number 2?
DPatrick21:06:39
Another one is to use a combination of reducing via various mods and/or guessing and checking.
Another one is to use a combination of reducing via various mods and/or guessing and checking.
DPatrick21:06:53
Both of these methods rely on the fact that you know ahead of time that the answer is less than 1000.
Both of these methods rely on the fact that you know ahead of time that the answer is less than 1000.
DPatrick21:07:11
You can make them work, since this is the AIME.
You can make them work, since this is the AIME.
DPatrick21:07:23
But I want to show a solution that also proves that the answer is less than 1000.
But I want to show a solution that also proves that the answer is less than 1000.
DPatrick21:07:37
Let's go back to our equations:
Let's go back to our equations:
DPatrick21:07:39
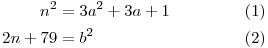
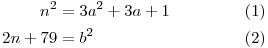
VLmath21:07:46
you just have two quadratic equations now
you just have two quadratic equations now
DPatrick21:08:04
Right, and (1) looks more like a "traditional" quadratic with a^2, a, and "constant" terms.
Right, and (1) looks more like a "traditional" quadratic with a^2, a, and "constant" terms.
DPatrick21:08:09
So let's solve it using the quadratic formula!
So let's solve it using the quadratic formula!
DPatrick21:08:17
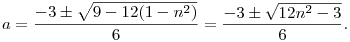
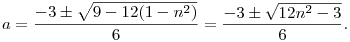
DPatrick21:08:26
What does this tell us?
What does this tell us?
VLmath21:08:40
12n^2-3 must be a square
12n^2-3 must be a square
DPatrick21:08:47
Right. In order for this to be an integer, we need that 12n^2 - 3 is a perfect square.
Right. In order for this to be an integer, we need that 12n^2 - 3 is a perfect square.
DPatrick21:09:06
But equation (2) from our system can also give us information about n^2.
But equation (2) from our system can also give us information about n^2.
DPatrick21:09:14
Let's rewrite it in terms of n^2:
Let's rewrite it in terms of n^2:
DPatrick21:09:22
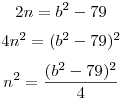
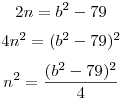
VLmath21:09:34
so we can equate these two somehow...
so we can equate these two somehow...
DPatrick21:09:41
Let's just plug this into our 12n^2 - 3 expression:
Let's just plug this into our 12n^2 - 3 expression:
DPatrick21:09:47
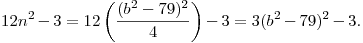
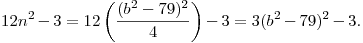
DPatrick21:09:58
Can we simplify this last expression?
Can we simplify this last expression?
delian21:10:02
factor out 3?
factor out 3?
DPatrick21:10:09
OK, and what's left? Can it be refactored?
OK, and what's left? Can it be refactored?
knexpert21:10:16
diff of squares
diff of squares
DPatrick21:10:19
Right!
Right!
DPatrick21:10:23
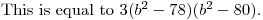
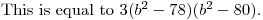
DPatrick21:10:32
We need this to be a perfect square.
We need this to be a perfect square.
DPatrick21:10:43
How can we analyze this?
How can we analyze this?
karatemagic721:10:58
either b^2-78 is divis by 3 or b^2-80 is divis by 3
either b^2-78 is divis by 3 or b^2-80 is divis by 3
DPatrick21:11:03
Right, which one is it?
Right, which one is it?
knexpert21:11:36
b^2-78
b^2-78
karatemagic721:11:36
b^2-78
b^2-78
knexpert21:11:41
use mods
use mods
DPatrick21:11:51
b^2 - 80 is either 1 or 2 mod 3, so it cannot be 3 times anything.
b^2 - 80 is either 1 or 2 mod 3, so it cannot be 3 times anything.
DPatrick21:11:57
So b^2 - 78 is the multiple of 3.
So b^2 - 78 is the multiple of 3.
DPatrick21:12:12
But more importantly...what does that tell us about b^2 - 80?
But more importantly...what does that tell us about b^2 - 80?
DPatrick21:12:27
The whole thing is a perfect square, remember.
The whole thing is a perfect square, remember.
Smartguy21:12:33
it is a perfect sq?
it is a perfect sq?
charles.du21:12:33
its a square
its a square
williamtz21:12:33
perfect square
perfect square
delian21:12:34
It is a square?
It is a square?
DPatrick21:12:46
Right. b^2-78 and b^2-80 are consecutive odd numbers.
Right. b^2-78 and b^2-80 are consecutive odd numbers.
DPatrick21:12:52
So they don't have any factors in common.
So they don't have any factors in common.
DPatrick21:13:14
If their product is a perfect square, then they are each perfect squares themselves (except for the extra 3 in b^2 - 78).
If their product is a perfect square, then they are each perfect squares themselves (except for the extra 3 in b^2 - 78).
DPatrick21:13:21
So in particular b^2 - 80 is a perfect square.
So in particular b^2 - 80 is a perfect square.
knexpert21:13:51
now its a diff of squares to solve in integers
now its a diff of squares to solve in integers
delian21:13:53
Well the difference betwwen to squares quickly becomes more than 80
Well the difference betwwen to squares quickly becomes more than 80
DPatrick21:13:55
Aha!
Aha!
DPatrick21:14:01
If b^2 - 80 = c^2, then b^2 - c^2 = 80, so (b+c)(b-c) = 80. So {b+c,b-c} is a factorization of 80, and b is the average of the two terms in the factorization.
If b^2 - 80 = c^2, then b^2 - c^2 = 80, so (b+c)(b-c) = 80. So {b+c,b-c} is a factorization of 80, and b is the average of the two terms in the factorization.
DPatrick21:14:22
This pretty severely limits what b can be.
This pretty severely limits what b can be.
VLmath21:14:28
factor 80
factor 80
karatemagic721:14:33
b is at most 21
b is at most 21
DPatrick21:14:42
It's now easy to check that {40,2} gives b=21 (and c=19) and this is the maximum possible value of b.
It's now easy to check that {40,2} gives b=21 (and c=19) and this is the maximum possible value of b.
DPatrick21:15:05
So that's the maximum possible value for b, and now we backtrack to get n.
So that's the maximum possible value for b, and now we backtrack to get n.
delian21:15:09
Plug back into original equation
Plug back into original equation
karatemagic721:15:11
plug into formula (2)
plug into formula (2)
DPatrick21:15:19
b=21 makes 2n = (21)^2 - 79 = 362, so n = 181.
b=21 makes 2n = (21)^2 - 79 = 362, so n = 181.
DPatrick21:15:41
We can double-check against our other conditions.
We can double-check against our other conditions.
DPatrick21:15:52
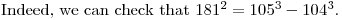
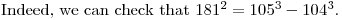
DPatrick21:15:58
So the answer is 181.
So the answer is 181.
DPatrick21:16:10
That's it for the Math Jam.
That's it for the Math Jam.
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.









