AIME Math Jam
Go back to the Math Jam ArchiveWe will review the problems from the 2005 AIME.
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.
Facilitator: Mathew Crawford
MCrawford (19:29:14)
2005 AIME Math Jam
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.
MCrawford (19:29:21)
The classroom is moderated meaning that students can type into the classroom, but only the moderators can choose a comment to drop into the classroom. This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
MCrawford (19:29:29)
Also, only moderators can enter into private chats with other people in the classroom. You can copy the contents of a private chat by clicking on the notebook icon on the private chat window and copying and pasting the contents into a file on your own computer.
MCrawford (19:29:45)
Finally, the virtual classroom is TeX enabled. TeX allows users to make nice equations and other math expressions. If you would like to learn how to write in TeX/LaTeX, click on the tab on the left side panel of our site and there is a tutorial and reference guide there.
MCrawford (19:29:58)
Using TeX in the virtual classroom is slightly different than using it on the message board or in a TeX editor. If anything you type up in a post that uses TeX then you must use a semicolon (;) to begin your post. For example, if you type
MCrawford (19:30:07)
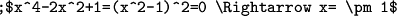
MCrawford (19:30:13)
This message will look like this when posted in the classroom:
MCrawford (19:30:24)
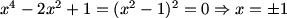
MCrawford (19:30:32)
Just remember, if your post uses TeX, use the semicolon (;) to begin your post!
aaronwysocki (19:30:03)
Quick question: What is the typical combined score you need to get to USAMO?
MCrawford (19:30:53)
That's impossible to know without knowing all the scores including the future scores on the Alternate AIME.
MCrawford (19:31:09)
Problem 1:
MCrawford (19:31:12)

MCrawford (19:31:26)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-227799305.gif
MCrawford (19:31:32)
Where might we begin with a problem such as this one?
towersfreak2006 (19:31:24)
draw a picture! :]
chesspro (19:31:38)
Picture.
justdudxit (19:31:43)
A diagram
sponge008 (19:31:41)
We should draw it...
MCrawford (19:32:01)
A good starting point is a diagram:
MCrawford (19:32:07)

MCrawford (19:32:20)
Now, how can we go about determining the area inside the larger circle and outside the smaller circles?
frodo (19:31:41)
The center of the small circles form a regular hexagon.
aerlinndan (19:32:08)
...and connect the centers of the small circles.
pika (19:31:39)
there's going to be a circle in the center with the same radius as the 6
ChrisChang (19:32:24)
looks like a 7th circle will fit in there
Geoffrey (19:32:29)
good to know that circles can tesselate like hexagons
winluo2 (19:32:29)
Draw radii
towersfreak2006 (19:32:30)
maybe connect all the centers of the little circles? it forms a regular hexagon
MCrawford (19:33:04)
In order to find the answer to this problem, we need to find the area (via the radius) of each smaller circle.
MCrawford (19:33:11)
It is sometimes helpful to connect the radii between tangent circles. In this case a very nice picture emerges:
conartist (19:32:43)
the center to two adjacent points of tangency creates a 60 degree angle
MCrawford (19:33:18)
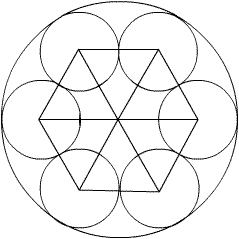
MCrawford (19:33:21)
What do we know about this hexagon?
Zyloch_2 (19:33:28)
regular
aerlinndan (19:33:30)
Those are six equilateral triangles
sponge008 (19:33:31)
It's regular.
mna851 (19:33:31)
its regular
SoccerBrainy40 (19:33:31)
It's a regular hexagon.
MCrawford (19:33:53)
Due to symmetry we know that the hexagon is regular.
xirtamax (19:33:43)
side of hexagon = diameter of small circle
pika (19:33:51)
The sides are the diameter of the circles
Zratonx (19:33:36)
its side is 2r
frodo (19:33:35)
The side is twice the radius
MCrawford (19:34:16)
We see that the radii of the circles are each half the length of a side of the hexagon. As the hexagon breaks up into 6 congruent equilateral triangle, this means the radii are each half the length of a side of each of the triangles.
vfiroiu (19:33:27)
radius of small circle=10
kky1638 (19:34:05)
Radius of one small circle is 1/3 of the big one!
Zratonx (19:34:20)
so the side+r=30 and the side=2r though 3r=30 and r=10
ChrisChang (19:32:41)
so we can determine the radius of the small circle = 30 / 3 = 10
MCrawford (19:34:51)
We can now see that the diameter of the larger circle is made up of 2 diameters of smaller circles plus two half lengths of the sides of the right triangles. In total, this makes 3 complete diameters of the smaller circles, so the radius of a smaller circle is 30/3 = 10.
MCrawford (19:34:55)
Now, what is the answer to our problem?
RC-7th_? (19:32:42)
Find the area of the large circle, then subtract the combined area of the smaller circles
kky1638 (19:35:11)
thus some of all 6 circle is 600pi
frodo (19:35:09)
30^2pi-6*10^2pi=300pi
Zratonx (19:35:15)
sp 900pi-600pi=300pi or 942
sponge008 (19:35:07)
942
MCrawford (19:35:42)
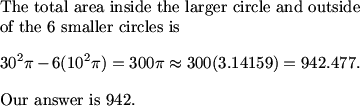
arkajit (19:31:58)
Since the circles are internaly tangent and congruent, they must each be inscribed within 360/60 = 60 degree sectors in the big circle, C. Then, we can see that we have a 30-60-90 triangle with short leg, little r of one of the circles, and hypotenuse (R - r) where R is the radius of the big circle, we can then find the area by subtracting 6 small circles from the big one.
MithsApprentice (19:34:09)
you can inscribe a circle inside the ring of 6 congruent circles that is congruent to each circle in the ring
MCrawford (19:36:05)
Some students might also be aware of the extension of this key symmetry to include a third smaller congruent circle within the ring of 6:
MCrawford (19:36:09)
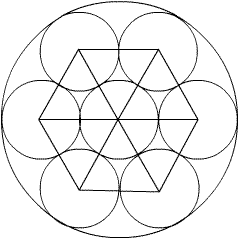
MCrawford (19:36:21)
This fact makes short work of the problem which goes to show how valuable experience can be in problem solving.
MCrawford (19:36:33)
These kinds of uses of symmetry and relationships between circles are covered in the AoPS Introduction to Geometry class.
mna851 (19:36:20)
On the test would you have to multiply that by 3.14 because no calculators are allowed
MCrawford (19:36:51)
Be careful, you have to express pi to more digits to be sure that your answer is correct on this one.
aerlinndan (19:36:34)
Why is that middle one smaller?
MCrawford (19:37:09)
It's not. Optical illusion.
blahblahblah (19:37:16)
You need 3 sig figs so take 4 sig figs in pi
origamimasterjared (19:36:09)
I used the fact that the angle bisectors/medians of the equilateral triangles cross at 1/3, ; \rightarrow 1\3*30=10 for the small circle radius.
MCrawford (19:37:39)
Let's take a look at problem 2:
MCrawford (19:37:44)

MCrawford (19:37:53)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-253122351.gif
MCrawford (19:38:00)
How might we start with this problem involving variable arithmetic series?
aerlinndan (19:38:12)
Create an explicit formula
rachel (19:38:06)
1+nk=2005
NightFlarer (19:38:09)
write it as 1, 1 + d, 1 + 2d, ...1+xd, so 1 + xd = 2005
pika (19:38:16)
2005=1+k, 1+2k, etc.
MCrawford (19:38:37)
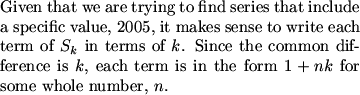
towersfreak2006 (19:38:26)
1, d+1, 2d+1,...,xd+1 or xd+1=2005
solafidefarms (19:38:17)
Subtract 1
chesspro (19:38:20)
1 + k + 2k + ... = 2005
k + 2k + ... = nk = 2004
conartist (19:38:12)
subtract 1 from each of the numbers in the sequence and you have multiples of k
MCrawford (19:39:13)
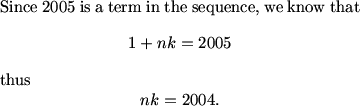
justdudxit (19:38:21)
k=factors of 2004
vfiroiu (19:38:27)
we need to find the factors of 2004
wild octagon (19:38:36)
factor 2004
flierdeke (19:38:38)
so nk = 2004.
rachel (19:38:39)
factors of 2004
smiley_2 (19:38:51)
Factor 2004, because 2004=nk
ChrisChang (19:38:52)
factors of 2004
MCrawford (19:39:39)
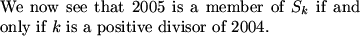
MCrawford (19:39:50)
Before we go on.
MCrawford (19:39:56)
I have a request.
MCrawford (19:40:14)
This Math Jam is getting very large. If you plan to post, please post succint ideas as concisely as possible.
MCrawford (19:40:29)
I will not have time to read all of the hundreds of posts.
MCrawford (19:40:32)
What is the number of positive divisors of 2004?
arkajit (19:39:37)
We know that to reach 2005, the sequence must increase in some integer amount of steps by 2004, thus we are looking for the number of divisors of 2004; we prime factorize and then we use the fact that p^n where p is prime and n is an integer will yield n + 1 divisors and we multiply by all such n - we have 2004 = 2^2 * 3 * 167; thus we have (2+1)(1+1)(1+1) = 12
conartist (19:39:37)
prime factorize 2004, raise powers +1 and multiply
vfiroiu (19:39:45)
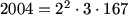
sponge008 (19:39:47)
2004=2^2*3*167
rachel (19:39:47)
3*2*2=12 factors
sponge008 (19:39:57)
So 3*2*2=12
frodo (19:39:57)
167*3*2^2=2004 There are 2*2*3=12 factors.
MCrawford (19:41:15)

MCrawford (19:41:28)
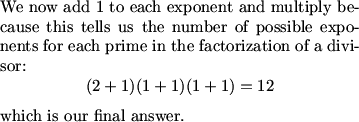
MCrawford (19:41:39)
There were two main keys to unlocking this problem. First, we needed to write the general form of a term of each arithmetic series. From there we did a tiny bit of manipulation to recognize the divisor counting problem within.
MCrawford (19:41:48)
Many kinds of divisor counting problems are covered in the AoPS Introduction to Number Theory class and basic algebraic manipulations of equations in integers will be covered in the Intermediate Number Theory class.
MCrawford (19:41:59)
Now, let's take a look at problem 3.
MCrawford (19:42:11)
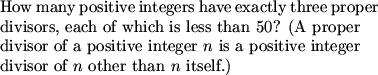
MCrawford (19:42:17)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-30557481.gif
MCrawford (19:42:29)
How can we begin with this problem?
krustyteklown (19:42:28)
3 proper divisors means 4 real divisors
Zratonx (19:42:44)
look for numbers with 4 factors
justdudxit (19:42:44)
The number actually has 4 factores
MCrawford (19:42:55)
First, we note that an integer with 3 proper divisors has a total of 4 divisors.
chesspro (19:42:34)
They're in the form:
x^3
x^1 * y^1
white_horse_king88 (19:43:05)
Form 1,x,y,xy, or 1,x,x^2,x^3. X and y are prime.
Zratonx (19:43:13)
use prime factorization backwards
pika (19:43:18)
x^3 or xy
fubu (19:43:19)
x, y must be primes
MCrawford (19:43:47)

MCrawford (19:44:11)
We can now break the problem into the two cases for the forms of the integers we are looking for.
MCrawford (19:44:28)
snare27 (19:44:39)
4
snare27 (19:44:41)
2, 3, 5, 7
vfiroiu (19:44:45)
4
RC-7th_? (19:44:46)
2,3,5, and 7 could be p, so 4
Mr.Ocax (19:44:46)
2^3, 3^3, 5^3, 7^3
MCrawford (19:45:41)
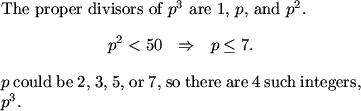
Zyloch_2 (19:45:13)
since 7^2 still < 50
vfiroiu (19:45:33)
2&4, 3&9, 5&25, 7&49
pika (19:45:22)
err, 7 squares less than 50, 4 primes
MCrawford (19:46:15)
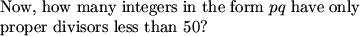
frodo (19:45:49)
The primes are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, and 47.
Zyloch_2 (19:43:36)
15 prime #s under 50
Derek (19:43:42)
list the prime numbers from 1 to 50
vfiroiu (19:43:59)
find the number of primes lass than 50
rachel (19:45:21)
2 primes: 15*14/2=105
Derek (19:46:22)
15 C 2
thinkingmachine (19:46:22)
15 choose 2
rachel (19:46:27)
15x14/2=105
RC-7th_? (19:46:25)
The are 15 primes less than 50, so C(15,2)=105
xirtamax (19:46:28)
15C2
crazygeniuskid (19:46:30)
15C2
MCrawford (19:47:08)
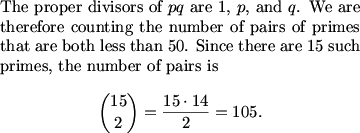
RC-7th_? (19:43:28)
If the number has 3 proper divisors, it has 4 factors. So it must be of the form p*q or p^3, where p and q are prime. Then we look at the primes under 50 for p*q. There are 15 primes, so there are C(15,2) numbers of the form p*q that satisfy the condition. Then we look at p^3, see that p^2 is less than 50, so it could be 2,3,5 or 7. 4+105=109
arkajit (19:45:27)
now we can list primes and see how many we want; there are 15 primes less than 50 and we can choose only two; and they're are 4 primes whose square is less than 50 - so we have 15 C 2 + 4
rachel (19:47:05)
105+4=109
thinkingmachine (19:47:22)
added to 4 gives the answer of 109
smiley_2 (19:47:31)
105+4=109 total.
MCrawford (19:47:55)
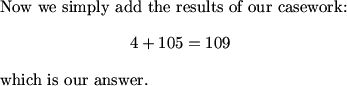
MCrawford (19:48:06)
The keys to this problem were understanding how to count the number of divisors of an integer well enough to break this problem into cases and then knowing how to count within those cases in an organized way.
kky1638 (19:48:02)
that is cool solution
MCrawford (19:48:19)
These are skills that the AoPS Introductory Number Theory and Counting & Probability classes focus on.
thinkingmachine (19:48:19)
can we go over number 14?
MCrawford (19:48:31)
We're going over all the problems in order.
MCrawford (19:48:38)
Now, let's take a look at number 4.
MCrawford (19:48:51)

MCrawford (19:49:07)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-245314190.gif
MCrawford (19:49:15)
What is the first thing we need to do with this problem?
fubu (19:49:16)
n=number of people, n=a^2+5, n=c(c+7)
rachel (19:49:24)
write eq
thinkingmachine (19:49:25)
set up two equations
solafidefarms (19:49:27)
Write it in an equation
MCrawford (19:49:55)
The first thing we need to do is translate the words into math.
rachel (19:49:03)
a(a+7)=b^2+5
Mr.Ocax (19:49:15)
so x(x+7)=y^2+5, and we solve for x using the quadratice formula
pika (19:49:16)
x^2+5=y(y+7)
solafidefarms (19:49:17)
k(k+7)=n^2+5
sponge008 (19:49:19)
x^2+5=y(y+7)
Bassooner (19:49:20)
x^2+5=c^2+7c
snare27 (19:49:31)
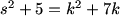
conartist (19:50:08)
y < X < y+7
MCrawford (19:50:34)
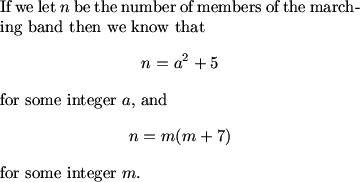
MCrawford (19:51:01)
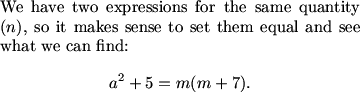
MCrawford (19:51:14)
What's the easier part of this equation to focus on?
fubu (19:50:47)
you can create then a quadratic equation, and use the discriminant to restrict values since the discriminant must be a square of an integer
MCrawford (19:51:38)
I didn't do that, but it might be easier than what I did.
justdudxit (19:51:25)
LHS
rachel (19:51:28)
a^2+5
MCrawford (19:51:48)
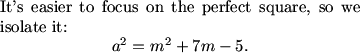
thinkingmachine (19:51:50)
what's LHS?
MCrawford (19:52:00)
left hand side
vfiroiu (19:51:18)
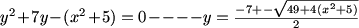
MCrawford (19:52:20)
I haven't followed this solution out, but it may be quicker.
MCrawford (19:52:30)
Now what?
frodo (19:50:19)
Complete the square first?
frodo (19:52:38)
Could you complete the square?
MCrawford (19:52:51)
How exactly?
dbkhoa (19:52:50)
you have to multiple both side by 2
MCrawford (19:53:05)
We could, but it's not necessary.
Bictor717 (19:53:05)
Multiply by 4 to avoid fractions
dbkhoa (19:52:07)
(2a)^2 +69 = (2m+7)^2
MCrawford (19:54:01)
Ah, yes, multiplying by 4 was nice indeed.
MCrawford (19:54:05)
What have we learned here?
frodo (19:54:07)
take the difference of squares next
RC-7th_? (19:54:21)
We can use difference of squares.
dbkhoa (19:54:27)
69=(2m+7-2a)(2m+7+2a)
Zratonx (19:54:28)
two perfect squares with a difference of 69
kostya_4 (19:54:46)
69=3*23
mna851 (19:54:51)
Decompose
mna851 (19:54:53)
69
MCrawford (19:55:09)
Now what?
RC-7th_? (19:55:07)
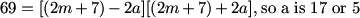
pika (19:55:18)
2m+7-2a=3
2m+7+2a=23
MCrawford (19:55:37)
This gives the 5.
MCrawford (19:55:47)
Where does the 17 come from?
dbkhoa (19:55:14)
but we need the maximum a, so it should be 1*69
MCrawford (19:56:09)
The same equations = 1 and 69 give a = 17.
krustyteklown (19:56:09)
2m+7+21=69
RC-7th_? (19:55:54)
2m+7-2a=1 and 2m+7+2a=69
Yagmoth0000 (19:56:12)
i
Someone (19:56:16)
m=3
justdudxit (19:56:16)
Why can't 69 = 1*69
dbkhoa (19:56:07)
2m+7+2a=69
2m+7-2a=1
pika (19:56:05)
use 1 and 69 instead of 3 and 23
RC-7th_? (19:50:53)
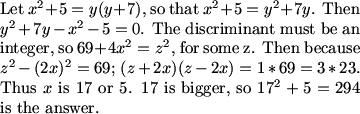
fubu (19:53:56)
i did c^2+7c-(a^2+5)=0, so discriminant is 49+4a^2+20, which is equal to some integer, m, squared, so 4a^2+69=m^2, m^2-4a^2=69, so (m+2a)(m-2a)=69=1*69=2*23, the maximum will use 1 and 69 so m=35, a=17. so the maximum of n = 17^2+5=294
RC-7th_? (19:56:53)
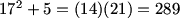
fubu (19:57:03)
m=35, a=17
kky1638 (19:57:05)
add 2 eq.
frodo (19:57:09)
Thus 17^2+5=294
MCrawford (19:57:24)
294 is indeed the answer.
MCrawford (19:57:36)
Probably most students who got the right answer on this problem plugged in numbers until they found the right answer. That just goes to show that grinding out calculations can sometimes help with a problem.
MCrawford (19:57:42)
Soon AoPS plans to offer an Intermediate Number Theory course which will cover, among other things, equations involving integers and divisibility considerations.
MCrawford (19:58:04)
It's fortunately looking like this will take less than 3 hours!
MCrawford (19:58:10)
Let's move to number 5 now.
MCrawford (19:58:20)

MCrawford (19:58:31)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-107057566.gif
Mr.Ocax (19:58:33)
oo.. i personaly enjoyed this one
MCrawford (19:58:48)
What is interesting about this counting problem?
krustyteklown (19:58:41)
first consider only faces, then consider coloring of coins
justinian (19:58:47)
find the possible ways of arranging the color of coints, and the ways of arranging the faces
fubu (19:58:47)
find out how many ways you can arrange the colors first before you find out how many ways to arrnage the face up /face down's
dbkhoa (19:58:57)
just forget the face first
aerlinndan (19:59:03)
Can we consider this problem two separate parts: the colors part and the face-up or face-down part?
MCrawford (19:59:32)
This counting problem involves two independent counting tasks. We need to find the number of possible orders of the 8 coins and also the number of ways each order can be arranged such that coins are never face to face.
MCrawford (19:59:51)
How many possible orders are there for the 8 coins?
RC-7th_? (19:58:48)
First look at the coins as indistingusible, then multiply by C(8,4)=70
frodo (19:58:50)
There are C(8,4) ways to arrange coins regardless of position.
ChrisChang (19:59:01)
we can symbolize this: gold coins are ""a"" and silver are ""b"", so we are mixing up aaaabbbb
Bassooner (19:59:12)
use pascal's triangle to find that the number of possible arrangements of just silver and gold coins, no matter what facing, which is 70.
fubu (19:59:47)
there are 8!/(4!4!)=70 ways to arrange color only
MCrawford (20:00:30)
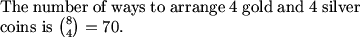
MCrawford (20:00:50)
Now, in how many ways can any one sequence of gold and silver coins be stacked such that no two coins are face to face?
conartist (19:59:09)
9 ways of arranging the faces
thinkingmachine (19:59:21)
number of ways to arrange 8 coins not counting heads up or down is (8 choose 4)
and then the number of ways to arrange heads up and heads down is 9
snare27 (19:59:22)
Isolating the arrangments of the faces of the coins, they can be stacked so that 0 through 8 of the coins face either directions, totaling to nine arrangements regardless of color.
vfiroiu (19:59:31)
face-wise, there are 9 different arrangements-1st coin facing up, 2nd coin up, 3rd.......8th coin up or all coins down
Mr.Ocax (20:00:14)
then there are 9 ways to place them so they aren't face together
Bassooner (20:00:52)
DDDDDDDD
DDDDDDDU
DDDDDDUU
DDDDDUUU
DDDDUUUU
DDDUUUUU
DDUUUUUU
DUUUUUUU
UUUUUUUU
is the different number of facings, so the number of face arrangements is 9
snare27 (20:01:20)
There are 9 ways, because each stack can have the bottom 0 through 8 coins face down
MCrawford (20:01:39)
When stacking the coins from bottom to top, we can never go from a face up coin to a face down coin. Since the coins can never switch back to face down after they are face up, there is at most one switch between face up/down (from down to up). There are two stacks without a switch (all up or all down) and 7 places between coins where a switch could occur. This means there are 9 possible up/down states for the coins.
MCrawford (20:01:51)
Really we could just think of the possible switch points as including the spaces before or after the coins, so there are 8 + 1 = 9 possible switch points.
MCrawford (20:01:55)
What is our final answer?
peter (19:59:09)
9 head-tail combinations, C(8,4) ways to order silver and gold, so 9*C(8,4) = 630
rachel (19:59:24)
8C4 *9 =630
Mr.Ocax (20:00:21)
so 70*9=630
rachel (20:00:43)
8C4 *9=630
chesspro (20:01:01)
We can pick any number from 0 to 8 coins to be facing down, so 70 * 9 = 630.
Bassooner (20:01:10)
9*70=630
RC-7th_? (20:01:22)
9*70=630
frodo (20:01:27)
70*9=630
vfiroiu (20:01:38)
9*70=630 different ways
conartist (20:01:40)
9*70=630 total ways
smiley_2 (20:01:53)
9*70=630
MCrawford (20:02:44)
Geoffrey has a nice way to wrap this up into one problem!
Geoffrey (20:01:59)
hey. if we consider the flip from down to up as |, isn't it just the number of permutations of GGGGSSSS|?
MCrawford (20:03:30)
It is important to analyze the interesting facets of a problem. Once we broke this problem into two and recognized the independence of the two parts, the calculations were not that difficult.
Bictor717 (20:03:12)
9!/(4!4!)=630, neato
sponge008_2 (20:03:12)
Wow, that is really elegant!
justinian (20:03:45)
hmm, that's nice
Sly Si (20:03:47)
Neat!
MCrawford (20:04:00)
This problem is similar to some problems covered in the AoPS Counting & Probability classes.
MCrawford (20:04:15)
Moving on to problem 6.
thinkingmachine (20:04:14)
advertising all the way, eh???
MCrawford (20:04:46)
To be sure, the school and the books fund the entire site and the Math Jams are a way to find students capable of this caliber of problem solving.
miraculouspostmaster (20:04:47)
durn straight
thinkingmachine (20:04:58)
just kidding, i take that back...
MCrawford (20:05:09)
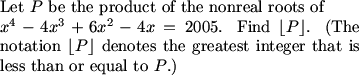
MCrawford (20:05:16)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-39478121.gif
MCrawford (20:05:24)
What is interesting about the given equation?
miraculouspostmaster (20:05:20)
ooh oooh add 1!
chesspro (20:05:23)
Add one and factor.
pika (20:05:30)
Add 1 to make (x-1)^4=2006.
alan (20:05:35)
add 1 and factor into (x-1)^4=2006
corpulus (20:05:37)
it's a binomial expansion
MithsApprentice (20:05:41)
binomial coefficients
conartist (20:05:35)
almost fourth power
WarpedKlown1335 (20:05:35)
It's a binomial expansion.
snare27 (20:05:28)
Noticing the the coefficients look like a row of Pascal's Triangle, add one to each side of the equations. Then factor it into (x-1)^4=2006.
MCrawford (20:07:16)
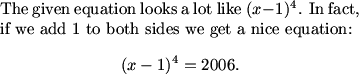
MCrawford (20:07:34)
Now how do we analyze the nonreal roots?
justdudxit (20:06:31)
Its like roots of unity...
pika (20:06:08)
fourth roots of 2006
vfiroiu (20:06:31)
permutations of 1, -1, i and -i
frodo (20:06:56)
Find the four fourth roots of 2006.
MCrawford (20:08:28)
Do we need all four?
joml88 (20:07:29)
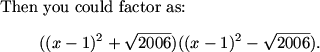
RC-7th_? (20:07:31)
Take the fourth root of both sides to get x-1=2006^(1/4). However, we're not only looking at real roots, so x-1 equals 2006^(1/4) or 2006^(1/4)*i or -2006^(1/4) or -2006^(1/4)*i. But we only need to look at the roots with i in then.
conartist (20:07:48)
nonreal comes in conjugates
MCrawford (20:08:57)

WarpedKlown1335 (20:07:52)
The nonreal roots will be the roots of the equation (x-1)^2 = -sqrt(2006)
chesspro (20:07:54)
Square root it, toss out the positive root, expand, and you have product of roots.
dbkhoa (20:08:09)
(x-1)^2=+/-sqrt(2006)
pika (20:06:41)
x-1=+-fourthroot(2006);+-i*fourthroot(2006)
mna851 (20:07:16)
Subtract the 2006 and do the difference of two squares. Factoring the (x-1)^2+2006=0 Will give you nonreal roots.
MCrawford (20:10:04)
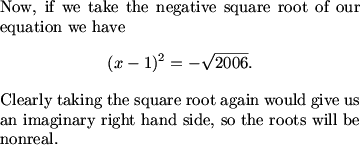
MCrawford (20:10:23)
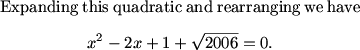
pika (20:07:46)
floor (1+sqrt2006)
dbkhoa (20:10:16)
for the non-real roots, it'll be the roots of x^2 -2x+1+sqrt(2006)=0
MCrawford (20:11:08)
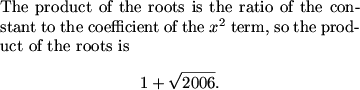
justdudxit (20:10:52)
P = 1+rad(2006) => 45
fubu (20:09:36)
ohh..i did ((x-1)^2-sqrt2006)((x-1)^2+sqrt2006)=0, so we know (x-1)^2+2006 =0 will give non real roots so that becomes x^2-2x+1+sqrt2006=0, so the products will be 1+sqrt2006, since int(sqrt2006) is 44, then the answer is 45
mna851 (20:10:46)
Viete's theorem c/a
MCrawford (20:11:54)

fubu (20:11:31)
floor(sqrt2006)is 44 so floor (1+sqrt2006) is 45
pika (20:11:32)
floor that is 45
MCrawford (20:12:15)
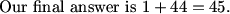
rachel (20:08:47)
I found the product of all roots and divided by the product of real roots
corpulus (20:08:56)
you can divide the product of the roots by the two real roots
MCrawford (20:12:47)
That's certainly an option.
MCrawford (20:12:52)
The key to working this problem efficiently was noticing that we had a nice way of manipulating the algebra without trying to hunt down the actual roots to the fourth degree polynomial. It pays to be aware of common binomial coefficients and how to use them.
MCrawford (20:13:03)
It was also important to recognize that taking the square root immediately separately the polynomial into two quadratics with real and unreal roots respectively. This reduced our problem to a problem of two variables that was far more tractable.
MCrawford (20:13:12)
This problem is similar to some that we work in the Intermediate Algebra class.
MCrawford (20:13:34)
Problem 7:
MCrawford (20:13:38)
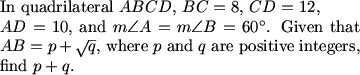
MCrawford (20:13:41)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-29759086.gif
MCrawford (20:13:53)
Where should we start with this one?
sponge008_4 (20:13:50)
We need a diagram...
Someone (20:13:51)
draw diagram
RC-7th_? (20:13:53)
Draw a picture!
alan (20:13:56)
draw picture!
conartist (20:13:57)
diagram
mna851 (20:13:59)
Draw a picture of course
MCrawford (20:14:21)
It's always good to start with a nice, clean, easy to view diagram -- EASY TO VIEW. The difference between seeing through a problem such as this one is often the difference between being able to read information into your own diagram.
MCrawford (20:14:24)

MCrawford (20:14:40)
What is interesting about the diagram?
pika (20:14:25)
use the 60degrees!
sponge008_4 (20:14:51)
It's almost isoceles...
fubu (20:14:53)
the 60 degree angles.
kops723 (20:14:58)
there are 2 60 degrees
dts (20:14:59)
60 degree angles... begging for 30-60-90.
MCrawford (20:15:38)
The twin 60 degree angles look interesting.
arkajit (20:14:03)
break it into an isosceles trapezoid and triangle
krustyteklown (20:14:01)
extend DC and AD to form an equilatrel triangle
MCrawford (20:16:13)
Both good approaches. I took the first.
MCrawford (20:16:18)
If we draw a segment from C to AD parallel with AB we have an isosceles trapezoid:
MCrawford (20:16:26)

MCrawford (20:16:29)
Here I went ahead and filled in angle information. This is an important step in working with any diagram (and another reason to make your diagram big enough to work with).
snare27 (20:13:54)
Draw altitudes from points C and D, making two 30-60-90 right triangles
Mr.Ocax (20:14:08)
and you will have 30-60-90 triangles
pika (20:14:37)
create 30-60-90 triangles!
conartist (20:14:37)
drop altitudes to AB from d and C
conartist (20:14:57)
you can construct many right triangles
ChrisChang (20:15:02)
we can make 30-60-90 triiangles
sponge008_4 (20:15:15)
Oh, we have an is. trap, and a tri
MCrawford (20:17:48)
We can now drop altitudes from C and E to AB giving nice 30-60-90 right triangles with which to work:
MCrawford (20:17:51)

MCrawford (20:18:10)
We see that the smaller legs are half each hypotenuse and are of length 4.
chesspro (20:16:50)
Law of cosines.
arkajit (20:17:14)
and use law of cosines on the triangle to find EC
Someone (20:15:43)
law of cosines any good here?
arkajit (20:18:19)
and EC will equal the missing piece we need to find AB
MCrawford (20:19:33)
We see that AB is 8 more than EC due to the nice rectangle that sprang up in our diagram.
MCrawford (20:19:38)
We can see that angle CED is 60 degrees giving us the opportunity to apply the law of cosines to the problem.
vfiroiu (20:19:17)
what if u dont know trig like me?.....
guangweicao (20:18:49)
instead of laws of cosines, draw a perpendicular from D to AB
guangweicao (20:18:56)
its much easier and does not require trig
MrsB (20:19:57)
If you darw 30-60 90 to D instead of e it works out beautifully
snare27 (20:19:45)
I dropped the altitudes directly from C and D, and then made a third right trianle by extending a line from C perpendicular to the existing right triangles. This triangle had a hypotenuse of 12 and on leg equal to the difference if thte legs of the two 30-60-90 triangles.
MCrawford (20:20:42)
I tend to seek out symmetries with Geometry problems, so it is likely I did not find the solution with the lowest level of machinery.
lotrfan (20:19:26)
4+x^2-2x=144, x=EC
MCrawford (20:20:53)
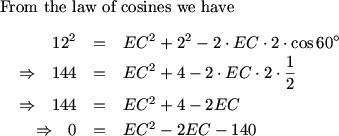
pika (20:20:40)
Yes, so length of AB is 9+sqrt(141)
MCrawford (20:21:38)
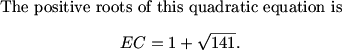
fubu (20:18:10)
using the equilateral triangle method, we label AB=x, label the point where the extensions of AD and BC meet as E, so ED=x-10 and CE=x-8. since <E=60 degrees, we can use the law of cosines. so 144=(x-8)^2+(x-10)^2-2(x-8)(x-10)*1/2, after algebra we find that x=9+sqrt141 so the answer is 150
peter (20:20:29)
I dropped perpendiculars from D and C to AB at points E and F, then from C to DE at G, so DE is 5rt3 CF is 4rt3, so DG is rt3, so CG is rt141, because DEFC is rectangle, AB is 9 + rt141, so answer is 150
Mr.Ocax (20:21:33)
so 141+9=150
MCrawford (20:22:35)
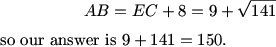
MCrawford (20:23:27)
The key to solving this problem was recognizing the interesting feature of the initial diagram, namely, the twin 60 degrees angles that allowed us to draw a nice isosceles trapezoid into our diagram. From there, the angle work was nice and we simply needed to apply the law of cosines to get the length of EC.
MCrawford (20:23:37)
Recognizing the interesting feature of a diagram is taught in all of the AoPS Geometry classes and the law of cosines is discussed in length in the AoPS Intermediate Trigonometry/Complex Numbers class.
conartist (20:19:44)
another way is if you drop the altitudes from D and C onto AB, you would have the right triangle containing DC to have side of rad3 and a hyp of 12. and apply pythagorean thereom.
ginasboys (20:21:25)
Um. from the way I did. I dropped an atltitude from D to AB (at F), and then another altitude from C to DF. Then DEC is a right triangle. So no LoS is used and it's purely elementary Pathygorem thms...
MrsB (20:21:27)
Get d's Perpendicular is 5rt3 and C's perpendicular is 4rt3, so side on top triangle is 1rt3
Sly Si (20:21:40)
I solved it using the equilateral triangle method--the existence of a 30-60-90 triangle never even occurred to me!
krustyteklown (20:22:49)
did same as fubu
vfiroiu (20:16:16)
i had AD and BC connecting at the bottom to get an equilateral triangle
dts (20:17:56)
Drop perpendiculars DF and CG to AB, then drop a perpendicular from C onto DF. The answer is simple from here.
kky1638 (20:23:28)
so we can do this without trig.
MCrawford (20:24:19)
Indeed, my solution was not the simplest.
MCrawford (20:24:33)
Dave Patrick is now going to take over for a couple of problems.
DPatrick (20:24:46)
Hi
DPatrick (20:24:48)
Problem 8:
DPatrick (20:24:51)

DPatrick (20:24:56)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-53367102.gif
RC-7th_? (20:25:03)
Replace 2^(111x) with y
thinkingmachine (20:25:07)
let b = 2^(111x)
peter (20:25:08)
substitute y for 2^111x
Mr.Ocax (20:25:09)
could we do y=2^111x?
lotrfan (20:25:18)
Definitely suggests a substitution.
Myself (20:25:29)
it seems as if substituting 2^(111x)=y would work well here
DPatrick (20:25:42)
The most obviously interesting aspect of the given equation is that the exponents involve 111x, 222x, and 333x. This gives a rather ugly equation.
DPatrick (20:25:54)
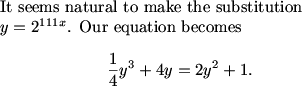
DPatrick (20:26:05)
Now, what exactly do we want out of this equation?
thinkingmachine (20:26:24)
find the products of the roots
frodo (20:26:26)
The product of y's roots.
dts (20:26:26)
The product of the solutions for y, since that gives us the sum of the solutions for x.
dbkhoa (20:26:52)
we want y1*y2*y3
DPatrick (20:27:16)
It is easy to jump to thinking that we now want to find the sum of the roots of our new equation, but there is something wrong with this idea.
DPatrick (20:27:23)
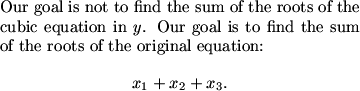
DPatrick (20:27:39)
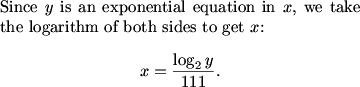
DPatrick (20:27:51)
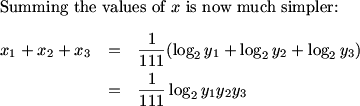
dbkhoa (20:27:38)
because 111(x1+x2+x3)= log(2)(y1)+log(2)(y2)+log(2)(y3)
ginasboys (20:27:19)
Since we make the substitution 2^111x = y, or log2 y ./ 111 =x. Consider 3 solutions x_1, x_2, and x_3. We are interested in log2 (y_1 *y_2 * y_3). Or the product of roots.
DPatrick (20:28:24)
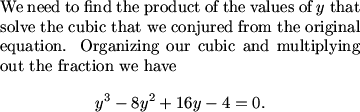
DPatrick (20:29:04)
What is the product of the roots?
frodo (20:28:27)
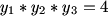
rachel (20:28:49)
product of roots =4
Someone (20:29:09)
product=4
justdudxit (20:29:13)
4
pika (20:29:14)
4
sleepsta (20:29:15)
4
smiley_2 (20:29:16)
4
DPatrick (20:29:29)
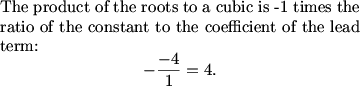
DPatrick (20:29:36)
What is our final answer?
ginasboys (20:29:43)
2/111
frodo (20:29:48)
2/111 2+111=113
kops723 (20:29:50)
2/111
ginasboys (20:29:50)
2/111 => 113
justdudxit (20:29:51)
2/111 => 113
dbkhoa (20:29:52)
2/111
flierdeke (20:29:55)
113
DPatrick (20:30:08)
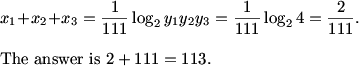
DPatrick (20:30:22)
This problem is a great example of how identifying the ugly aspect of an equation can lead us down the best solution path. Here we employed a nice substitution that gave us a much cleaner equation to work with. However, we still had to recognize the relationship between the variables as we applied the exponential function in our substitution. Find the sum of the roots of the original equation meant using the inverse of the exponential function (logarithms) to relate the original problem to the new equation.
DPatrick (20:30:33)
These kinds of substitutions and functional considerations are covered in the AoPS Intermediate Algebra class.
DPatrick (20:30:44)
Problem 9:
DPatrick (20:30:47)
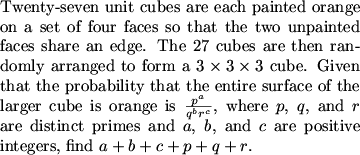
DPatrick (20:30:56)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-212577278.gif
DPatrick (20:31:10)
What about this problem gives us a reasonable starting point?
rachel (20:31:13)
3 cases, 1-3 faces showing
vfiroiu (20:31:21)
3 cases: cube on surface, on edge, or on corner
Myself (20:31:27)
8 corners, 12 edges, 6 faces 1 center cube
DPatrick (20:31:48)
The larger cube is made up of 1 cube in the very center, 6 in the centers of each face, 12 in the middles of edges, and 8 at the corners of the large cube.
DPatrick (20:32:02)
Our classification of the way the cubes are arranged helps us because each of the smaller cubes are the same and we now recognize that instead of viewing the problem as 27 different problems, we can now view the problem as 3 problems (we toss out the cube in the very center because its painting orientation is irrelevant).
DPatrick (20:32:18)
Now, what is the probability that a cube in the center of a face of the larger cube shows only orange?
ChrisChang (20:32:19)
can we ignore the center cube?
DPatrick (20:32:52)
Yes, because it's orientation doesn't affect the outside of the big cube at all.
peter (20:32:33)
4/6
rachel (20:32:36)
2/3
kops723 (20:32:36)
4/6=>2/3
mna851 (20:32:38)
2/3
Mr.Ocax (20:32:41)
2/3?
Geoffrey (20:32:47)
4 good / 6 possible = 2/3.
flierdeke (20:32:50)
4/6 = 2/3
frodo (20:32:52)
2/3
pika (20:32:56)
4/6 chance
DPatrick (20:33:11)
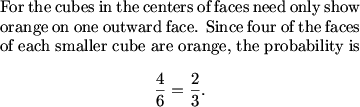
DPatrick (20:33:30)
Now, what can we do to help us determine the probability that a smaller cube on an edge of the larger cube shows only orange?
DPatrick (20:33:53)
A model might help us here:
DPatrick (20:33:59)

DPatrick (20:34:10)
Thinking about the cubes as dice might help us. This helps us model the fact that the unpainted faces are adjacent which is essential to getting the right answer.
We will let the unpainted faces be the ones labeled 1 and 2.
DPatrick (20:34:32)
Now, how many orientations are there for the cube (in terms of the numbers)?
kops723 (20:34:45)
24
ChrisChang (20:34:54)
24
justdudxit (20:35:02)
24
MPS-vras (20:35:06)
24
DPatrick (20:35:23)
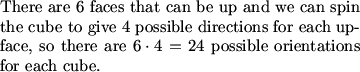
DPatrick (20:35:34)
For how many of those orientations will both (adjacent) exposed faces of the cube be orange?
DPatrick (20:37:08)
There are several ways we could perform this count, but complementary counting works for us. We can count the number of ways in which at least one unpainted face is exposed:
DPatrick (20:37:13)

DPatrick (20:37:20)
Suppose the two exposed faces are where the 1 and 2 are in this picture.
There are 2 orientations in which both unpainted faces are exposed.
DPatrick (20:38:02)
How many orientations expose one painted face and one unpainted face?
frodo (20:37:58)
12 with just one.
pika (20:38:31)
12
DPatrick (20:38:45)
Right, there are 2 places one unpainted face could be exposed and 2 unpainted faces that could occupy those places. For each of those circumstances there are 3 orientations such that the other exposed face is painted (discounting the fourth orientation in which both unpainted faces are exposed).
DPatrick (20:39:03)
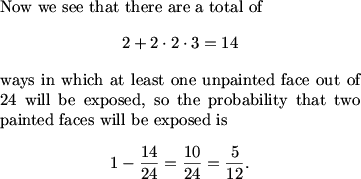
DPatrick (20:39:18)
There are other ways we could have come up with this probability.
DPatrick (20:39:32)
We could have directly counted the number of orientations with both painted faces exposed.
DPatrick (20:39:37)
Or, we could have focused on edges, as such:
thinkingmachine (20:35:55)
it's just the number of edges not touching an unpainted face... since there are 7 such edges, we have 12 - 7 for a total of 5 such orientations
DPatrick (20:40:14)
Now how can we determine the probability that a small cube at the corner of the large cube will have only orange faces exposed?
Someone (20:40:36)
it must have 3 faces exposed
Mr.Ocax (20:40:59)
only 2 ways to place it
Sly Si (20:41:01)
The vertex that serves as the vertex of the large cube must border three orange faces. There are two such vertices, so the probability is 2/8=1/4.
DPatrick (20:41:35)
Right -- the positioning of a corner cube is determine by the vertex that forms the corner of the big cube.
DPatrick (20:41:55)
Only 2 of the 8 vertices of the small cube lie where 3 orange faces meet.
DPatrick (20:42:07)
So the probability is 2/8 = 1/4.
DPatrick (20:42:17)
Now, how do we determine the final answer?
white_horse_king88 (20:42:55)
Raise each to the power of the number of cubes there are with the certain number of exposed faces.
ginasboys (20:43:00)
There are 8 corners, 12 edges, and 6 centers. Thus (1/4)^8 * (5/12)^12 * (2/3)^6 is our desired probability.
dbkhoa (20:43:02)
power each of the posibilities to the number of small cubes
RC-7th_? (20:42:42)
So we have (5^12)/(2^34*3^18), so we have 5+12+2+34+3+18=74
rachel (20:43:09)
(2/3)^6*(5/12)^12*(1/4)^8, cancel 2s, add components to get 74
lotrfan (20:43:10)
cancel stuff out and split up according to the form given in the problem after multiplying the probabilities raised to the power representing the number of times that type of cube occurs.
DPatrick (20:43:28)
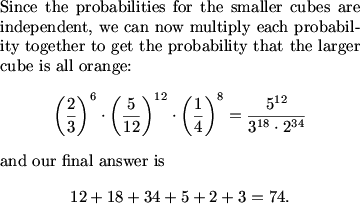
DPatrick (20:43:46)
This problem tested our ability to organize independent probabilities into cases and also find a way to model the orientations of a cube with the specific conditions that the two unpainted faces are adjacent. If you organize your work well and follow a good model from beginning to end, solutions such as this are very attainable.
DPatrick (20:44:14)
OK, I'm going to turn things back over to Mathew Crawford, who will take you the rest of the way.
MCrawford (20:44:26)
Let's take a look at problem 10.
MCrawford (20:44:35)

MCrawford (20:44:43)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-215713278.gif
MCrawford (20:44:53)
Where can we start with this problem?
Bassooner_2 (20:44:51)
Dra a diagram
frodo (20:44:52)
Draw a coordinate plane.
MCrawford (20:45:07)
We don't really need a diagram for this one.
kops723 (20:45:04)
midpoint of BC
snare27 (20:45:25)
Find the equation the line with slope -5 that intersects the midpoint of BC
mna851 (20:45:26)
We can find the equation of the median
MCrawford (20:45:44)
We can begin by determining the line on which the median to BC lies.
Mr.Ocax (20:45:35)
we know that the line equation is y=-5+107
MCrawford (20:46:10)
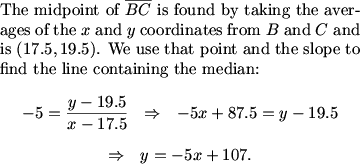
origamimasterjared (20:46:10)
And the equation of the median (y=-5x+107)
ginasboys (20:45:47)
Do we want to translate the triangle? (like we did in class)
MCrawford (20:46:33)
We could do that, but it's not necessary.
MCrawford (20:46:44)
Where can we go from here?
Zyloch_2 (20:45:15)
u can find area with determinants
joml88 (20:45:45)
Express area in terms of the determinant of a matrix and use the slope formula to set up a system of equations.
justdudxit (20:45:57)
Use a matrix method to equate p and q with a number
kops723 (20:46:47)
from here there will be 2 answers
MCrawford (20:47:17)
We are trying to find the values of x such that the triangle with coordinates (12, 19), (23, 20), and (x, -5x + 107) has area 70.
We could at this point resort to hunting down the nasty form of the distance from (x, -5x + 107) to the line containing B and C and using that as the height of the triangle, but there is a method for finding the areas of triangles that saves us a lot of trouble.
Sly Si (20:47:04)
Pick's Theorem give the area as a linear function of p and q!
MCrawford (20:47:32)
Pick's assumes lattice points.
lotrfan (20:47:32)
cross products give areas, and this method can be generalized using determinants.
mna851 (20:47:46)
Or Heron's theorem but that might get extremely messy.
MCrawford (20:48:05)
The area of a triangle is half of the absolute value of the determinant of the 3 x 3 matrix whose first column contains the values of the x-coordinates of the triangle, second column contains the values of the y-coordinates, and third column contains only 1's.
dts (20:45:42)
Use the formula: |determinant(p,q,1;12,19,1;23,20,1)|=area of triangle=1.
MCrawford (20:48:20)
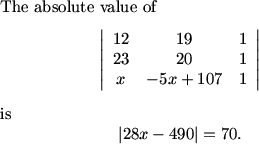
Bassooner_2 (20:48:16)
but if the answer asks us to add p and q and come up with an integers, aren't p and q both lattice points?
MCrawford (20:48:53)
Because the sum of two numbers is an integer does not mean they are both integers.
MCrawford (20:49:02)
However...
lotrfan (20:48:58)
don't we need to take one half of the determinant?
MCrawford (20:50:00)
Yes, sorry, forgot that.
MCrawford (20:50:14)
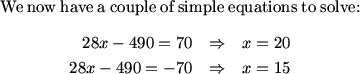
MCrawford (20:50:29)
What is our final answer?
fubu (20:47:47)
i used the matrix equation for using coordinates to find the area and got 11q-p=337. Then I used the midpoint of BC(35/2, 39/2) and pq to find a relationship for the -5 slope. i got 5p+q=107. so then q=32 and p=15. answer=47
Mr.Ocax (20:50:29)
we want 15
frodo (20:50:40)
107-15*4=47
fubu (20:50:50)
find the x that will maximize!
justdudxit (20:50:59)
20 is out of range
MCrawford (20:51:17)
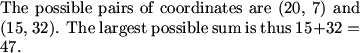
MCrawford (20:51:20)
We could also have noted that we needed only the smaller value of x as the sum of x and -5x + 107 is -4x + 107 which is a decreasing function. This means we're looking for the smaller value of x.
Bassooner_2 (20:50:33)
What was your however?
MCrawford (20:51:42)
I was thinking about whether we could imply from y = -5x + 107 and x + y = n that x and y are integers.
MCrawford (20:51:46)
Can we?
justdudxit (20:52:12)
no
Myself (20:52:18)
no. x = 1.5
pilot (20:52:19)
No
pika (20:52:30)
-4x+107=n
vfiroiu (20:49:58)
How would u solve this problem without a matrix?
joml88 (20:51:29)
Are there any 'nice' solutions without a matrix.?..it seems a little unlike them to require knowledge of a matrix to solve an AIME problem...
Geoffrey (20:53:05)
can we multiply all coordinates by four and use pick's? :-)
MCrawford (20:53:30)
Nice work Geoffrey!
MCrawford (20:53:37)
That's one possibility.
Mr.Ocax (20:53:47)
why multiply by 4?
MCrawford (20:54:03)
So that all the coordinates are necessarily integers.
justdudxit (20:53:56)
There's a sleight-of-hand trick you can use without a matrix. Hang on.
Bictor717 (20:47:38)
find the length of the height and use distance from point to line
MCrawford (20:54:34)
That's going to be a grind, but certainly possible.
Geoffrey (20:54:29)
because y+5x is integer, and x+y is integer, 4x and thus 4y are integers
origamimasterjared (20:54:16)
Wouldn't Pick's take too long?
MCrawford (20:55:06)
That depends on what kinds of calculations you are good at performing quickly.
origamimasterjared (20:54:49)
And it would be dangerous, because you could easily miscount.
Bassooner_2 (20:54:56)
we have 3 hours
kops723 (20:54:43)
you can use the shoelace theorem (don't know its oficialy name) where you line up all the coordinates vertically and then cross multiply by kind of drawing in a shoelace
Myself (20:55:17)
how do we find internal points?
MCrawford (20:55:33)
Inequalities.
kops723 (20:55:20)
what exactly is picks ive never heard of it
MCrawford (20:55:51)
We don't have time for a full discussion. Best to ask further on the message board.
DPopov (20:55:40)
I would recommend the shoelace
DPopov (20:55:44)
it worked nicely
DPopov (20:55:54)
since you have y in terms of x
Zratonx (20:56:00)
that is based on matrix...the ""the shoelace theorem""
MCrawford (20:56:17)
Let's move on to problem 11.
Mr.Ocax (20:56:14)
someone please post shoelace on the board too!!
MCrawford (20:56:31)
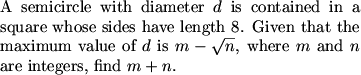
MCrawford (20:56:41)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-87568638.gif
MCrawford (20:56:47)
Without even jumping to a diagram, what can say about the relationship between the semicircle and the square?
mna851 (20:57:06)
They are tangent
pilot (20:57:08)
Tangent
Bictor717 (20:57:08)
semicircle is inscribed
MCrawford (20:57:26)
Actually, that's not trivial to prove.
MCrawford (20:57:41)
Many students got away with making this assumption however.
kops723 (20:57:46)
but it has to be otherwise it could be enlarged
MCrawford (20:58:12)
That's not yet clear and I've seen geometry problems where such an intuitive idea was false.
vfiroiu (20:58:07)
y prove it if u got 3 hours?
MCrawford (20:58:31)
You don't need to on the AIME of course, but that's why I personally thought this problem was a mistake.
MCrawford (20:58:47)
We know that the two endpoints of the semicircle will lie on sides of the square. If not, we could clearly expand the semicircle until they did hit sides.
MCrawford (20:58:49)

MCrawford (20:59:14)
Many of you want to jump to the conclusion that the diagram is symmetric and that the semicircle touches the square on all four sides (including the endpoints).
MCrawford (20:59:33)
The fact is that the largest semicircle does hit the square on all four sides, but it's not exactly obvious as to why this is true. I don't think the AIME committee intended for this step to be so obvious and for this reason this probably shouldn't have been a number 11.
MCrawford (20:59:41)
What can we do that would help us examine the orientation of the semicircle?
kops723 (21:00:02)
make it a full circle
MCrawford (21:00:33)
That might help you notice what's coming next.
vfiroiu (21:00:24)
bottom left triangle isosceles and right
MCrawford (21:00:46)
We don't yet know it's isosceles.
vfiroiu (21:00:31)
hypotenuse=diameter
frodo (21:00:49)
The median of the right triangle equal the radius of the circle.
MCrawford (21:01:15)
It makes sense to identify the center of the semicircle (the center of the full circle). This will allow us to begin making comparisons to the radius:
MCrawford (21:01:20)

MCrawford (21:01:27)

MCrawford (21:01:34)
The median from D in right triangle EFD must be half the hypotenuse and is therefore equal to r.
Bictor717 (21:00:19)
draw the radii to the sides of the square
MCrawford (21:01:48)
But we don't yet know that both radii will touch the square!
kostya_4 (21:01:37)
isn't the circle symmetrycal along the bottomleft to top right side...
MCrawford (21:02:14)
That's what we're trying to determine. Nobody has given a reason yet why this is true.
MCrawford (21:02:45)
Now, how can we compare the radius to the side of the square?
rachel (21:03:16)
r+rrt2/2=8
MCrawford (21:03:40)
Still based on assumptions... and nobody has given a reason for those assumptions.
DPopov (21:03:52)
What do we need to prove?
MCrawford (21:04:14)
That the semicircle is inscribed.
MCrawford (21:04:27)
There are many maximal area problems in which the figure cannot be inscribed.
MCrawford (21:05:10)

Someone (21:05:19)
Why not prove that the four points where the circle ""touches"" the square are cyclic?
MCrawford (21:05:43)
Because we haven't proved that the semicircle touches the square at four points.
MCrawford (21:05:49)
Those of you planning taking the USAMO -- beware!
MCrawford (21:06:12)
If you make these kinds of assumptions you'll find 0's on problems you would swear you got a 7 on.
beta (21:05:59)
the semicircle must touch at least 3 sides, or we could expand it
MCrawford (21:06:21)
That is true.
kops723 (21:05:49)
sin(X) = ON/r
MCrawford (21:06:44)
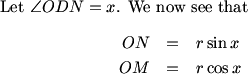
MCrawford (21:07:06)
How does this help us?
Sly Si (21:06:59)
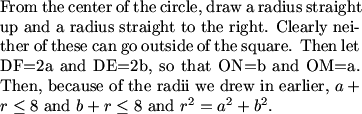
MCrawford (21:07:31)

MCrawford (21:07:42)
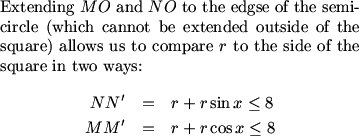
vfiroiu (21:07:58)
so this problem isn't ""proveable"" without trig?
MCrawford (21:08:33)
Myself has an idea that I'll drop in later that doesn't involve trig.
rachel (21:08:10)
MNOD is a square, so x=45
MCrawford (21:08:58)
We don't know that yet. It's only a rectangle by our assumptions.
dts (21:08:41)
Equality must hold for one of those, doesn't it?
MCrawford (21:09:14)
This we know!
MCrawford (21:09:18)
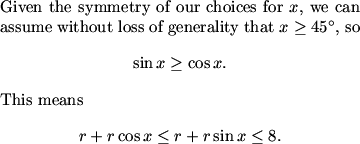
MCrawford (21:09:34)
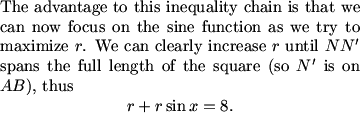
dts (21:09:21)
That is, it holds for the larger one.
dts (21:09:27)
It holds for both iff x=45.
MCrawford (21:10:03)
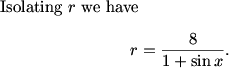
MCrawford (21:10:27)
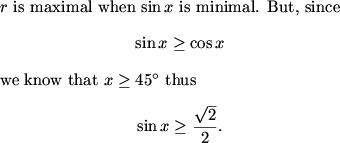
MCrawford (21:10:39)
We have now finally proved what many students got away with assuming -- namely that the figure is symmetric.
MCrawford (21:10:43)
What is our final answer?
DPopov (21:11:14)
DPopov (21:11:00)
544
vfiroiu (21:11:08)
544
pika (21:11:25)
8/(1+1/sqrt2))=x
8/((sqrt2+1)/sqrt2)=x
MCrawford (21:11:35)
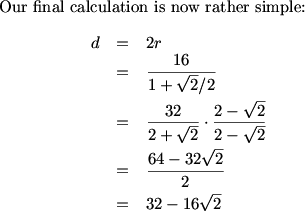
pika (21:11:32)
544
MCrawford (21:11:43)
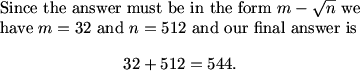
Sly Si (21:11:47)
Don't forget (as I did) that we're not actually looking for r.
MCrawford (21:12:13)
Myself has non-trig proof for the inscribing of the semicircle.
Myself (21:03:37)
AB is tangent to the circle. Let the contact point be D and the center of the circle be O. Then OD is perpendicular to AB because AB is tangent to the circle
Myself (21:06:15)
Let E vary on AD, but let DF = DE. When E is at D, the semicircle is smaller than the square. When E is at A, the semicircle is outside the square. At some point, the semicircle must go from inside to outside; this is the tangent point
MCrawford (21:13:05)
If you can think up this kind of argument, it's rigorous.
MCrawford (21:13:08)
Just be wary of assumptions without reasoning on the USAMO.
MCrawford (21:13:40)
Last year many students thought they got number 3 and got a 0 or a small number for that problem due to false or unproven assumptions.
vfiroiu (21:13:31)
this was alot easier than some of the previous ones
MCrawford (21:14:07)
Yes, but mostly because the intuitive fact that we proved was obvious. That's rare for a USAMO problem.
MCrawford (21:14:17)
On to problem 12.
MCrawford (21:14:26)
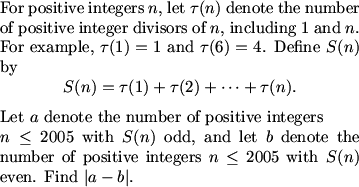
MCrawford (21:14:37)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-12794638.gif
MCrawford (21:14:43)
What do we know that is going to help us with this problem?
frodo (21:14:43)
There is an odd number of factors in squares.
peter (21:14:45)
only perfect squares have odd number of divisors
MCrawford (21:14:54)
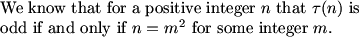
Mr.Ocax (21:14:51)
you know that s changes at perfect squares
fubu (21:14:54)
we know that since the number of factors of a square of a prime is odd, that is when the odd /even pattern changes
Myself (21:14:57)
we need to figure out when S(n) switches parity
MCrawford (21:15:07)
If this fact is new to you, I would suggest trying to prove it on your own. We cover two proofs of this in the AoPS Introduction to Number Theory class.
MCrawford (21:15:26)

Sly Si (21:15:19)
Thus, if you take the sequence S(1), S(2)... it switches parity at perfect squares.
kops723 (21:15:22)
we also know that the difference between two consecutive perfect squares is an odd number
MCrawford (21:15:43)
It we did not see this already, we discover that the parity (modulo 2 residue) of S(n) depends only on the number of perfect squares from 1 to n inclusive.
kops723 (21:15:39)
the difference between the next 2 consecutive squares is the next odd number
MCrawford (21:15:58)
We can now count the number of S(n) that are both even and odd by groups:
S(1) through S(3) are odd.
S(4) through S(8) are even.
S(9) through S(15) are odd.
S(16) through S(24) are even.
S(25) through S(35) are odd.
etc.
rachel (21:15:54)
5+9+...
Myself (21:15:55)
Notice that (n+1)^2 - (n^2) = n + n+1
Geoffrey (21:16:03)
we've got a sequence of 3 odd, 5 even, 7 odd, etc.
MCrawford (21:16:20)
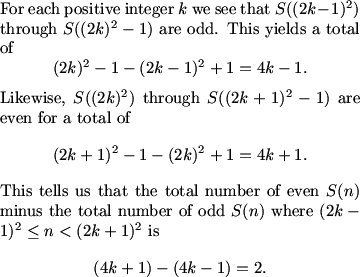
MCrawford (21:16:54)
What is the best way to break up these counts overall?
frodo (21:15:08)
44^2<2005<45^2
kops723 (21:17:23)
for every 2 switches of parity, the positive difference increases by 2 in favor of evenness
MCrawford (21:17:38)
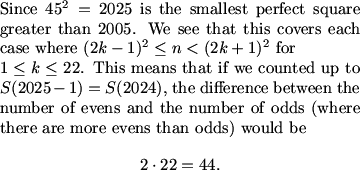
MCrawford (21:17:47)
How do we adjust for our final answer?
Geoffrey (21:17:47)
find out what floor(sqrt(2005)) is, and start with 2 * that, and then take care of everything from (that)^2 up to 2005.
MCrawford (21:18:07)
I went down from 2025, but either is fine.
Mr.Ocax (21:18:05)
you subtract 45^2-2005
MCrawford (21:18:16)
Close.
conartist (21:18:25)
add 1?
Mr.Ocax (21:18:34)
ack!!! my mistake!!!!nooooo
Geoffrey (21:18:52)
2024 -> 44, so 1908+x -> x. 2005 -> 25.
MCrawford (21:19:17)
MCrawford (21:19:39)
There was no one exceedingly difficult step to this problem. However, there were a lot of little things that made it easier. First and foremost, recognizing that there was no need to count the divisors of any integers made the problem approachable. From there, expressing everything in modulo 2 make calculations much easier. The rest of the problem involved reasoning that, if kept organized, was not all that difficult.
MCrawford (21:20:03)
I personally liked the next problem:
MCrawford (21:20:08)

MCrawford (21:20:14)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-151992927.gif
MCrawford (21:20:21)
How might we attack such a problem?
Mr.Ocax (21:20:29)
the no right angle turns makes it much more difficult
dts (21:20:30)
Grind it out!
vfiroiu (21:20:35)
3 possible 1st steps?
alan (21:20:35)
brute force
Blaise (21:20:36)
Draw a diagram.
kops723 (21:20:42)
my coach had a good way--split up the total number of ways into an ordered triple, number of ways coming from below, from left, and from diagonal
MCrawford (21:21:03)
Numerous possible counting methods come to mind when thinking about this problem, though there doesn't seem to be any nice combinatoric approach.
MCrawford (21:21:08)
Sometimes simpler problems can help us get a grip on how we might solve the problem at hand. Sometimes we notice patterns or the essence of the problem.
conartist (21:21:09)
draw a tree, a very big tree [img id=em-3]
MCrawford (21:21:20)
There is only 1 way to get to (1, 1) without a right angle is to go straight there.
MCrawford (21:21:27)
There are 3 ways to go from (0, 0) to (2, 2). We can go through (1, 1), (1, 0), or (0, 1) with one set path from each of those points.
MCrawford (21:21:35)
The number of ways to get to (3, 3) and then (4, 4) looks like it's going to get difficult to count in a simple way rather quickly.
gibsnson (21:21:20)
define it recursively!
MCrawford (21:21:50)
That's what we'll do essentially.
Geoffrey (21:22:08)
it's hard to recurse, because sometimes you come in from a straight line, and you can't turn
MCrawford (21:22:26)
We'll get around that fact.
MCrawford (21:22:32)
We'll have to dig a little deeper into how this counting sequence is defined.
MCrawford (21:22:36)
Perhaps a picture would help:
MCrawford (21:22:39)

MCrawford (21:22:52)
The lower left hand corner is the origin and the upper right hand corner is (5, 5). Here we see the numbers of ways to get to each (1, 0), (1, 1), and (0, 1).
MCrawford (21:23:16)
Let us continue to draw upward paths in pink, diagonal paths in green, and horizontal paths in yellow, but we'll only draw the paths that take us to (2, 2) through some route.
MCrawford (21:23:35)

MCrawford (21:23:44)
It would have been nice if we could have done some simple block-walking labeling here, but the problem is that not all paths that lead from home to each point get counted.
MCrawford (21:24:03)
Given that the algorithm from where we can move each time is defined according to the last move, it makes sense to break the counts down into groups according to which direction the last path was walked:
MCrawford (21:24:10)

MCrawford (21:24:29)
Here the first number in each triplet describes the number of paths such that the last move was horizontal. The second number describes the number of paths such that the last move was diagonal. The third number describes the number of paths such that the last move was vertical.
kops723 (21:24:23)
thats what my coach did!
MCrawford (21:24:44)
According to the given algorithm, each first triplet entry will be the sum of the first two entries from the point immediately to the left. The second triplet entry will be the sum of all three entries from the point to the lower left. The third triplet entry will be the sum of the last two entries from the point immediately below.
MCrawford (21:25:02)
In this way we can now fill in the rest of the diagram with triplets (very carefully):
MCrawford (21:25:04)

MCrawford (21:25:12)
Adding up the entries at (5, 5) we get 28 + 27 + 28 = 83, our final answer.
MCrawford (21:25:30)
In order to solve this problem we needed to break out counting down in the way that the algorithm broke down the possible routes. Making this leap is essential to understanding how to work with algorithms and recursions (note that breaking the counts into three recursive groups would have been the same as the solution we walked through here).
frodo (21:25:26)
Cool.
MCrawford (21:25:43)
Here is a piece of advice I have on the modern AIME...
MCrawford (21:25:55)
When you get to problem 13 and beyond...
MCrawford (21:26:05)
Don't assume that there is a solution that avoids some grind.
Myself (21:26:01)
There is another way, breaking up the paths by the number of diagonal steps that they have
MCrawford (21:26:37)
There is a casework solution, but it's even uglier and doesn't generalize well.
MCrawford (21:26:52)
Now, let's take a look at 14.
MCrawford (21:27:00)

MCrawford (21:27:05)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-81731438.gif
MCrawford (21:27:10)
How should be begin?
conartist (21:27:19)
i actually tried using graph paper and measuring it out
Mr.Ocax (21:27:21)
draw a diagram
MithsApprentice (21:27:35)
You'll probably need a diagram here. Might as well connect ABCD
peter (21:27:46)
draw a diagram
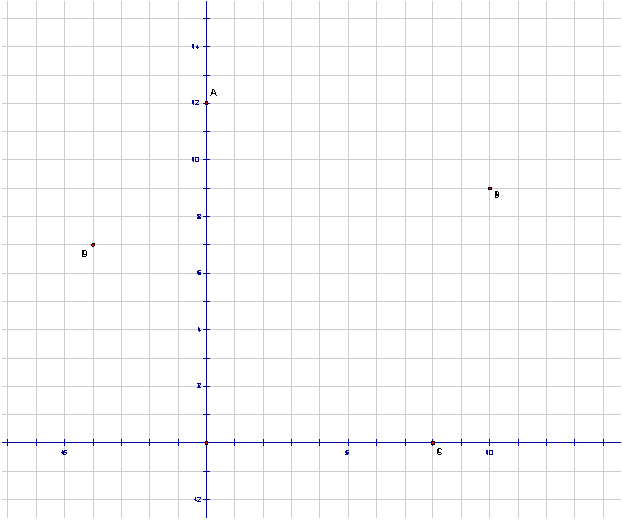
MCrawford (21:28:01)
Let's start with an accurate picture
MCrawford (21:28:03)
MCrawford (21:28:07)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classes/AIME/Images/2005aime1_14_a.gif
MCrawford (21:28:12)
(The pictures for this problem are rather large, so you may want to click on the link to open them in a separate window.)
MCrawford (21:28:28)
What can we observe right away?
Mr.Ocax (21:29:02)
the square is going to be tilted?
Myself (21:29:34)
A and C are on opposite sides; B and D are on opposite sides
MCrawford (21:29:43)
We can see that since AC and BD intersected, the sides containing A and C are parallel, and the same for the sides containing B and D.
pika (21:29:41)
The square cannot have sides parallel to the axes
MCrawford (21:30:02)
How can we find the side length of the desired square?
frodo (21:30:06)
Are the points of the square integral?
MCrawford (21:30:26)
We don't know yet.
Myself (21:30:33)
I think we want to see how much it is rotated by, first
Myself (21:30:55)
I guess we can let the slope of the side containing A be m
MCrawford (21:31:06)
Suppose that the sides containing points A and C have slope m (where m is a positive real number).
This implies that the sides containing points B and D have slope -1/m, since they're perpendicular.
MCrawford (21:31:28)
Let's draw lines of slope m and -1/m through the origin:
MCrawford (21:31:32)
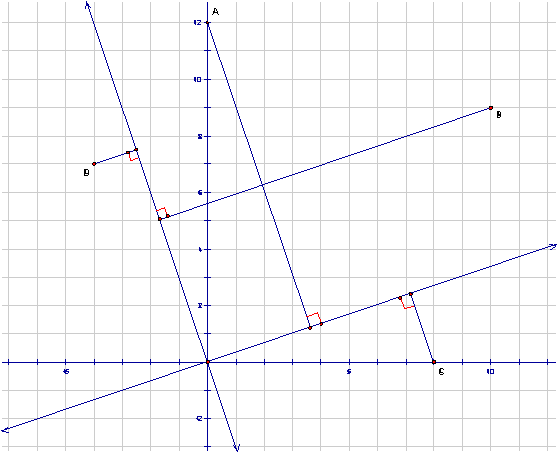
MCrawford (21:31:36)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classes/AIME/Images/2005aime1_14_b.gif
dts (21:30:41)
What I tried was drawing semicircles with radii AB, BC, CD, DA, so that each semicircle sticks out from the middle of ABCD, and each vertex must be on one of the semicircles... didn't get very far, though.
winluo2 (21:31:20)
Maybe draw semicircles with the sides as diameters, since there are right angles.
MCrawford (21:32:04)
There is such a solution involving finding the center of the square. I'll leave that up to discussion on the Message Board.
MCrawford (21:32:15)
Back to our diagram...
MCrawford (21:32:21)
What can we conclude?
aerlinndan (21:32:46)
question: did we just pick an arbitrary m to draw that last diagram?
MCrawford (21:33:13)
Essentially, though our drawing contains an assumption that we'll take care of later...
Myself (21:32:57)
we can find the equations of the lines passing through each side, then see if two sides have the same length
MCrawford (21:33:29)
We can conclude that the length of the side through B (or D) is the distance from A to the line of slope m plus the distance from C to the line of slope m.
Similarly the length of the side through A (or C) is the distance from B to the line of slope -1/m plus the distance from D to the line of slope -1/m.
MCrawford (21:33:33)
We may see this more clearly in the following picture:
MCrawford (21:33:39)
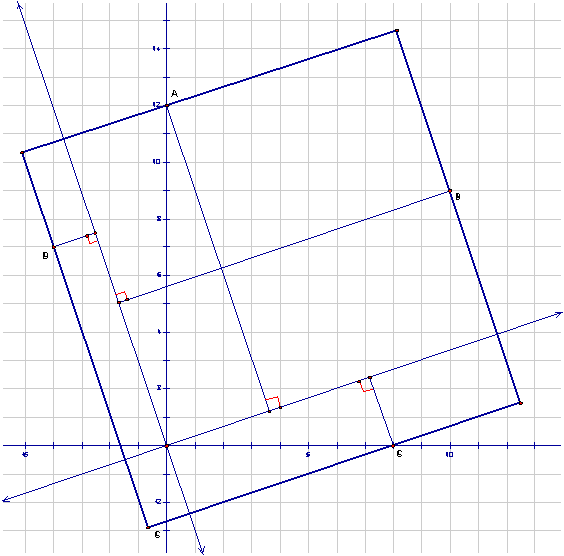
MCrawford (21:33:46)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classes/AIME/Images/2005aime1_14_c.gif
MCrawford (21:33:57)
(Note that we're making some assumptions here: we're assuming that the sides of the square through A and C have positive slope, and that the line of slope m through the origin passes through the square. But when we're done, we'll see that these assumptions are correct.)
MCrawford (21:34:02)
What are the distances from the points A,B,C,D to the respective lines?
Myself (21:34:37)
I wish I knew the formula.... but it would just be a simple application of whatever formlua it is
MCrawford (21:35:10)
The formula for the distance to a line with slope m is something you should learn to derive.
MCrawford (21:35:13)
It's very handy.
pika (21:35:06)
I think you'd need m first.
MCrawford (21:35:24)
We want this in terms of m.
fubu (21:35:21)
(Ax+By+c)/(sqrt(A^2+b^2))
MCrawford (21:35:39)
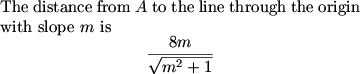
MCrawford (21:35:50)
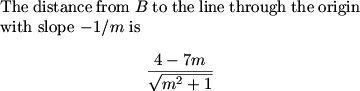
MCrawford (21:36:02)
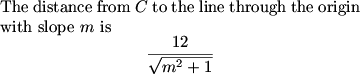
MCrawford (21:36:12)
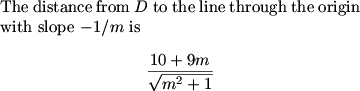
MCrawford (21:36:38)
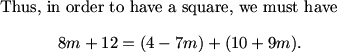
MCrawford (21:36:41)
So what is m?
gibsnson (21:37:01)
1/3
peter (21:37:08)
1/3
MCrawford (21:37:15)
We get that m=1/3.
What's the side of the square?
Bictor717 (21:38:41)
(12+8/3)/(sqrt(10/9))=44/sqrt10
MCrawford (21:38:47)
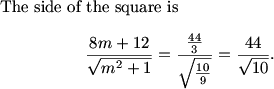
MCrawford (21:39:05)
So the area K of the square is 44^2/10, so 10K = 44^2 = 1936, hence the answer is 936.
MCrawford (21:39:14)
(Note: this solution is based on a solution due to Abhi Gulati, courtesy of AoPS user darktreb.)
MCrawford (21:39:45)
Those of you who know how to use complex numbers in geometry problems could also put this problem on a complex plane and make this solution a bit easier.
kops723 (21:39:48)
so is the comittee's solution uglier?
MCrawford (21:40:19)
It's nicer apparently, though I just heard about it and haven't had a chance to read it.
justdudxit (21:39:51)
Is there a way of using semicircles
MCrawford (21:40:34)
Yes, but carry that discussion to the Message Board.
MCrawford (21:40:45)
Now, let's take a look at the last problem!
MCrawford (21:40:47)

MCrawford (21:40:53)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-35480286.gif
MCrawford (21:41:00)
What is the most important first step in a tough AIME geometry problem?
pika (21:41:11)
DRAW A PICTURE?
MCrawford (21:41:18)
More specific!
Bictor717 (21:41:26)
accurate picture?
Myself (21:41:28)
draw an accurate picture
justdudxit (21:41:29)
Draw a good picture
aerlinndan (21:41:32)
draw a large, accurate picture
Geoffrey (21:41:34)
draw a clear picture where you can write stuff
MCrawford (21:41:48)
We draw the diagram large and as accurately as possible, and label what we know. When I worked this problem for the first time, I was lazy and spent 5 minutes working with a cramped diagram. I then drew it right and had the solution nearly immediately, just because drawing it right made me think about how to draw the diagram, which made me see the solution.
vfiroiu (21:41:44)
label everything
MCrawford (21:42:07)
How do we start when trying to draw the diagram well?
fubu (21:42:37)
trying to get the circle to actual divide the median into three equal lengths..i had a hard time
snare27 (21:42:44)
start with the circle trisecting the line
kops723 (21:42:45)
actually, median first, and then the circle to divide it
MCrawford (21:43:19)
We start with the trisected median CM - from there we can make a rough circle and draw the sides of the triangle tangent to the rough circle. It may take a couple tries, but you should get a decent picture.
MCrawford (21:43:22)
We then do a little labeling - we don't know much, but we do have the midpoint and the trisected segment to work with, and we have this:
MCrawford (21:43:31)
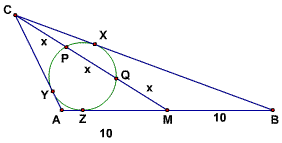
MCrawford (21:43:41)
We want the area of the triangle - what could we find that would give us the area?
dts (21:43:48)
The sides.
kops723 (21:43:51)
height
MCrawford (21:44:05)
We could find the altitude from C, or we could find AC and BC.
Which of these looks more promising and why?
kops723 (21:44:29)
im going to change my mind and say sides--walkaround
snare27 (21:44:32)
find AC and AB, because you can form two triangles wth two equal sides
pika (21:44:44)
AC and BC, because we can try to get those thru <bisector Thrm
Bictor717 (21:44:00)
herons formula, based on the form of the answer they want
MCrawford (21:45:09)
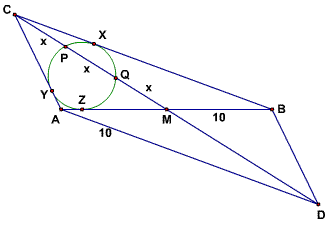
We start off looking for AC and BC, because it seems more likely we'll be able to use our incircle to go after those than to get the altitude from C.
MCrawford (21:45:24)
We have CY = CX, AY = AZ, and BX = BZ, which might be useful.
What tool does this diagram just cry out to try?
justdudxit (21:45:46)
Power of a point
MCrawford (21:46:08)
We have lengths, we want other lengths, and we have tangents and secants. We should try power of a point.
What point should we focus on?
pika (21:46:17)
C?
Bictor717 (21:46:21)
C and M
MCrawford (21:46:36)
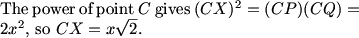
frodo (21:43:54)
Q is the centroid.
dts (21:43:57)
AC= 10, as well.
MCrawford (21:46:59)
What now?
MCrawford (21:47:27)
When we find something that works, the first thing we should do is try it again - maybe it will work again and give us more information.
MCrawford (21:47:35)
We go after the other end of our secant: point M. What do we find?
kostya_4 (21:47:11)
what is power of a point?
aerlinndan (21:47:39)
I'm off to the message boards to learn about what Power of a Point means...
MCrawford (21:48:03)
Yes, please take that discussion to the Message Board.
pika (21:48:02)
2x^2=ZM^2
MCrawford (21:48:14)
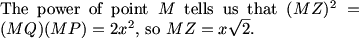
pika (21:47:27)
We have an isoceles
kops723 (21:47:27)
CY=CX
MCrawford (21:48:38)
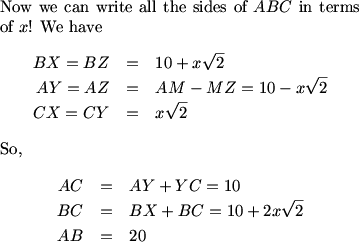
MCrawford (21:48:59)
We know we're close now. We have two of the sides of ABC and the third in terms of x.
What do we do?
pika (21:49:09)
Find x
MCrawford (21:49:24)
Sure, but we're going to need more information.
Bictor717 (21:49:18)
length of median formula, more generally Stewarts Thm
MCrawford (21:49:38)
At this point we may see our way to the solution - we have median CM in terms of x, we have AM = BM = 10, and we know AC and BC in terms of x, so we can just use Stewart to finish. Had we not thought of Stewart immediately, though, we might instead have tried to think of what fact we haven't made use of. This should lead us back to the midpoint (we've used AM and BM, but not the fact that they are equal). This might make us think of how to express the length of a median in terms of its sides.
MCrawford (21:49:58)
To find the length of a median in terms of its sides if we don't know Stewart's Theorem, consider the diagram again:
MCrawford (21:49:59)

pika (21:50:16)
cnc+bmb=dad+man
MCrawford (21:50:40)
If we continue CM to a point D such that ACBD is a parallelogram, what do we know about DM?
gibsnson (21:50:40)
Make it into a parallelogram
Myself (21:51:00)
DM = CM
Bictor717 (21:50:57)
DM=CM
MCrawford (21:51:35)
Which is...?
frodo (21:51:16)
""cynic bombed dads man"" is how I remember Steward's theorem
cczzzing (21:51:46)
3x\
Someone (21:51:47)
3x
kops723 (21:51:50)
3x
gibsnson (21:51:54)
3x
MCrawford (21:52:08)
MCrawford (21:52:16)
The diagonals of a parallelogram bisect each other, so DM = CM = 3x.
How does this help?
dts (21:51:59)
Ah. And the sum of the squares of the sides of a parallelogram is equal to the sum of the squares of the diagonals, so we can get CD directly, and thus get CM.
MCrawford (21:52:31)
The sum of the squares of the diagonals of a parallelogram equals the sum of the squares of the sides of the parallelogram.
In terms of the sides of ABC and median CM, what does this give us?
Mr.Ocax (21:53:23)
36*x^2+400=(10+2xsqrt2)^2+100
MCrawford (21:53:51)
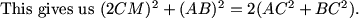
MCrawford (21:53:56)
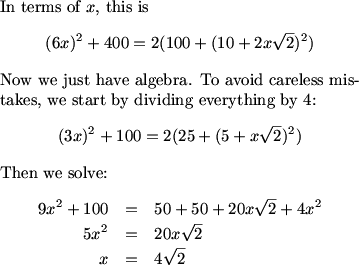
MCrawford (21:54:29)
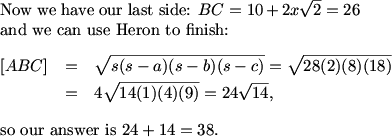
MCrawford (21:55:11)
There is a poll in the AMC for AIME scores.
gibsnson (21:55:02)
Wow, that was surprisingly doable.
MCrawford (21:55:33)
Yes, I think that was a little easier than average for a number 15.
dts (21:55:20)
Overall, what was your opinion on this AIME?
MCrawford (21:56:04)
Slightly on the easy side and there were too many problems with gimmicky math-team shortcuts or assumptions that could be made that made the problems easier.
2005 AIME Math Jam
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.
MCrawford (19:29:21)
The classroom is moderated meaning that students can type into the classroom, but only the moderators can choose a comment to drop into the classroom. This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
MCrawford (19:29:29)
Also, only moderators can enter into private chats with other people in the classroom. You can copy the contents of a private chat by clicking on the notebook icon on the private chat window and copying and pasting the contents into a file on your own computer.
MCrawford (19:29:45)
Finally, the virtual classroom is TeX enabled. TeX allows users to make nice equations and other math expressions. If you would like to learn how to write in TeX/LaTeX, click on the tab on the left side panel of our site and there is a tutorial and reference guide there.
MCrawford (19:29:58)
Using TeX in the virtual classroom is slightly different than using it on the message board or in a TeX editor. If anything you type up in a post that uses TeX then you must use a semicolon (;) to begin your post. For example, if you type
MCrawford (19:30:07)
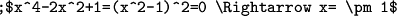
MCrawford (19:30:13)
This message will look like this when posted in the classroom:
MCrawford (19:30:24)
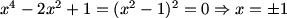
MCrawford (19:30:32)
Just remember, if your post uses TeX, use the semicolon (;) to begin your post!
aaronwysocki (19:30:03)
Quick question: What is the typical combined score you need to get to USAMO?
MCrawford (19:30:53)
That's impossible to know without knowing all the scores including the future scores on the Alternate AIME.
MCrawford (19:31:09)
Problem 1:
MCrawford (19:31:12)

MCrawford (19:31:26)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-227799305.gif
MCrawford (19:31:32)
Where might we begin with a problem such as this one?
towersfreak2006 (19:31:24)
draw a picture! :]
chesspro (19:31:38)
Picture.
justdudxit (19:31:43)
A diagram
sponge008 (19:31:41)
We should draw it...
MCrawford (19:32:01)
A good starting point is a diagram:
MCrawford (19:32:07)

MCrawford (19:32:20)
Now, how can we go about determining the area inside the larger circle and outside the smaller circles?
frodo (19:31:41)
The center of the small circles form a regular hexagon.
aerlinndan (19:32:08)
...and connect the centers of the small circles.
pika (19:31:39)
there's going to be a circle in the center with the same radius as the 6
ChrisChang (19:32:24)
looks like a 7th circle will fit in there
Geoffrey (19:32:29)
good to know that circles can tesselate like hexagons
winluo2 (19:32:29)
Draw radii
towersfreak2006 (19:32:30)
maybe connect all the centers of the little circles? it forms a regular hexagon
MCrawford (19:33:04)
In order to find the answer to this problem, we need to find the area (via the radius) of each smaller circle.
MCrawford (19:33:11)
It is sometimes helpful to connect the radii between tangent circles. In this case a very nice picture emerges:
conartist (19:32:43)
the center to two adjacent points of tangency creates a 60 degree angle
MCrawford (19:33:18)

MCrawford (19:33:21)
What do we know about this hexagon?
Zyloch_2 (19:33:28)
regular
aerlinndan (19:33:30)
Those are six equilateral triangles
sponge008 (19:33:31)
It's regular.
mna851 (19:33:31)
its regular
SoccerBrainy40 (19:33:31)
It's a regular hexagon.
MCrawford (19:33:53)
Due to symmetry we know that the hexagon is regular.
xirtamax (19:33:43)
side of hexagon = diameter of small circle
pika (19:33:51)
The sides are the diameter of the circles
Zratonx (19:33:36)
its side is 2r
frodo (19:33:35)
The side is twice the radius
MCrawford (19:34:16)
We see that the radii of the circles are each half the length of a side of the hexagon. As the hexagon breaks up into 6 congruent equilateral triangle, this means the radii are each half the length of a side of each of the triangles.
vfiroiu (19:33:27)
radius of small circle=10
kky1638 (19:34:05)
Radius of one small circle is 1/3 of the big one!
Zratonx (19:34:20)
so the side+r=30 and the side=2r though 3r=30 and r=10
ChrisChang (19:32:41)
so we can determine the radius of the small circle = 30 / 3 = 10
MCrawford (19:34:51)
We can now see that the diameter of the larger circle is made up of 2 diameters of smaller circles plus two half lengths of the sides of the right triangles. In total, this makes 3 complete diameters of the smaller circles, so the radius of a smaller circle is 30/3 = 10.
MCrawford (19:34:55)
Now, what is the answer to our problem?
RC-7th_? (19:32:42)
Find the area of the large circle, then subtract the combined area of the smaller circles
kky1638 (19:35:11)
thus some of all 6 circle is 600pi
frodo (19:35:09)
30^2pi-6*10^2pi=300pi
Zratonx (19:35:15)
sp 900pi-600pi=300pi or 942
sponge008 (19:35:07)
942
MCrawford (19:35:42)
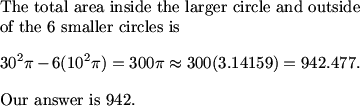
arkajit (19:31:58)
Since the circles are internaly tangent and congruent, they must each be inscribed within 360/60 = 60 degree sectors in the big circle, C. Then, we can see that we have a 30-60-90 triangle with short leg, little r of one of the circles, and hypotenuse (R - r) where R is the radius of the big circle, we can then find the area by subtracting 6 small circles from the big one.
MithsApprentice (19:34:09)
you can inscribe a circle inside the ring of 6 congruent circles that is congruent to each circle in the ring
MCrawford (19:36:05)
Some students might also be aware of the extension of this key symmetry to include a third smaller congruent circle within the ring of 6:
MCrawford (19:36:09)

MCrawford (19:36:21)
This fact makes short work of the problem which goes to show how valuable experience can be in problem solving.
MCrawford (19:36:33)
These kinds of uses of symmetry and relationships between circles are covered in the AoPS Introduction to Geometry class.
mna851 (19:36:20)
On the test would you have to multiply that by 3.14 because no calculators are allowed
MCrawford (19:36:51)
Be careful, you have to express pi to more digits to be sure that your answer is correct on this one.
aerlinndan (19:36:34)
Why is that middle one smaller?
MCrawford (19:37:09)
It's not. Optical illusion.
blahblahblah (19:37:16)
You need 3 sig figs so take 4 sig figs in pi
origamimasterjared (19:36:09)
I used the fact that the angle bisectors/medians of the equilateral triangles cross at 1/3, ; \rightarrow 1\3*30=10 for the small circle radius.
MCrawford (19:37:39)
Let's take a look at problem 2:
MCrawford (19:37:44)

MCrawford (19:37:53)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-253122351.gif
MCrawford (19:38:00)
How might we start with this problem involving variable arithmetic series?
aerlinndan (19:38:12)
Create an explicit formula
rachel (19:38:06)
1+nk=2005
NightFlarer (19:38:09)
write it as 1, 1 + d, 1 + 2d, ...1+xd, so 1 + xd = 2005
pika (19:38:16)
2005=1+k, 1+2k, etc.
MCrawford (19:38:37)
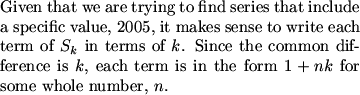
towersfreak2006 (19:38:26)
1, d+1, 2d+1,...,xd+1 or xd+1=2005
solafidefarms (19:38:17)
Subtract 1
chesspro (19:38:20)
1 + k + 2k + ... = 2005
k + 2k + ... = nk = 2004
conartist (19:38:12)
subtract 1 from each of the numbers in the sequence and you have multiples of k
MCrawford (19:39:13)
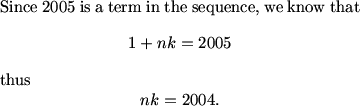
justdudxit (19:38:21)
k=factors of 2004
vfiroiu (19:38:27)
we need to find the factors of 2004
wild octagon (19:38:36)
factor 2004
flierdeke (19:38:38)
so nk = 2004.
rachel (19:38:39)
factors of 2004
smiley_2 (19:38:51)
Factor 2004, because 2004=nk
ChrisChang (19:38:52)
factors of 2004
MCrawford (19:39:39)
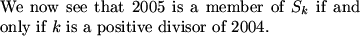
MCrawford (19:39:50)
Before we go on.
MCrawford (19:39:56)
I have a request.
MCrawford (19:40:14)
This Math Jam is getting very large. If you plan to post, please post succint ideas as concisely as possible.
MCrawford (19:40:29)
I will not have time to read all of the hundreds of posts.
MCrawford (19:40:32)
What is the number of positive divisors of 2004?
arkajit (19:39:37)
We know that to reach 2005, the sequence must increase in some integer amount of steps by 2004, thus we are looking for the number of divisors of 2004; we prime factorize and then we use the fact that p^n where p is prime and n is an integer will yield n + 1 divisors and we multiply by all such n - we have 2004 = 2^2 * 3 * 167; thus we have (2+1)(1+1)(1+1) = 12
conartist (19:39:37)
prime factorize 2004, raise powers +1 and multiply
vfiroiu (19:39:45)
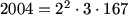
sponge008 (19:39:47)
2004=2^2*3*167
rachel (19:39:47)
3*2*2=12 factors
sponge008 (19:39:57)
So 3*2*2=12
frodo (19:39:57)
167*3*2^2=2004 There are 2*2*3=12 factors.
MCrawford (19:41:15)

MCrawford (19:41:28)
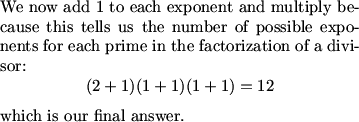
MCrawford (19:41:39)
There were two main keys to unlocking this problem. First, we needed to write the general form of a term of each arithmetic series. From there we did a tiny bit of manipulation to recognize the divisor counting problem within.
MCrawford (19:41:48)
Many kinds of divisor counting problems are covered in the AoPS Introduction to Number Theory class and basic algebraic manipulations of equations in integers will be covered in the Intermediate Number Theory class.
MCrawford (19:41:59)
Now, let's take a look at problem 3.
MCrawford (19:42:11)
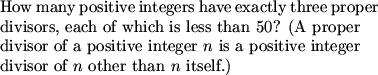
MCrawford (19:42:17)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-30557481.gif
MCrawford (19:42:29)
How can we begin with this problem?
krustyteklown (19:42:28)
3 proper divisors means 4 real divisors
Zratonx (19:42:44)
look for numbers with 4 factors
justdudxit (19:42:44)
The number actually has 4 factores
MCrawford (19:42:55)
First, we note that an integer with 3 proper divisors has a total of 4 divisors.
chesspro (19:42:34)
They're in the form:
x^3
x^1 * y^1
white_horse_king88 (19:43:05)
Form 1,x,y,xy, or 1,x,x^2,x^3. X and y are prime.
Zratonx (19:43:13)
use prime factorization backwards
pika (19:43:18)
x^3 or xy
fubu (19:43:19)
x, y must be primes
MCrawford (19:43:47)

MCrawford (19:44:11)
We can now break the problem into the two cases for the forms of the integers we are looking for.
MCrawford (19:44:28)
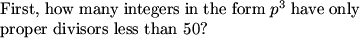
snare27 (19:44:39)
4
snare27 (19:44:41)
2, 3, 5, 7
vfiroiu (19:44:45)
4
RC-7th_? (19:44:46)
2,3,5, and 7 could be p, so 4
Mr.Ocax (19:44:46)
2^3, 3^3, 5^3, 7^3
MCrawford (19:45:41)
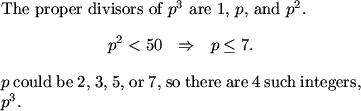
Zyloch_2 (19:45:13)
since 7^2 still < 50
vfiroiu (19:45:33)
2&4, 3&9, 5&25, 7&49
pika (19:45:22)
err, 7 squares less than 50, 4 primes
MCrawford (19:46:15)
frodo (19:45:49)
The primes are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, and 47.
Zyloch_2 (19:43:36)
15 prime #s under 50
Derek (19:43:42)
list the prime numbers from 1 to 50
vfiroiu (19:43:59)
find the number of primes lass than 50
rachel (19:45:21)
2 primes: 15*14/2=105
Derek (19:46:22)
15 C 2
thinkingmachine (19:46:22)
15 choose 2
rachel (19:46:27)
15x14/2=105
RC-7th_? (19:46:25)
The are 15 primes less than 50, so C(15,2)=105
xirtamax (19:46:28)
15C2
crazygeniuskid (19:46:30)
15C2
MCrawford (19:47:08)
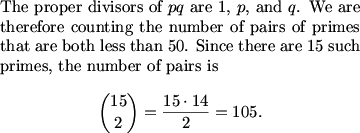
RC-7th_? (19:43:28)
If the number has 3 proper divisors, it has 4 factors. So it must be of the form p*q or p^3, where p and q are prime. Then we look at the primes under 50 for p*q. There are 15 primes, so there are C(15,2) numbers of the form p*q that satisfy the condition. Then we look at p^3, see that p^2 is less than 50, so it could be 2,3,5 or 7. 4+105=109
arkajit (19:45:27)
now we can list primes and see how many we want; there are 15 primes less than 50 and we can choose only two; and they're are 4 primes whose square is less than 50 - so we have 15 C 2 + 4
rachel (19:47:05)
105+4=109
thinkingmachine (19:47:22)
added to 4 gives the answer of 109
smiley_2 (19:47:31)
105+4=109 total.
MCrawford (19:47:55)
MCrawford (19:48:06)
The keys to this problem were understanding how to count the number of divisors of an integer well enough to break this problem into cases and then knowing how to count within those cases in an organized way.
kky1638 (19:48:02)
that is cool solution
MCrawford (19:48:19)
These are skills that the AoPS Introductory Number Theory and Counting & Probability classes focus on.
thinkingmachine (19:48:19)
can we go over number 14?
MCrawford (19:48:31)
We're going over all the problems in order.
MCrawford (19:48:38)
Now, let's take a look at number 4.
MCrawford (19:48:51)

MCrawford (19:49:07)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-245314190.gif
MCrawford (19:49:15)
What is the first thing we need to do with this problem?
fubu (19:49:16)
n=number of people, n=a^2+5, n=c(c+7)
rachel (19:49:24)
write eq
thinkingmachine (19:49:25)
set up two equations
solafidefarms (19:49:27)
Write it in an equation
MCrawford (19:49:55)
The first thing we need to do is translate the words into math.
rachel (19:49:03)
a(a+7)=b^2+5
Mr.Ocax (19:49:15)
so x(x+7)=y^2+5, and we solve for x using the quadratice formula
pika (19:49:16)
x^2+5=y(y+7)
solafidefarms (19:49:17)
k(k+7)=n^2+5
sponge008 (19:49:19)
x^2+5=y(y+7)
Bassooner (19:49:20)
x^2+5=c^2+7c
snare27 (19:49:31)
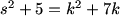
conartist (19:50:08)
y < X < y+7
MCrawford (19:50:34)
MCrawford (19:51:01)
MCrawford (19:51:14)
What's the easier part of this equation to focus on?
fubu (19:50:47)
you can create then a quadratic equation, and use the discriminant to restrict values since the discriminant must be a square of an integer
MCrawford (19:51:38)
I didn't do that, but it might be easier than what I did.
justdudxit (19:51:25)
LHS
rachel (19:51:28)
a^2+5
MCrawford (19:51:48)
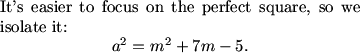
thinkingmachine (19:51:50)
what's LHS?
MCrawford (19:52:00)
left hand side
vfiroiu (19:51:18)
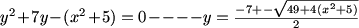
MCrawford (19:52:20)
I haven't followed this solution out, but it may be quicker.
MCrawford (19:52:30)
Now what?
frodo (19:50:19)
Complete the square first?
frodo (19:52:38)
Could you complete the square?
MCrawford (19:52:51)
How exactly?
dbkhoa (19:52:50)
you have to multiple both side by 2
MCrawford (19:53:05)
We could, but it's not necessary.
Bictor717 (19:53:05)
Multiply by 4 to avoid fractions
dbkhoa (19:52:07)
(2a)^2 +69 = (2m+7)^2
MCrawford (19:54:01)
Ah, yes, multiplying by 4 was nice indeed.
MCrawford (19:54:05)
What have we learned here?
frodo (19:54:07)
take the difference of squares next
RC-7th_? (19:54:21)
We can use difference of squares.
dbkhoa (19:54:27)
69=(2m+7-2a)(2m+7+2a)
Zratonx (19:54:28)
two perfect squares with a difference of 69
kostya_4 (19:54:46)
69=3*23
mna851 (19:54:51)
Decompose
mna851 (19:54:53)
69
MCrawford (19:55:09)
Now what?
RC-7th_? (19:55:07)
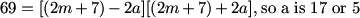
pika (19:55:18)
2m+7-2a=3
2m+7+2a=23
MCrawford (19:55:37)
This gives the 5.
MCrawford (19:55:47)
Where does the 17 come from?
dbkhoa (19:55:14)
but we need the maximum a, so it should be 1*69
MCrawford (19:56:09)
The same equations = 1 and 69 give a = 17.
krustyteklown (19:56:09)
2m+7+21=69
RC-7th_? (19:55:54)
2m+7-2a=1 and 2m+7+2a=69
Yagmoth0000 (19:56:12)
i
Someone (19:56:16)
m=3
justdudxit (19:56:16)
Why can't 69 = 1*69
dbkhoa (19:56:07)
2m+7+2a=69
2m+7-2a=1
pika (19:56:05)
use 1 and 69 instead of 3 and 23
RC-7th_? (19:50:53)
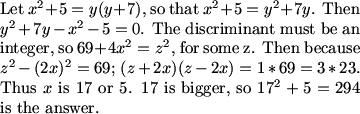
fubu (19:53:56)
i did c^2+7c-(a^2+5)=0, so discriminant is 49+4a^2+20, which is equal to some integer, m, squared, so 4a^2+69=m^2, m^2-4a^2=69, so (m+2a)(m-2a)=69=1*69=2*23, the maximum will use 1 and 69 so m=35, a=17. so the maximum of n = 17^2+5=294
RC-7th_? (19:56:53)
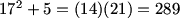
fubu (19:57:03)
m=35, a=17
kky1638 (19:57:05)
add 2 eq.
frodo (19:57:09)
Thus 17^2+5=294
MCrawford (19:57:24)
294 is indeed the answer.
MCrawford (19:57:36)
Probably most students who got the right answer on this problem plugged in numbers until they found the right answer. That just goes to show that grinding out calculations can sometimes help with a problem.
MCrawford (19:57:42)
Soon AoPS plans to offer an Intermediate Number Theory course which will cover, among other things, equations involving integers and divisibility considerations.
MCrawford (19:58:04)
It's fortunately looking like this will take less than 3 hours!
MCrawford (19:58:10)
Let's move to number 5 now.
MCrawford (19:58:20)

MCrawford (19:58:31)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-107057566.gif
Mr.Ocax (19:58:33)
oo.. i personaly enjoyed this one
MCrawford (19:58:48)
What is interesting about this counting problem?
krustyteklown (19:58:41)
first consider only faces, then consider coloring of coins
justinian (19:58:47)
find the possible ways of arranging the color of coints, and the ways of arranging the faces
fubu (19:58:47)
find out how many ways you can arrange the colors first before you find out how many ways to arrnage the face up /face down's
dbkhoa (19:58:57)
just forget the face first
aerlinndan (19:59:03)
Can we consider this problem two separate parts: the colors part and the face-up or face-down part?
MCrawford (19:59:32)
This counting problem involves two independent counting tasks. We need to find the number of possible orders of the 8 coins and also the number of ways each order can be arranged such that coins are never face to face.
MCrawford (19:59:51)
How many possible orders are there for the 8 coins?
RC-7th_? (19:58:48)
First look at the coins as indistingusible, then multiply by C(8,4)=70
frodo (19:58:50)
There are C(8,4) ways to arrange coins regardless of position.
ChrisChang (19:59:01)
we can symbolize this: gold coins are ""a"" and silver are ""b"", so we are mixing up aaaabbbb
Bassooner (19:59:12)
use pascal's triangle to find that the number of possible arrangements of just silver and gold coins, no matter what facing, which is 70.
fubu (19:59:47)
there are 8!/(4!4!)=70 ways to arrange color only
MCrawford (20:00:30)
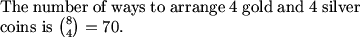
MCrawford (20:00:50)
Now, in how many ways can any one sequence of gold and silver coins be stacked such that no two coins are face to face?
conartist (19:59:09)
9 ways of arranging the faces
thinkingmachine (19:59:21)
number of ways to arrange 8 coins not counting heads up or down is (8 choose 4)
and then the number of ways to arrange heads up and heads down is 9
snare27 (19:59:22)
Isolating the arrangments of the faces of the coins, they can be stacked so that 0 through 8 of the coins face either directions, totaling to nine arrangements regardless of color.
vfiroiu (19:59:31)
face-wise, there are 9 different arrangements-1st coin facing up, 2nd coin up, 3rd.......8th coin up or all coins down
Mr.Ocax (20:00:14)
then there are 9 ways to place them so they aren't face together
Bassooner (20:00:52)
DDDDDDDD
DDDDDDDU
DDDDDDUU
DDDDDUUU
DDDDUUUU
DDDUUUUU
DDUUUUUU
DUUUUUUU
UUUUUUUU
is the different number of facings, so the number of face arrangements is 9
snare27 (20:01:20)
There are 9 ways, because each stack can have the bottom 0 through 8 coins face down
MCrawford (20:01:39)
When stacking the coins from bottom to top, we can never go from a face up coin to a face down coin. Since the coins can never switch back to face down after they are face up, there is at most one switch between face up/down (from down to up). There are two stacks without a switch (all up or all down) and 7 places between coins where a switch could occur. This means there are 9 possible up/down states for the coins.
MCrawford (20:01:51)
Really we could just think of the possible switch points as including the spaces before or after the coins, so there are 8 + 1 = 9 possible switch points.
MCrawford (20:01:55)
What is our final answer?
peter (19:59:09)
9 head-tail combinations, C(8,4) ways to order silver and gold, so 9*C(8,4) = 630
rachel (19:59:24)
8C4 *9 =630
Mr.Ocax (20:00:21)
so 70*9=630
rachel (20:00:43)
8C4 *9=630
chesspro (20:01:01)
We can pick any number from 0 to 8 coins to be facing down, so 70 * 9 = 630.
Bassooner (20:01:10)
9*70=630
RC-7th_? (20:01:22)
9*70=630
frodo (20:01:27)
70*9=630
vfiroiu (20:01:38)
9*70=630 different ways
conartist (20:01:40)
9*70=630 total ways
smiley_2 (20:01:53)
9*70=630
MCrawford (20:02:44)
Geoffrey has a nice way to wrap this up into one problem!
Geoffrey (20:01:59)
hey. if we consider the flip from down to up as |, isn't it just the number of permutations of GGGGSSSS|?
MCrawford (20:03:30)
It is important to analyze the interesting facets of a problem. Once we broke this problem into two and recognized the independence of the two parts, the calculations were not that difficult.
Bictor717 (20:03:12)
9!/(4!4!)=630, neato
sponge008_2 (20:03:12)
Wow, that is really elegant!
justinian (20:03:45)
hmm, that's nice
Sly Si (20:03:47)
Neat!
MCrawford (20:04:00)
This problem is similar to some problems covered in the AoPS Counting & Probability classes.
MCrawford (20:04:15)
Moving on to problem 6.
thinkingmachine (20:04:14)
advertising all the way, eh???
MCrawford (20:04:46)
To be sure, the school and the books fund the entire site and the Math Jams are a way to find students capable of this caliber of problem solving.
miraculouspostmaster (20:04:47)
durn straight
thinkingmachine (20:04:58)
just kidding, i take that back...
MCrawford (20:05:09)
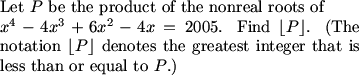
MCrawford (20:05:16)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-39478121.gif
MCrawford (20:05:24)
What is interesting about the given equation?
miraculouspostmaster (20:05:20)
ooh oooh add 1!
chesspro (20:05:23)
Add one and factor.
pika (20:05:30)
Add 1 to make (x-1)^4=2006.
alan (20:05:35)
add 1 and factor into (x-1)^4=2006
corpulus (20:05:37)
it's a binomial expansion
MithsApprentice (20:05:41)
binomial coefficients
conartist (20:05:35)
almost fourth power
WarpedKlown1335 (20:05:35)
It's a binomial expansion.
snare27 (20:05:28)
Noticing the the coefficients look like a row of Pascal's Triangle, add one to each side of the equations. Then factor it into (x-1)^4=2006.
MCrawford (20:07:16)
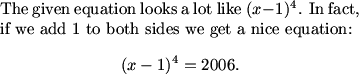
MCrawford (20:07:34)
Now how do we analyze the nonreal roots?
justdudxit (20:06:31)
Its like roots of unity...
pika (20:06:08)
fourth roots of 2006
vfiroiu (20:06:31)
permutations of 1, -1, i and -i
frodo (20:06:56)
Find the four fourth roots of 2006.
MCrawford (20:08:28)
Do we need all four?
joml88 (20:07:29)
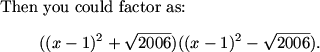
RC-7th_? (20:07:31)
Take the fourth root of both sides to get x-1=2006^(1/4). However, we're not only looking at real roots, so x-1 equals 2006^(1/4) or 2006^(1/4)*i or -2006^(1/4) or -2006^(1/4)*i. But we only need to look at the roots with i in then.
conartist (20:07:48)
nonreal comes in conjugates
MCrawford (20:08:57)

WarpedKlown1335 (20:07:52)
The nonreal roots will be the roots of the equation (x-1)^2 = -sqrt(2006)
chesspro (20:07:54)
Square root it, toss out the positive root, expand, and you have product of roots.
dbkhoa (20:08:09)
(x-1)^2=+/-sqrt(2006)
pika (20:06:41)
x-1=+-fourthroot(2006);+-i*fourthroot(2006)
mna851 (20:07:16)
Subtract the 2006 and do the difference of two squares. Factoring the (x-1)^2+2006=0 Will give you nonreal roots.
MCrawford (20:10:04)
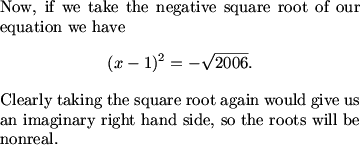
MCrawford (20:10:23)
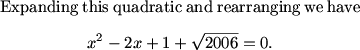
pika (20:07:46)
floor (1+sqrt2006)
dbkhoa (20:10:16)
for the non-real roots, it'll be the roots of x^2 -2x+1+sqrt(2006)=0
MCrawford (20:11:08)
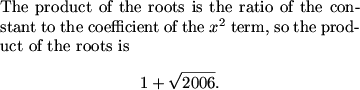
justdudxit (20:10:52)
P = 1+rad(2006) => 45
fubu (20:09:36)
ohh..i did ((x-1)^2-sqrt2006)((x-1)^2+sqrt2006)=0, so we know (x-1)^2+2006 =0 will give non real roots so that becomes x^2-2x+1+sqrt2006=0, so the products will be 1+sqrt2006, since int(sqrt2006) is 44, then the answer is 45
mna851 (20:10:46)
Viete's theorem c/a
MCrawford (20:11:54)

fubu (20:11:31)
floor(sqrt2006)is 44 so floor (1+sqrt2006) is 45
pika (20:11:32)
floor that is 45
MCrawford (20:12:15)
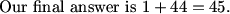
rachel (20:08:47)
I found the product of all roots and divided by the product of real roots
corpulus (20:08:56)
you can divide the product of the roots by the two real roots
MCrawford (20:12:47)
That's certainly an option.
MCrawford (20:12:52)
The key to working this problem efficiently was noticing that we had a nice way of manipulating the algebra without trying to hunt down the actual roots to the fourth degree polynomial. It pays to be aware of common binomial coefficients and how to use them.
MCrawford (20:13:03)
It was also important to recognize that taking the square root immediately separately the polynomial into two quadratics with real and unreal roots respectively. This reduced our problem to a problem of two variables that was far more tractable.
MCrawford (20:13:12)
This problem is similar to some that we work in the Intermediate Algebra class.
MCrawford (20:13:34)
Problem 7:
MCrawford (20:13:38)
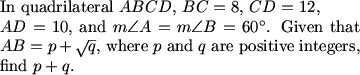
MCrawford (20:13:41)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-29759086.gif
MCrawford (20:13:53)
Where should we start with this one?
sponge008_4 (20:13:50)
We need a diagram...
Someone (20:13:51)
draw diagram
RC-7th_? (20:13:53)
Draw a picture!
alan (20:13:56)
draw picture!
conartist (20:13:57)
diagram
mna851 (20:13:59)
Draw a picture of course
MCrawford (20:14:21)
It's always good to start with a nice, clean, easy to view diagram -- EASY TO VIEW. The difference between seeing through a problem such as this one is often the difference between being able to read information into your own diagram.
MCrawford (20:14:24)

MCrawford (20:14:40)
What is interesting about the diagram?
pika (20:14:25)
use the 60degrees!
sponge008_4 (20:14:51)
It's almost isoceles...
fubu (20:14:53)
the 60 degree angles.
kops723 (20:14:58)
there are 2 60 degrees
dts (20:14:59)
60 degree angles... begging for 30-60-90.
MCrawford (20:15:38)
The twin 60 degree angles look interesting.
arkajit (20:14:03)
break it into an isosceles trapezoid and triangle
krustyteklown (20:14:01)
extend DC and AD to form an equilatrel triangle
MCrawford (20:16:13)
Both good approaches. I took the first.
MCrawford (20:16:18)
If we draw a segment from C to AD parallel with AB we have an isosceles trapezoid:
MCrawford (20:16:26)

MCrawford (20:16:29)
Here I went ahead and filled in angle information. This is an important step in working with any diagram (and another reason to make your diagram big enough to work with).
snare27 (20:13:54)
Draw altitudes from points C and D, making two 30-60-90 right triangles
Mr.Ocax (20:14:08)
and you will have 30-60-90 triangles
pika (20:14:37)
create 30-60-90 triangles!
conartist (20:14:37)
drop altitudes to AB from d and C
conartist (20:14:57)
you can construct many right triangles
ChrisChang (20:15:02)
we can make 30-60-90 triiangles
sponge008_4 (20:15:15)
Oh, we have an is. trap, and a tri
MCrawford (20:17:48)
We can now drop altitudes from C and E to AB giving nice 30-60-90 right triangles with which to work:
MCrawford (20:17:51)

MCrawford (20:18:10)
We see that the smaller legs are half each hypotenuse and are of length 4.
chesspro (20:16:50)
Law of cosines.
arkajit (20:17:14)
and use law of cosines on the triangle to find EC
Someone (20:15:43)
law of cosines any good here?
arkajit (20:18:19)
and EC will equal the missing piece we need to find AB
MCrawford (20:19:33)
We see that AB is 8 more than EC due to the nice rectangle that sprang up in our diagram.
MCrawford (20:19:38)
We can see that angle CED is 60 degrees giving us the opportunity to apply the law of cosines to the problem.
vfiroiu (20:19:17)
what if u dont know trig like me?.....
guangweicao (20:18:49)
instead of laws of cosines, draw a perpendicular from D to AB
guangweicao (20:18:56)
its much easier and does not require trig
MrsB (20:19:57)
If you darw 30-60 90 to D instead of e it works out beautifully
snare27 (20:19:45)
I dropped the altitudes directly from C and D, and then made a third right trianle by extending a line from C perpendicular to the existing right triangles. This triangle had a hypotenuse of 12 and on leg equal to the difference if thte legs of the two 30-60-90 triangles.
MCrawford (20:20:42)
I tend to seek out symmetries with Geometry problems, so it is likely I did not find the solution with the lowest level of machinery.
lotrfan (20:19:26)
4+x^2-2x=144, x=EC
MCrawford (20:20:53)
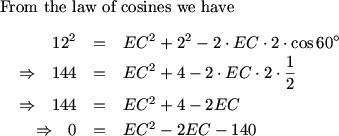
pika (20:20:40)
Yes, so length of AB is 9+sqrt(141)
MCrawford (20:21:38)
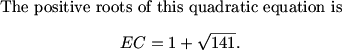
fubu (20:18:10)
using the equilateral triangle method, we label AB=x, label the point where the extensions of AD and BC meet as E, so ED=x-10 and CE=x-8. since <E=60 degrees, we can use the law of cosines. so 144=(x-8)^2+(x-10)^2-2(x-8)(x-10)*1/2, after algebra we find that x=9+sqrt141 so the answer is 150
peter (20:20:29)
I dropped perpendiculars from D and C to AB at points E and F, then from C to DE at G, so DE is 5rt3 CF is 4rt3, so DG is rt3, so CG is rt141, because DEFC is rectangle, AB is 9 + rt141, so answer is 150
Mr.Ocax (20:21:33)
so 141+9=150
MCrawford (20:22:35)
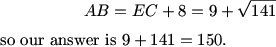
MCrawford (20:23:27)
The key to solving this problem was recognizing the interesting feature of the initial diagram, namely, the twin 60 degrees angles that allowed us to draw a nice isosceles trapezoid into our diagram. From there, the angle work was nice and we simply needed to apply the law of cosines to get the length of EC.
MCrawford (20:23:37)
Recognizing the interesting feature of a diagram is taught in all of the AoPS Geometry classes and the law of cosines is discussed in length in the AoPS Intermediate Trigonometry/Complex Numbers class.
conartist (20:19:44)
another way is if you drop the altitudes from D and C onto AB, you would have the right triangle containing DC to have side of rad3 and a hyp of 12. and apply pythagorean thereom.
ginasboys (20:21:25)
Um. from the way I did. I dropped an atltitude from D to AB (at F), and then another altitude from C to DF. Then DEC is a right triangle. So no LoS is used and it's purely elementary Pathygorem thms...
MrsB (20:21:27)
Get d's Perpendicular is 5rt3 and C's perpendicular is 4rt3, so side on top triangle is 1rt3
Sly Si (20:21:40)
I solved it using the equilateral triangle method--the existence of a 30-60-90 triangle never even occurred to me!
krustyteklown (20:22:49)
did same as fubu
vfiroiu (20:16:16)
i had AD and BC connecting at the bottom to get an equilateral triangle
dts (20:17:56)
Drop perpendiculars DF and CG to AB, then drop a perpendicular from C onto DF. The answer is simple from here.
kky1638 (20:23:28)
so we can do this without trig.
MCrawford (20:24:19)
Indeed, my solution was not the simplest.
MCrawford (20:24:33)
Dave Patrick is now going to take over for a couple of problems.
DPatrick (20:24:46)
Hi
DPatrick (20:24:48)
Problem 8:
DPatrick (20:24:51)

DPatrick (20:24:56)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-53367102.gif
RC-7th_? (20:25:03)
Replace 2^(111x) with y
thinkingmachine (20:25:07)
let b = 2^(111x)
peter (20:25:08)
substitute y for 2^111x
Mr.Ocax (20:25:09)
could we do y=2^111x?
lotrfan (20:25:18)
Definitely suggests a substitution.
Myself (20:25:29)
it seems as if substituting 2^(111x)=y would work well here
DPatrick (20:25:42)
The most obviously interesting aspect of the given equation is that the exponents involve 111x, 222x, and 333x. This gives a rather ugly equation.
DPatrick (20:25:54)
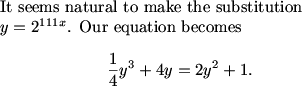
DPatrick (20:26:05)
Now, what exactly do we want out of this equation?
thinkingmachine (20:26:24)
find the products of the roots
frodo (20:26:26)
The product of y's roots.
dts (20:26:26)
The product of the solutions for y, since that gives us the sum of the solutions for x.
dbkhoa (20:26:52)
we want y1*y2*y3
DPatrick (20:27:16)
It is easy to jump to thinking that we now want to find the sum of the roots of our new equation, but there is something wrong with this idea.
DPatrick (20:27:23)
DPatrick (20:27:39)
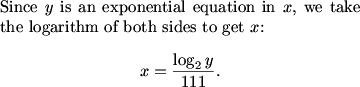
DPatrick (20:27:51)
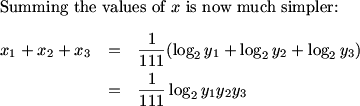
dbkhoa (20:27:38)
because 111(x1+x2+x3)= log(2)(y1)+log(2)(y2)+log(2)(y3)
ginasboys (20:27:19)
Since we make the substitution 2^111x = y, or log2 y ./ 111 =x. Consider 3 solutions x_1, x_2, and x_3. We are interested in log2 (y_1 *y_2 * y_3). Or the product of roots.
DPatrick (20:28:24)
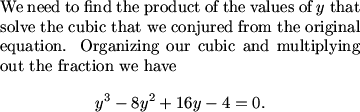
DPatrick (20:29:04)
What is the product of the roots?
frodo (20:28:27)
rachel (20:28:49)
product of roots =4
Someone (20:29:09)
product=4
justdudxit (20:29:13)
4
pika (20:29:14)
4
sleepsta (20:29:15)
4
smiley_2 (20:29:16)
4
DPatrick (20:29:29)
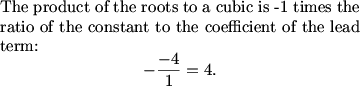
DPatrick (20:29:36)
What is our final answer?
ginasboys (20:29:43)
2/111
frodo (20:29:48)
2/111 2+111=113
kops723 (20:29:50)
2/111
ginasboys (20:29:50)
2/111 => 113
justdudxit (20:29:51)
2/111 => 113
dbkhoa (20:29:52)
2/111
flierdeke (20:29:55)
113
DPatrick (20:30:08)
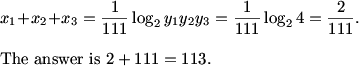
DPatrick (20:30:22)
This problem is a great example of how identifying the ugly aspect of an equation can lead us down the best solution path. Here we employed a nice substitution that gave us a much cleaner equation to work with. However, we still had to recognize the relationship between the variables as we applied the exponential function in our substitution. Find the sum of the roots of the original equation meant using the inverse of the exponential function (logarithms) to relate the original problem to the new equation.
DPatrick (20:30:33)
These kinds of substitutions and functional considerations are covered in the AoPS Intermediate Algebra class.
DPatrick (20:30:44)
Problem 9:
DPatrick (20:30:47)
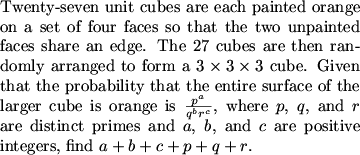
DPatrick (20:30:56)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-212577278.gif
DPatrick (20:31:10)
What about this problem gives us a reasonable starting point?
rachel (20:31:13)
3 cases, 1-3 faces showing
vfiroiu (20:31:21)
3 cases: cube on surface, on edge, or on corner
Myself (20:31:27)
8 corners, 12 edges, 6 faces 1 center cube
DPatrick (20:31:48)
The larger cube is made up of 1 cube in the very center, 6 in the centers of each face, 12 in the middles of edges, and 8 at the corners of the large cube.
DPatrick (20:32:02)
Our classification of the way the cubes are arranged helps us because each of the smaller cubes are the same and we now recognize that instead of viewing the problem as 27 different problems, we can now view the problem as 3 problems (we toss out the cube in the very center because its painting orientation is irrelevant).
DPatrick (20:32:18)
Now, what is the probability that a cube in the center of a face of the larger cube shows only orange?
ChrisChang (20:32:19)
can we ignore the center cube?
DPatrick (20:32:52)
Yes, because it's orientation doesn't affect the outside of the big cube at all.
peter (20:32:33)
4/6
rachel (20:32:36)
2/3
kops723 (20:32:36)
4/6=>2/3
mna851 (20:32:38)
2/3
Mr.Ocax (20:32:41)
2/3?
Geoffrey (20:32:47)
4 good / 6 possible = 2/3.
flierdeke (20:32:50)
4/6 = 2/3
frodo (20:32:52)
2/3
pika (20:32:56)
4/6 chance
DPatrick (20:33:11)
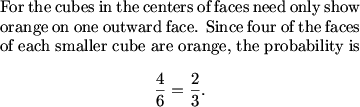
DPatrick (20:33:30)
Now, what can we do to help us determine the probability that a smaller cube on an edge of the larger cube shows only orange?
DPatrick (20:33:53)
A model might help us here:
DPatrick (20:33:59)

DPatrick (20:34:10)
Thinking about the cubes as dice might help us. This helps us model the fact that the unpainted faces are adjacent which is essential to getting the right answer.
We will let the unpainted faces be the ones labeled 1 and 2.
DPatrick (20:34:32)
Now, how many orientations are there for the cube (in terms of the numbers)?
kops723 (20:34:45)
24
ChrisChang (20:34:54)
24
justdudxit (20:35:02)
24
MPS-vras (20:35:06)
24
DPatrick (20:35:23)
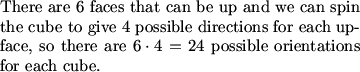
DPatrick (20:35:34)
For how many of those orientations will both (adjacent) exposed faces of the cube be orange?
DPatrick (20:37:08)
There are several ways we could perform this count, but complementary counting works for us. We can count the number of ways in which at least one unpainted face is exposed:
DPatrick (20:37:13)

DPatrick (20:37:20)
Suppose the two exposed faces are where the 1 and 2 are in this picture.
There are 2 orientations in which both unpainted faces are exposed.
DPatrick (20:38:02)
How many orientations expose one painted face and one unpainted face?
frodo (20:37:58)
12 with just one.
pika (20:38:31)
12
DPatrick (20:38:45)
Right, there are 2 places one unpainted face could be exposed and 2 unpainted faces that could occupy those places. For each of those circumstances there are 3 orientations such that the other exposed face is painted (discounting the fourth orientation in which both unpainted faces are exposed).
DPatrick (20:39:03)
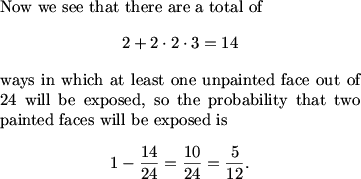
DPatrick (20:39:18)
There are other ways we could have come up with this probability.
DPatrick (20:39:32)
We could have directly counted the number of orientations with both painted faces exposed.
DPatrick (20:39:37)
Or, we could have focused on edges, as such:
thinkingmachine (20:35:55)
it's just the number of edges not touching an unpainted face... since there are 7 such edges, we have 12 - 7 for a total of 5 such orientations
DPatrick (20:40:14)
Now how can we determine the probability that a small cube at the corner of the large cube will have only orange faces exposed?
Someone (20:40:36)
it must have 3 faces exposed
Mr.Ocax (20:40:59)
only 2 ways to place it
Sly Si (20:41:01)
The vertex that serves as the vertex of the large cube must border three orange faces. There are two such vertices, so the probability is 2/8=1/4.
DPatrick (20:41:35)
Right -- the positioning of a corner cube is determine by the vertex that forms the corner of the big cube.
DPatrick (20:41:55)
Only 2 of the 8 vertices of the small cube lie where 3 orange faces meet.
DPatrick (20:42:07)
So the probability is 2/8 = 1/4.
DPatrick (20:42:17)
Now, how do we determine the final answer?
white_horse_king88 (20:42:55)
Raise each to the power of the number of cubes there are with the certain number of exposed faces.
ginasboys (20:43:00)
There are 8 corners, 12 edges, and 6 centers. Thus (1/4)^8 * (5/12)^12 * (2/3)^6 is our desired probability.
dbkhoa (20:43:02)
power each of the posibilities to the number of small cubes
RC-7th_? (20:42:42)
So we have (5^12)/(2^34*3^18), so we have 5+12+2+34+3+18=74
rachel (20:43:09)
(2/3)^6*(5/12)^12*(1/4)^8, cancel 2s, add components to get 74
lotrfan (20:43:10)
cancel stuff out and split up according to the form given in the problem after multiplying the probabilities raised to the power representing the number of times that type of cube occurs.
DPatrick (20:43:28)
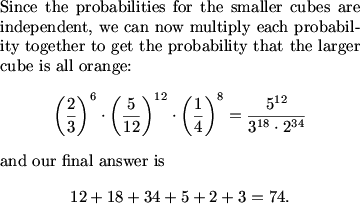
DPatrick (20:43:46)
This problem tested our ability to organize independent probabilities into cases and also find a way to model the orientations of a cube with the specific conditions that the two unpainted faces are adjacent. If you organize your work well and follow a good model from beginning to end, solutions such as this are very attainable.
DPatrick (20:44:14)
OK, I'm going to turn things back over to Mathew Crawford, who will take you the rest of the way.
MCrawford (20:44:26)
Let's take a look at problem 10.
MCrawford (20:44:35)

MCrawford (20:44:43)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-215713278.gif
MCrawford (20:44:53)
Where can we start with this problem?
Bassooner_2 (20:44:51)
Dra a diagram
frodo (20:44:52)
Draw a coordinate plane.
MCrawford (20:45:07)
We don't really need a diagram for this one.
kops723 (20:45:04)
midpoint of BC
snare27 (20:45:25)
Find the equation the line with slope -5 that intersects the midpoint of BC
mna851 (20:45:26)
We can find the equation of the median
MCrawford (20:45:44)
We can begin by determining the line on which the median to BC lies.
Mr.Ocax (20:45:35)
we know that the line equation is y=-5+107
MCrawford (20:46:10)
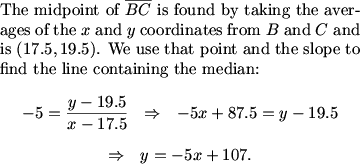
origamimasterjared (20:46:10)
And the equation of the median (y=-5x+107)
ginasboys (20:45:47)
Do we want to translate the triangle? (like we did in class)
MCrawford (20:46:33)
We could do that, but it's not necessary.
MCrawford (20:46:44)
Where can we go from here?
Zyloch_2 (20:45:15)
u can find area with determinants
joml88 (20:45:45)
Express area in terms of the determinant of a matrix and use the slope formula to set up a system of equations.
justdudxit (20:45:57)
Use a matrix method to equate p and q with a number
kops723 (20:46:47)
from here there will be 2 answers
MCrawford (20:47:17)
We are trying to find the values of x such that the triangle with coordinates (12, 19), (23, 20), and (x, -5x + 107) has area 70.
We could at this point resort to hunting down the nasty form of the distance from (x, -5x + 107) to the line containing B and C and using that as the height of the triangle, but there is a method for finding the areas of triangles that saves us a lot of trouble.
Sly Si (20:47:04)
Pick's Theorem give the area as a linear function of p and q!
MCrawford (20:47:32)
Pick's assumes lattice points.
lotrfan (20:47:32)
cross products give areas, and this method can be generalized using determinants.
mna851 (20:47:46)
Or Heron's theorem but that might get extremely messy.
MCrawford (20:48:05)
The area of a triangle is half of the absolute value of the determinant of the 3 x 3 matrix whose first column contains the values of the x-coordinates of the triangle, second column contains the values of the y-coordinates, and third column contains only 1's.
dts (20:45:42)
Use the formula: |determinant(p,q,1;12,19,1;23,20,1)|=area of triangle=1.
MCrawford (20:48:20)
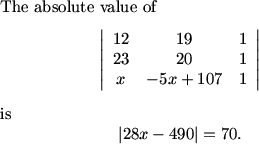
Bassooner_2 (20:48:16)
but if the answer asks us to add p and q and come up with an integers, aren't p and q both lattice points?
MCrawford (20:48:53)
Because the sum of two numbers is an integer does not mean they are both integers.
MCrawford (20:49:02)
However...
lotrfan (20:48:58)
don't we need to take one half of the determinant?
MCrawford (20:50:00)
Yes, sorry, forgot that.
MCrawford (20:50:14)
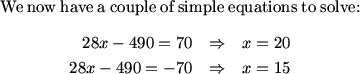
MCrawford (20:50:29)
What is our final answer?
fubu (20:47:47)
i used the matrix equation for using coordinates to find the area and got 11q-p=337. Then I used the midpoint of BC(35/2, 39/2) and pq to find a relationship for the -5 slope. i got 5p+q=107. so then q=32 and p=15. answer=47
Mr.Ocax (20:50:29)
we want 15
frodo (20:50:40)
107-15*4=47
fubu (20:50:50)
find the x that will maximize!
justdudxit (20:50:59)
20 is out of range
MCrawford (20:51:17)
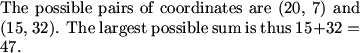
MCrawford (20:51:20)
We could also have noted that we needed only the smaller value of x as the sum of x and -5x + 107 is -4x + 107 which is a decreasing function. This means we're looking for the smaller value of x.
Bassooner_2 (20:50:33)
What was your however?
MCrawford (20:51:42)
I was thinking about whether we could imply from y = -5x + 107 and x + y = n that x and y are integers.
MCrawford (20:51:46)
Can we?
justdudxit (20:52:12)
no
Myself (20:52:18)
no. x = 1.5
pilot (20:52:19)
No
pika (20:52:30)
-4x+107=n
vfiroiu (20:49:58)
How would u solve this problem without a matrix?
joml88 (20:51:29)
Are there any 'nice' solutions without a matrix.?..it seems a little unlike them to require knowledge of a matrix to solve an AIME problem...
Geoffrey (20:53:05)
can we multiply all coordinates by four and use pick's? :-)
MCrawford (20:53:30)
Nice work Geoffrey!
MCrawford (20:53:37)
That's one possibility.
Mr.Ocax (20:53:47)
why multiply by 4?
MCrawford (20:54:03)
So that all the coordinates are necessarily integers.
justdudxit (20:53:56)
There's a sleight-of-hand trick you can use without a matrix. Hang on.
Bictor717 (20:47:38)
find the length of the height and use distance from point to line
MCrawford (20:54:34)
That's going to be a grind, but certainly possible.
Geoffrey (20:54:29)
because y+5x is integer, and x+y is integer, 4x and thus 4y are integers
origamimasterjared (20:54:16)
Wouldn't Pick's take too long?
MCrawford (20:55:06)
That depends on what kinds of calculations you are good at performing quickly.
origamimasterjared (20:54:49)
And it would be dangerous, because you could easily miscount.
Bassooner_2 (20:54:56)
we have 3 hours
kops723 (20:54:43)
you can use the shoelace theorem (don't know its oficialy name) where you line up all the coordinates vertically and then cross multiply by kind of drawing in a shoelace
Myself (20:55:17)
how do we find internal points?
MCrawford (20:55:33)
Inequalities.
kops723 (20:55:20)
what exactly is picks ive never heard of it
MCrawford (20:55:51)
We don't have time for a full discussion. Best to ask further on the message board.
DPopov (20:55:40)
I would recommend the shoelace
DPopov (20:55:44)
it worked nicely
DPopov (20:55:54)
since you have y in terms of x
Zratonx (20:56:00)
that is based on matrix...the ""the shoelace theorem""
MCrawford (20:56:17)
Let's move on to problem 11.
Mr.Ocax (20:56:14)
someone please post shoelace on the board too!!
MCrawford (20:56:31)
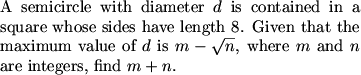
MCrawford (20:56:41)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-87568638.gif
MCrawford (20:56:47)
Without even jumping to a diagram, what can say about the relationship between the semicircle and the square?
mna851 (20:57:06)
They are tangent
pilot (20:57:08)
Tangent
Bictor717 (20:57:08)
semicircle is inscribed
MCrawford (20:57:26)
Actually, that's not trivial to prove.
MCrawford (20:57:41)
Many students got away with making this assumption however.
kops723 (20:57:46)
but it has to be otherwise it could be enlarged
MCrawford (20:58:12)
That's not yet clear and I've seen geometry problems where such an intuitive idea was false.
vfiroiu (20:58:07)
y prove it if u got 3 hours?
MCrawford (20:58:31)
You don't need to on the AIME of course, but that's why I personally thought this problem was a mistake.
MCrawford (20:58:47)
We know that the two endpoints of the semicircle will lie on sides of the square. If not, we could clearly expand the semicircle until they did hit sides.
MCrawford (20:58:49)

MCrawford (20:59:14)
Many of you want to jump to the conclusion that the diagram is symmetric and that the semicircle touches the square on all four sides (including the endpoints).
MCrawford (20:59:33)
The fact is that the largest semicircle does hit the square on all four sides, but it's not exactly obvious as to why this is true. I don't think the AIME committee intended for this step to be so obvious and for this reason this probably shouldn't have been a number 11.
MCrawford (20:59:41)
What can we do that would help us examine the orientation of the semicircle?
kops723 (21:00:02)
make it a full circle
MCrawford (21:00:33)
That might help you notice what's coming next.
vfiroiu (21:00:24)
bottom left triangle isosceles and right
MCrawford (21:00:46)
We don't yet know it's isosceles.
vfiroiu (21:00:31)
hypotenuse=diameter
frodo (21:00:49)
The median of the right triangle equal the radius of the circle.
MCrawford (21:01:15)
It makes sense to identify the center of the semicircle (the center of the full circle). This will allow us to begin making comparisons to the radius:
MCrawford (21:01:20)

MCrawford (21:01:27)

MCrawford (21:01:34)
The median from D in right triangle EFD must be half the hypotenuse and is therefore equal to r.
Bictor717 (21:00:19)
draw the radii to the sides of the square
MCrawford (21:01:48)
But we don't yet know that both radii will touch the square!
kostya_4 (21:01:37)
isn't the circle symmetrycal along the bottomleft to top right side...
MCrawford (21:02:14)
That's what we're trying to determine. Nobody has given a reason yet why this is true.
MCrawford (21:02:45)
Now, how can we compare the radius to the side of the square?
rachel (21:03:16)
r+rrt2/2=8
MCrawford (21:03:40)
Still based on assumptions... and nobody has given a reason for those assumptions.
DPopov (21:03:52)
What do we need to prove?
MCrawford (21:04:14)
That the semicircle is inscribed.
MCrawford (21:04:27)
There are many maximal area problems in which the figure cannot be inscribed.
MCrawford (21:05:10)

Someone (21:05:19)
Why not prove that the four points where the circle ""touches"" the square are cyclic?
MCrawford (21:05:43)
Because we haven't proved that the semicircle touches the square at four points.
MCrawford (21:05:49)
Those of you planning taking the USAMO -- beware!
MCrawford (21:06:12)
If you make these kinds of assumptions you'll find 0's on problems you would swear you got a 7 on.
beta (21:05:59)
the semicircle must touch at least 3 sides, or we could expand it
MCrawford (21:06:21)
That is true.
kops723 (21:05:49)
sin(X) = ON/r
MCrawford (21:06:44)
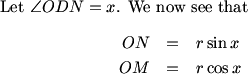
MCrawford (21:07:06)
How does this help us?
Sly Si (21:06:59)
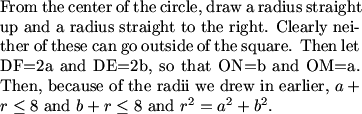
MCrawford (21:07:31)

MCrawford (21:07:42)
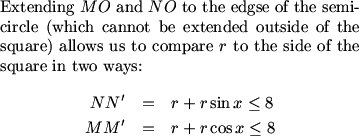
vfiroiu (21:07:58)
so this problem isn't ""proveable"" without trig?
MCrawford (21:08:33)
Myself has an idea that I'll drop in later that doesn't involve trig.
rachel (21:08:10)
MNOD is a square, so x=45
MCrawford (21:08:58)
We don't know that yet. It's only a rectangle by our assumptions.
dts (21:08:41)
Equality must hold for one of those, doesn't it?
MCrawford (21:09:14)
This we know!
MCrawford (21:09:18)
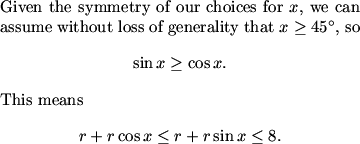
MCrawford (21:09:34)
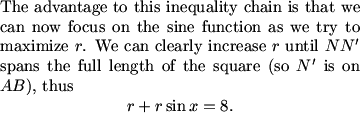
dts (21:09:21)
That is, it holds for the larger one.
dts (21:09:27)
It holds for both iff x=45.
MCrawford (21:10:03)
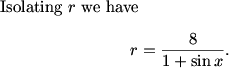
MCrawford (21:10:27)
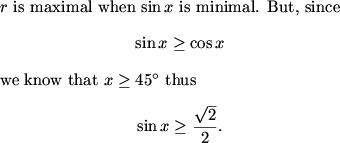
MCrawford (21:10:39)
We have now finally proved what many students got away with assuming -- namely that the figure is symmetric.
MCrawford (21:10:43)
What is our final answer?
DPopov (21:11:14)
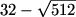
DPopov (21:11:00)
544
vfiroiu (21:11:08)
544
pika (21:11:25)
8/(1+1/sqrt2))=x
8/((sqrt2+1)/sqrt2)=x
MCrawford (21:11:35)
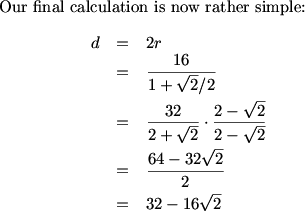
pika (21:11:32)
544
MCrawford (21:11:43)
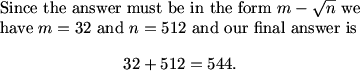
Sly Si (21:11:47)
Don't forget (as I did) that we're not actually looking for r.
MCrawford (21:12:13)
Myself has non-trig proof for the inscribing of the semicircle.
Myself (21:03:37)
AB is tangent to the circle. Let the contact point be D and the center of the circle be O. Then OD is perpendicular to AB because AB is tangent to the circle
Myself (21:06:15)
Let E vary on AD, but let DF = DE. When E is at D, the semicircle is smaller than the square. When E is at A, the semicircle is outside the square. At some point, the semicircle must go from inside to outside; this is the tangent point
MCrawford (21:13:05)
If you can think up this kind of argument, it's rigorous.
MCrawford (21:13:08)
Just be wary of assumptions without reasoning on the USAMO.
MCrawford (21:13:40)
Last year many students thought they got number 3 and got a 0 or a small number for that problem due to false or unproven assumptions.
vfiroiu (21:13:31)
this was alot easier than some of the previous ones
MCrawford (21:14:07)
Yes, but mostly because the intuitive fact that we proved was obvious. That's rare for a USAMO problem.
MCrawford (21:14:17)
On to problem 12.
MCrawford (21:14:26)
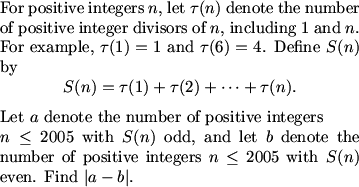
MCrawford (21:14:37)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-12794638.gif
MCrawford (21:14:43)
What do we know that is going to help us with this problem?
frodo (21:14:43)
There is an odd number of factors in squares.
peter (21:14:45)
only perfect squares have odd number of divisors
MCrawford (21:14:54)
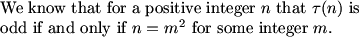
Mr.Ocax (21:14:51)
you know that s changes at perfect squares
fubu (21:14:54)
we know that since the number of factors of a square of a prime is odd, that is when the odd /even pattern changes
Myself (21:14:57)
we need to figure out when S(n) switches parity
MCrawford (21:15:07)
If this fact is new to you, I would suggest trying to prove it on your own. We cover two proofs of this in the AoPS Introduction to Number Theory class.
MCrawford (21:15:26)

Sly Si (21:15:19)
Thus, if you take the sequence S(1), S(2)... it switches parity at perfect squares.
kops723 (21:15:22)
we also know that the difference between two consecutive perfect squares is an odd number
MCrawford (21:15:43)
It we did not see this already, we discover that the parity (modulo 2 residue) of S(n) depends only on the number of perfect squares from 1 to n inclusive.
kops723 (21:15:39)
the difference between the next 2 consecutive squares is the next odd number
MCrawford (21:15:58)
We can now count the number of S(n) that are both even and odd by groups:
S(1) through S(3) are odd.
S(4) through S(8) are even.
S(9) through S(15) are odd.
S(16) through S(24) are even.
S(25) through S(35) are odd.
etc.
rachel (21:15:54)
5+9+...
Myself (21:15:55)
Notice that (n+1)^2 - (n^2) = n + n+1
Geoffrey (21:16:03)
we've got a sequence of 3 odd, 5 even, 7 odd, etc.
MCrawford (21:16:20)
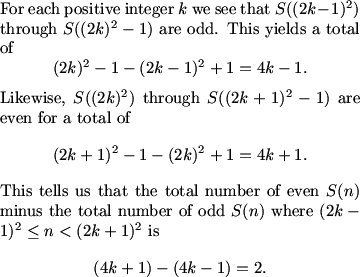
MCrawford (21:16:54)
What is the best way to break up these counts overall?
frodo (21:15:08)
44^2<2005<45^2
kops723 (21:17:23)
for every 2 switches of parity, the positive difference increases by 2 in favor of evenness
MCrawford (21:17:38)
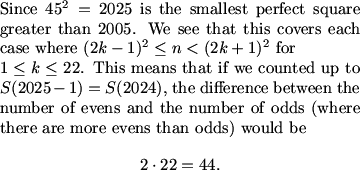
MCrawford (21:17:47)
How do we adjust for our final answer?
Geoffrey (21:17:47)
find out what floor(sqrt(2005)) is, and start with 2 * that, and then take care of everything from (that)^2 up to 2005.
MCrawford (21:18:07)
I went down from 2025, but either is fine.
Mr.Ocax (21:18:05)
you subtract 45^2-2005
MCrawford (21:18:16)
Close.
conartist (21:18:25)
add 1?
Mr.Ocax (21:18:34)
ack!!! my mistake!!!!nooooo
Geoffrey (21:18:52)
2024 -> 44, so 1908+x -> x. 2005 -> 25.
MCrawford (21:19:17)
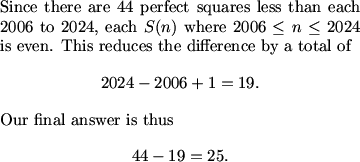
MCrawford (21:19:39)
There was no one exceedingly difficult step to this problem. However, there were a lot of little things that made it easier. First and foremost, recognizing that there was no need to count the divisors of any integers made the problem approachable. From there, expressing everything in modulo 2 make calculations much easier. The rest of the problem involved reasoning that, if kept organized, was not all that difficult.
MCrawford (21:20:03)
I personally liked the next problem:
MCrawford (21:20:08)

MCrawford (21:20:14)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-151992927.gif
MCrawford (21:20:21)
How might we attack such a problem?
Mr.Ocax (21:20:29)
the no right angle turns makes it much more difficult
dts (21:20:30)
Grind it out!
vfiroiu (21:20:35)
3 possible 1st steps?
alan (21:20:35)
brute force
Blaise (21:20:36)
Draw a diagram.
kops723 (21:20:42)
my coach had a good way--split up the total number of ways into an ordered triple, number of ways coming from below, from left, and from diagonal
MCrawford (21:21:03)
Numerous possible counting methods come to mind when thinking about this problem, though there doesn't seem to be any nice combinatoric approach.
MCrawford (21:21:08)
Sometimes simpler problems can help us get a grip on how we might solve the problem at hand. Sometimes we notice patterns or the essence of the problem.
conartist (21:21:09)
draw a tree, a very big tree [img id=em-3]
MCrawford (21:21:20)
There is only 1 way to get to (1, 1) without a right angle is to go straight there.
MCrawford (21:21:27)
There are 3 ways to go from (0, 0) to (2, 2). We can go through (1, 1), (1, 0), or (0, 1) with one set path from each of those points.
MCrawford (21:21:35)
The number of ways to get to (3, 3) and then (4, 4) looks like it's going to get difficult to count in a simple way rather quickly.
gibsnson (21:21:20)
define it recursively!
MCrawford (21:21:50)
That's what we'll do essentially.
Geoffrey (21:22:08)
it's hard to recurse, because sometimes you come in from a straight line, and you can't turn
MCrawford (21:22:26)
We'll get around that fact.
MCrawford (21:22:32)
We'll have to dig a little deeper into how this counting sequence is defined.
MCrawford (21:22:36)
Perhaps a picture would help:
MCrawford (21:22:39)

MCrawford (21:22:52)
The lower left hand corner is the origin and the upper right hand corner is (5, 5). Here we see the numbers of ways to get to each (1, 0), (1, 1), and (0, 1).
MCrawford (21:23:16)
Let us continue to draw upward paths in pink, diagonal paths in green, and horizontal paths in yellow, but we'll only draw the paths that take us to (2, 2) through some route.
MCrawford (21:23:35)

MCrawford (21:23:44)
It would have been nice if we could have done some simple block-walking labeling here, but the problem is that not all paths that lead from home to each point get counted.
MCrawford (21:24:03)
Given that the algorithm from where we can move each time is defined according to the last move, it makes sense to break the counts down into groups according to which direction the last path was walked:
MCrawford (21:24:10)

MCrawford (21:24:29)
Here the first number in each triplet describes the number of paths such that the last move was horizontal. The second number describes the number of paths such that the last move was diagonal. The third number describes the number of paths such that the last move was vertical.
kops723 (21:24:23)
thats what my coach did!
MCrawford (21:24:44)
According to the given algorithm, each first triplet entry will be the sum of the first two entries from the point immediately to the left. The second triplet entry will be the sum of all three entries from the point to the lower left. The third triplet entry will be the sum of the last two entries from the point immediately below.
MCrawford (21:25:02)
In this way we can now fill in the rest of the diagram with triplets (very carefully):
MCrawford (21:25:04)

MCrawford (21:25:12)
Adding up the entries at (5, 5) we get 28 + 27 + 28 = 83, our final answer.
MCrawford (21:25:30)
In order to solve this problem we needed to break out counting down in the way that the algorithm broke down the possible routes. Making this leap is essential to understanding how to work with algorithms and recursions (note that breaking the counts into three recursive groups would have been the same as the solution we walked through here).
frodo (21:25:26)
Cool.
MCrawford (21:25:43)
Here is a piece of advice I have on the modern AIME...
MCrawford (21:25:55)
When you get to problem 13 and beyond...
MCrawford (21:26:05)
Don't assume that there is a solution that avoids some grind.
Myself (21:26:01)
There is another way, breaking up the paths by the number of diagonal steps that they have
MCrawford (21:26:37)
There is a casework solution, but it's even uglier and doesn't generalize well.
MCrawford (21:26:52)
Now, let's take a look at 14.
MCrawford (21:27:00)

MCrawford (21:27:05)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-81731438.gif
MCrawford (21:27:10)
How should be begin?
conartist (21:27:19)
i actually tried using graph paper and measuring it out
Mr.Ocax (21:27:21)
draw a diagram
MithsApprentice (21:27:35)
You'll probably need a diagram here. Might as well connect ABCD
peter (21:27:46)
draw a diagram
MCrawford (21:28:01)
Let's start with an accurate picture
MCrawford (21:28:03)

MCrawford (21:28:07)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classes/AIME/Images/2005aime1_14_a.gif
MCrawford (21:28:12)
(The pictures for this problem are rather large, so you may want to click on the link to open them in a separate window.)
MCrawford (21:28:28)
What can we observe right away?
Mr.Ocax (21:29:02)
the square is going to be tilted?
Myself (21:29:34)
A and C are on opposite sides; B and D are on opposite sides
MCrawford (21:29:43)
We can see that since AC and BD intersected, the sides containing A and C are parallel, and the same for the sides containing B and D.
pika (21:29:41)
The square cannot have sides parallel to the axes
MCrawford (21:30:02)
How can we find the side length of the desired square?
frodo (21:30:06)
Are the points of the square integral?
MCrawford (21:30:26)
We don't know yet.
Myself (21:30:33)
I think we want to see how much it is rotated by, first
Myself (21:30:55)
I guess we can let the slope of the side containing A be m
MCrawford (21:31:06)
Suppose that the sides containing points A and C have slope m (where m is a positive real number).
This implies that the sides containing points B and D have slope -1/m, since they're perpendicular.
MCrawford (21:31:28)
Let's draw lines of slope m and -1/m through the origin:
MCrawford (21:31:32)

MCrawford (21:31:36)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classes/AIME/Images/2005aime1_14_b.gif
dts (21:30:41)
What I tried was drawing semicircles with radii AB, BC, CD, DA, so that each semicircle sticks out from the middle of ABCD, and each vertex must be on one of the semicircles... didn't get very far, though.
winluo2 (21:31:20)
Maybe draw semicircles with the sides as diameters, since there are right angles.
MCrawford (21:32:04)
There is such a solution involving finding the center of the square. I'll leave that up to discussion on the Message Board.
MCrawford (21:32:15)
Back to our diagram...
MCrawford (21:32:21)
What can we conclude?
aerlinndan (21:32:46)
question: did we just pick an arbitrary m to draw that last diagram?
MCrawford (21:33:13)
Essentially, though our drawing contains an assumption that we'll take care of later...
Myself (21:32:57)
we can find the equations of the lines passing through each side, then see if two sides have the same length
MCrawford (21:33:29)
We can conclude that the length of the side through B (or D) is the distance from A to the line of slope m plus the distance from C to the line of slope m.
Similarly the length of the side through A (or C) is the distance from B to the line of slope -1/m plus the distance from D to the line of slope -1/m.
MCrawford (21:33:33)
We may see this more clearly in the following picture:
MCrawford (21:33:39)

MCrawford (21:33:46)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classes/AIME/Images/2005aime1_14_c.gif
MCrawford (21:33:57)
(Note that we're making some assumptions here: we're assuming that the sides of the square through A and C have positive slope, and that the line of slope m through the origin passes through the square. But when we're done, we'll see that these assumptions are correct.)
MCrawford (21:34:02)
What are the distances from the points A,B,C,D to the respective lines?
Myself (21:34:37)
I wish I knew the formula.... but it would just be a simple application of whatever formlua it is
MCrawford (21:35:10)
The formula for the distance to a line with slope m is something you should learn to derive.
MCrawford (21:35:13)
It's very handy.
pika (21:35:06)
I think you'd need m first.
MCrawford (21:35:24)
We want this in terms of m.
fubu (21:35:21)
(Ax+By+c)/(sqrt(A^2+b^2))
MCrawford (21:35:39)
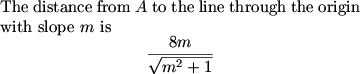
MCrawford (21:35:50)
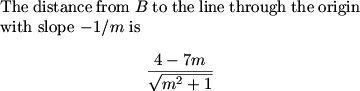
MCrawford (21:36:02)
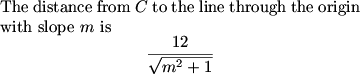
MCrawford (21:36:12)
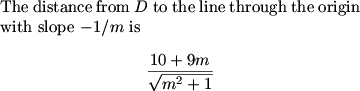
MCrawford (21:36:38)
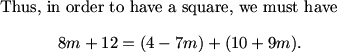
MCrawford (21:36:41)
So what is m?
gibsnson (21:37:01)
1/3
peter (21:37:08)
1/3
MCrawford (21:37:15)
We get that m=1/3.
What's the side of the square?
Bictor717 (21:38:41)
(12+8/3)/(sqrt(10/9))=44/sqrt10
MCrawford (21:38:47)
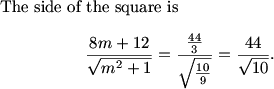
MCrawford (21:39:05)
So the area K of the square is 44^2/10, so 10K = 44^2 = 1936, hence the answer is 936.
MCrawford (21:39:14)
(Note: this solution is based on a solution due to Abhi Gulati, courtesy of AoPS user darktreb.)
MCrawford (21:39:45)
Those of you who know how to use complex numbers in geometry problems could also put this problem on a complex plane and make this solution a bit easier.
kops723 (21:39:48)
so is the comittee's solution uglier?
MCrawford (21:40:19)
It's nicer apparently, though I just heard about it and haven't had a chance to read it.
justdudxit (21:39:51)
Is there a way of using semicircles
MCrawford (21:40:34)
Yes, but carry that discussion to the Message Board.
MCrawford (21:40:45)
Now, let's take a look at the last problem!
MCrawford (21:40:47)

MCrawford (21:40:53)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Classroom/cbe6/images/lx-35480286.gif
MCrawford (21:41:00)
What is the most important first step in a tough AIME geometry problem?
pika (21:41:11)
DRAW A PICTURE?
MCrawford (21:41:18)
More specific!
Bictor717 (21:41:26)
accurate picture?
Myself (21:41:28)
draw an accurate picture
justdudxit (21:41:29)
Draw a good picture
aerlinndan (21:41:32)
draw a large, accurate picture
Geoffrey (21:41:34)
draw a clear picture where you can write stuff
MCrawford (21:41:48)
We draw the diagram large and as accurately as possible, and label what we know. When I worked this problem for the first time, I was lazy and spent 5 minutes working with a cramped diagram. I then drew it right and had the solution nearly immediately, just because drawing it right made me think about how to draw the diagram, which made me see the solution.
vfiroiu (21:41:44)
label everything
MCrawford (21:42:07)
How do we start when trying to draw the diagram well?
fubu (21:42:37)
trying to get the circle to actual divide the median into three equal lengths..i had a hard time
snare27 (21:42:44)
start with the circle trisecting the line
kops723 (21:42:45)
actually, median first, and then the circle to divide it
MCrawford (21:43:19)
We start with the trisected median CM - from there we can make a rough circle and draw the sides of the triangle tangent to the rough circle. It may take a couple tries, but you should get a decent picture.
MCrawford (21:43:22)
We then do a little labeling - we don't know much, but we do have the midpoint and the trisected segment to work with, and we have this:
MCrawford (21:43:31)

MCrawford (21:43:41)
We want the area of the triangle - what could we find that would give us the area?
dts (21:43:48)
The sides.
kops723 (21:43:51)
height
MCrawford (21:44:05)
We could find the altitude from C, or we could find AC and BC.
Which of these looks more promising and why?
kops723 (21:44:29)
im going to change my mind and say sides--walkaround
snare27 (21:44:32)
find AC and AB, because you can form two triangles wth two equal sides
pika (21:44:44)
AC and BC, because we can try to get those thru <bisector Thrm
Bictor717 (21:44:00)
herons formula, based on the form of the answer they want
MCrawford (21:45:09)
We start off looking for AC and BC, because it seems more likely we'll be able to use our incircle to go after those than to get the altitude from C.
MCrawford (21:45:24)
We have CY = CX, AY = AZ, and BX = BZ, which might be useful.
What tool does this diagram just cry out to try?
justdudxit (21:45:46)
Power of a point
MCrawford (21:46:08)
We have lengths, we want other lengths, and we have tangents and secants. We should try power of a point.
What point should we focus on?
pika (21:46:17)
C?
Bictor717 (21:46:21)
C and M
MCrawford (21:46:36)
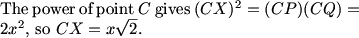
frodo (21:43:54)
Q is the centroid.
dts (21:43:57)
AC= 10, as well.
MCrawford (21:46:59)
What now?
MCrawford (21:47:27)
When we find something that works, the first thing we should do is try it again - maybe it will work again and give us more information.
MCrawford (21:47:35)
We go after the other end of our secant: point M. What do we find?
kostya_4 (21:47:11)
what is power of a point?
aerlinndan (21:47:39)
I'm off to the message boards to learn about what Power of a Point means...
MCrawford (21:48:03)
Yes, please take that discussion to the Message Board.
pika (21:48:02)
2x^2=ZM^2
MCrawford (21:48:14)
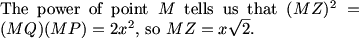
pika (21:47:27)
We have an isoceles
kops723 (21:47:27)
CY=CX
MCrawford (21:48:38)
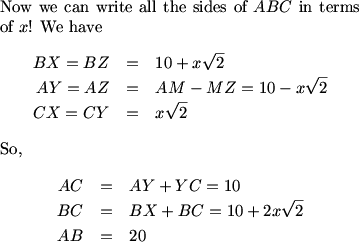
MCrawford (21:48:59)
We know we're close now. We have two of the sides of ABC and the third in terms of x.
What do we do?
pika (21:49:09)
Find x
MCrawford (21:49:24)
Sure, but we're going to need more information.
Bictor717 (21:49:18)
length of median formula, more generally Stewarts Thm
MCrawford (21:49:38)
At this point we may see our way to the solution - we have median CM in terms of x, we have AM = BM = 10, and we know AC and BC in terms of x, so we can just use Stewart to finish. Had we not thought of Stewart immediately, though, we might instead have tried to think of what fact we haven't made use of. This should lead us back to the midpoint (we've used AM and BM, but not the fact that they are equal). This might make us think of how to express the length of a median in terms of its sides.
MCrawford (21:49:58)
To find the length of a median in terms of its sides if we don't know Stewart's Theorem, consider the diagram again:
MCrawford (21:49:59)

pika (21:50:16)
cnc+bmb=dad+man
MCrawford (21:50:40)
If we continue CM to a point D such that ACBD is a parallelogram, what do we know about DM?
gibsnson (21:50:40)
Make it into a parallelogram
Myself (21:51:00)
DM = CM
Bictor717 (21:50:57)
DM=CM
MCrawford (21:51:35)
Which is...?
frodo (21:51:16)
""cynic bombed dads man"" is how I remember Steward's theorem
cczzzing (21:51:46)
3x\
Someone (21:51:47)
3x
kops723 (21:51:50)
3x
gibsnson (21:51:54)
3x
MCrawford (21:52:08)

MCrawford (21:52:16)
The diagonals of a parallelogram bisect each other, so DM = CM = 3x.
How does this help?
dts (21:51:59)
Ah. And the sum of the squares of the sides of a parallelogram is equal to the sum of the squares of the diagonals, so we can get CD directly, and thus get CM.
MCrawford (21:52:31)
The sum of the squares of the diagonals of a parallelogram equals the sum of the squares of the sides of the parallelogram.
In terms of the sides of ABC and median CM, what does this give us?
Mr.Ocax (21:53:23)
36*x^2+400=(10+2xsqrt2)^2+100
MCrawford (21:53:51)
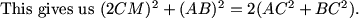
MCrawford (21:53:56)
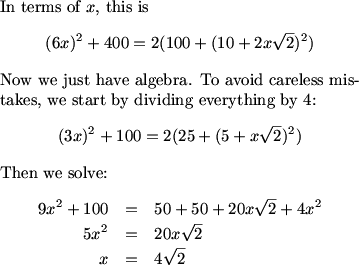
MCrawford (21:54:29)
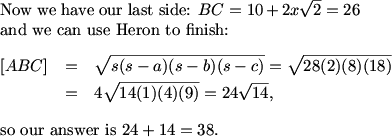
MCrawford (21:55:11)
There is a poll in the AMC for AIME scores.
gibsnson (21:55:02)
Wow, that was surprisingly doable.
MCrawford (21:55:33)
Yes, I think that was a little easier than average for a number 15.
dts (21:55:20)
Overall, what was your opinion on this AIME?
MCrawford (21:56:04)
Slightly on the easy side and there were too many problems with gimmicky math-team shortcuts or assumptions that could be made that made the problems easier.
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.









