Math Jams

copeland 2015-02-04 18:50:37
The Math Jam will start at 7:00 PM Eastern / 4:00 PM Pacific.

copeland 2015-02-04 18:50:39
The classroom is moderated, meaning that you can type into the classroom, but these comments will not go directly into the room.

copeland 2015-02-04 18:50:41
Please do not ask about administrative aspects of the contests, and please do not ask me to speculate about the results.

mathmaster2000 2015-02-04 18:52:10
Hello

stuff1014 2015-02-04 18:52:10
hi

Onomatopoeia 2015-02-04 18:52:10
hello

mathwrath 2015-02-04 18:52:10
Hello

SirCalcsALot 2015-02-04 18:52:10
Hello copeland

chococheese15 2015-02-04 18:52:10
hi

droid347 2015-02-04 18:52:10
Hello!

chococheese15 2015-02-04 18:52:10
hi

copeland 2015-02-04 18:52:11
Hi everybody.

masad24 2015-02-04 18:52:39
hi c:

dragonfly 2015-02-04 18:52:39
hi

bluehall90 2015-02-04 18:52:39
Hiii

SVstudent2013 2015-02-04 18:52:39
hi

PingThePanda 2015-02-04 18:52:39
hi

DeathLlama9 2015-02-04 18:52:39
Hi Mr. Copeland!

brian22 2015-02-04 18:52:39
Hi.

hesa57 2015-02-04 18:52:59
I cannot join right now; when can I see the transcript?

copeland 2015-02-04 18:53:01
The transcript will be available soon after the Math Jam.

droid347 2015-02-04 18:53:44
Mr. Copeland, did you think this AMC 10 was way more "troll" than other AMC 10s?

copeland 2015-02-04 18:53:45
Troll, huh? I saw the word "trolly" on the site and thought 'ding-ding!'

brian22 2015-02-04 18:54:07
soon after can range from a few hours to a few days

copeland 2015-02-04 18:54:08
By tomorrow morning, PT.

brian22 2015-02-04 18:54:29
lol it's spelled trolley I thiink

copeland 2015-02-04 18:54:33
Yeah. . .

SimonSun 2015-02-04 18:54:59
do you think they will make the achievement role requiment higher?

copeland 2015-02-04 18:55:00
I won't speculate on what the AMC will do with the scores.

xantho 2015-02-04 18:55:39
Do the moderators have any know-how of whats holding back the 10A answers?

copeland 2015-02-04 18:55:40
My theory is Problem 20.

ralph4imo 2015-02-04 18:56:10
Mr. Copeland, can we discuss problems outside the final five? (14 in particular)

copeland 2015-02-04 18:56:11
We will probably only discuss the last 5, with a note on a couple others.

IequalSmart 2015-02-04 18:56:52
I feel like we are the press, asking you all our questions. lol

copeland 2015-02-04 18:56:53
I feel like the President, or maybe Madonna.

1023ong 2015-02-04 18:57:08
what's the schedule for tonight? shared problems first or amc 10 first or what?

copeland 2015-02-04 18:57:10
I'll explain the schedule when we get started.

JOHNSUNG 2015-02-04 18:57:46
How long will the math jam last?

champion999 2015-02-04 18:57:46
How long will this Math Jam be?

copeland 2015-02-04 18:57:47
Probably around 3 hours.

TheMaskedMagician 2015-02-04 18:58:20
Will Mr. Rusczyk be making videos for the final 5 this year?

copeland 2015-02-04 18:58:22
Yes!

copeland 2015-02-04 18:58:30
I'll post a link at the end of the session.

mathawesomeness777 2015-02-04 18:59:05
Has MAA posted the AMC 10 Answers?

copeland 2015-02-04 18:59:06
They hadn't 20 minutes ago. I don't know when those will go up.

AoPSNovice314 2015-02-04 18:59:54
Just a fun question before the math jam starts, what is your favorite number Mr. Copeland?

copeland 2015-02-04 18:59:55
225.

liant 2015-02-04 19:00:26
why

imath2013 2015-02-04 19:00:26
why?

miloszeman 2015-02-04 19:00:26
Why?

zmyshatlp 2015-02-04 19:00:26
Why?

liant 2015-02-04 19:00:26
Why

gradysocool 2015-02-04 19:00:26
Why 225?

bharatputra 2015-02-04 19:00:26
why is it your favorite number

mango99 2015-02-04 19:00:26
why?

sarvottam 2015-02-04 19:00:26
15^2

myungsooglee 2015-02-04 19:00:26
why?

jrexmo 2015-02-04 19:00:26
Any reason?

5cmpersun 2015-02-04 19:00:26
why?

copeland 2015-02-04 19:00:32
Weird. I never thought about why. . .

DeathLlama9 2015-02-04 19:00:42
What is your least favorite number?

copeland 2015-02-04 19:00:43
3665.

copeland 2015-02-04 19:00:59
Should we get started?

Kiola 2015-02-04 19:01:16
Yessssss

atmchallenge 2015-02-04 19:01:16
yes

kwausouq 2015-02-04 19:01:16
Yea

RoboMan 2015-02-04 19:01:16
sure!

liant 2015-02-04 19:01:16
idk

goodbear 2015-02-04 19:01:16
yes.

copeland 2015-02-04 19:01:19
Welcome to the 2014 AMC 10A/12A Math Jam!

copeland 2015-02-04 19:01:20
I'm Jeremy Copeland, and I'll be leading our discussion tonight.

copeland 2015-02-04 19:01:23
I'm the school director here at AoPS. That means when something goes wrong, I either get yelled at or have to yell at someone else. Before AoPS, I was an instructor at MIT, and before that I got my Ph.D. from the University of Chicago. Before that I was an undergrad at Reed College and going back even further, I can't really remember. I used to have hobbies, but I'm a parent now, so those days are all over.

copeland 2015-02-04 19:01:33
Before we get started I would like to take a moment to explain our virtual classroom procedures to those who have not previously participated in a Math Jam or one of our online classes.

copeland 2015-02-04 19:01:36
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.

mathawesomeness777 2015-02-04 19:01:49
How do you type so fast?

copeland 2015-02-04 19:01:50
I have 2 keyboards.

copeland 2015-02-04 19:01:56
Moderation helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.

copeland 2015-02-04 19:02:00
There are a ton of students here! (Actually a lot closer to 50 tons, which is fewer tonnes, and only around 35 tuns.) As I said, only a fraction of the well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!

copeland 2015-02-04 19:02:11
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the prerequisite material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!

copeland 2015-02-04 19:02:29
We have 3 assistants tonight: Alina Kononov (laughinghead505), Benjamin Engwall (bluecarneal), and Jackie Brendenberg (3628800J).

copeland 2015-02-04 19:02:32
Alina joined AoPS in 2006 as a young, impressionable mathematician. She is an alumna of MathPath, Canada/USA Mathcamp, the Illinois Math and Science Academy, and MIT. Currently, she is a graduate student in physics at the University of Illinois at Urbana-Champaign. In her scraps of free time, Alina enjoys eating and making sweets, reading science fiction, crafting, and exploring urban areas.

copeland 2015-02-04 19:02:34
Benjamin is currently participating in Georgia Tech's Online Masters program for Computer Science - one of his favorite subjects. He has been an active member of the AoPS community since 2008, and thoroughly enjoys the opportunity he has to be a Grader and TA. In his spare time, he enjoys swimming competitively, reading, and pretending he can golf.

copeland 2015-02-04 19:02:43
Jackie lives in Michigan, where she won the statewide Michigan Math Prize Competition. She was also a 3-time USA(J)MO qualifier and a member of the USA team at the International Linguistics Olympiad. She plans to major in math and computer science. In her free time, she enjoys cooking, running cross country, and solving crossword puzzles.

laughinghead505 2015-02-04 19:02:54
Hi everyone!

bluecarneal 2015-02-04 19:02:57
Hello!

3628800J 2015-02-04 19:02:58
Hello!

ralph4imo 2015-02-04 19:03:23
Hello!

geogirl08 2015-02-04 19:03:23
hi

zew 2015-02-04 19:03:23
hi!

SimonSun 2015-02-04 19:03:23
hi!!!!!!!!!

math0127 2015-02-04 19:03:23
hi! thanks for being here!

winnertakeover 2015-02-04 19:03:23
hi

Art123 2015-02-04 19:03:23
Hi!

kunsun 2015-02-04 19:03:23
hi

zmyshatlp 2015-02-04 19:03:23
Hello!

copeland 2015-02-04 19:03:26
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the incredibly large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.

Bob_Smith 2015-02-04 19:03:37
what about v_Enhance?

copeland 2015-02-04 19:03:38
I see him! He's just here for fun I think.

copeland 2015-02-04 19:03:42
Please also remember that the purpose of this Math Jam is to work through the solutions to AMC problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be posted.

copeland 2015-02-04 19:03:47
Also notice that there will be several cases where we actually find the answer or almost the answer but instead wander off. The goal is always to find a proof that our answer is correct and not just find the answers. Of course on the AMC you should aim to do much less work than this.

copeland 2015-02-04 19:04:02
We will work the last 5 problems from the AMC 10A, then the last 5 problems from the AMC 12A. Two of these problems are the same, 10A Problem 25 and 12A Problem 23. We'll only solve that problem once.

copeland 2015-02-04 19:04:12
We usually promise to chat about other problems on the test, but honestly, I tend to meander and most of us will be exhausted by the end of these 9 problems.

copeland 2015-02-04 19:04:18
Let's get started!

thatindiankid10 2015-02-04 19:04:45
Yay!

stuff1014 2015-02-04 19:04:45
ok

jerryfu 2015-02-04 19:04:45
Lets a go!

hibiscus 2015-02-04 19:04:45
Yahoo!

prpaxson 2015-02-04 19:04:45
Yay!

katmcphie 2015-02-04 19:04:45
yay!

mishka1980 2015-02-04 19:04:45
Yay!

copeland 2015-02-04 19:04:52
Oh, and there truly are a lot of people here tonight. I really don't like saying it, but we're probably going to miss some of the things that some of you say. (Especially during the geometry problems - sheesh.) Please forgive me in advance. That doesn't happen in our classes.

copeland 2015-02-04 19:04:58
Let's start with the most interesting problem on the exam. This problem was on both exams:

copeland 2015-02-04 19:04:59
AMC 10 Problem 5/AMC12 Problem 3. Mr. Patrick teaches math to 15 students. He was grading tests and found that when he graded everyone's test except Payton's, the average grade for the class was 80. After he graded Payton's test, the class average became 81. What was Payton's score on the test?
$\phantom{peekaboo!}$
$\text{(A) } {81} \quad \text{(B) } {85} \quad \text{(C) } {91} \quad \text{(D) } {94} \quad \text{(E) } {95}$

flyrain 2015-02-04 19:05:32
it was e

yingzesen 2015-02-04 19:05:32
e

hibiscus 2015-02-04 19:05:32
E

ralph4imo 2015-02-04 19:05:32
95 E

Ultimate_draco 2015-02-04 19:05:32
E

yingzesen 2015-02-04 19:05:32
it s e

kevin2000 2015-02-04 19:05:32
95

Onomatopoeia 2015-02-04 19:05:32
E

profmath 2015-02-04 19:05:32
E

copeland 2015-02-04 19:05:43
We believe that this problem is in homage to our very own Dave Patrick. Dear AMC dudes, it should be Dr. Patrick.

copeland 2015-02-04 19:05:49
If Payton scores an 80 the average would still be 80. Instead Payton needs to make up 1 point for each student in the class so he needs to score a $80+15=95.$ The answer is (E).

copeland 2015-02-04 19:05:55
Now for reals. . .

copeland 2015-02-04 19:05:56
21. Tetrahedron $ABCD$ has $AB=5$, $AC =3$, $BC=4$, $BD=4$, $AD=3$, and $CD=\frac{12}{5}\sqrt{2}$. What is the volume of the tetrahedron?
$\phantom{peekaboo!}$
$\text{(A) } {3\sqrt{2}} \quad \text{(B) } {2\sqrt{5}} \quad \text{(C) } {\dfrac{24}{5}} \quad \text{(D) } {3\sqrt{3}} \quad \text{(E) } {\dfrac{24}{5}\sqrt{2}}$

copeland 2015-02-04 19:06:04
You might ask if there is an equivalent of Heron's Formula for a tetrahedron, where we can plug in the six sides and get the volume. It turns out there is, but it's incredibly complicated.

copeland 2015-02-04 19:06:05
http://en.wikipedia.org/wiki/Heron%27s_formula#Heron-type_formula_for_the_volume_of_a_tetrahedron

copeland 2015-02-04 19:06:17
Did anybody use that method?

shiningsunnyday 2015-02-04 19:06:29
I tried using Heron's formula on the test...

1491625E 2015-02-04 19:06:29
yes

xantho 2015-02-04 19:06:29
Yes!

jrexmo 2015-02-04 19:06:29
NO way

SVstudent2013 2015-02-04 19:06:29
Um... no

stan23456 2015-02-04 19:06:29
nooo

copeland 2015-02-04 19:06:36
What do you notice about the given numbers?

mathawesomeness777 2015-02-04 19:06:54
3 - 4 -5 trianglw

forthegreatergood 2015-02-04 19:06:54
Right triangles

droid347 2015-02-04 19:06:54
3-4-5 right triangles!

Bob_Smith 2015-02-04 19:06:54
3-4-5 triangle

ninjataco 2015-02-04 19:06:54
3-4-5 right triangle!

TheMaskedMagician 2015-02-04 19:06:54
3-4-5 right triangle

qwerty137 2015-02-04 19:06:54
3-4-5 right triangles

copeland 2015-02-04 19:07:02
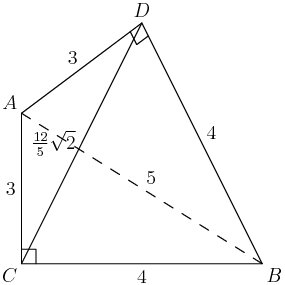
$ABC$ is a 3-4-5 right triangle!

copeland 2015-02-04 19:07:07
So is $ABD$!

copeland 2015-02-04 19:07:10
OK, now what?

copeland 2015-02-04 19:07:17

awesomethree 2015-02-04 19:07:42
Find the altitude

thiennguyen 2015-02-04 19:07:42
figure out the height

thetank 2015-02-04 19:07:42
find tha base area

DeathLlama9 2015-02-04 19:07:42
Find the height!

Studiosa 2015-02-04 19:07:42
Right angles, so area of base times height

blueberry7 2015-02-04 19:07:42
find the height

copeland 2015-02-04 19:07:51
The formula for the volume is $\frac13bh$, where $b$ is the area of a base, and $h$ is the height to that base.

copeland 2015-02-04 19:07:55
We can find base areas easily enough: $[ABC] = [ABD] = 6$ gives us two candidates for bases. What about heights?

copeland 2015-02-04 19:08:02
Let's draw in the two heights and see if that helps. How?

AlcumusGuy 2015-02-04 19:08:46
draw an altitude

pedronr 2015-02-04 19:08:46
Draw the altitudes of the right triangles

qwerty137 2015-02-04 19:08:46
altitudes from C and D to AB are 12/5

gradysocool 2015-02-04 19:08:46
Find the altitude of ADB connecting to AB?

swirlykick 2015-02-04 19:08:46
notice the altitude to hypotenuse of 3-4-5 triangle is 12/5

legozelda 2015-02-04 19:08:46
altitude of ABC and ABD from side length 5 make a right triangle(12.5)

awesomethree 2015-02-04 19:08:46
From D to AB

Blobbypie 2015-02-04 19:08:46
Draw heights to 345 triangles

copeland 2015-02-04 19:08:50
Well, we can start by drawing the altitudes on the bases first. That is, I'll draw the altitude from $C$ to $\overline{AB}$, and the altitude from $D$ to $\overline{AB}$.

copeland 2015-02-04 19:09:00
These go to the same point because the two faces $ABC$ and $ABD$ are congruent, the two altitudes will hit $\overline{AB}$ at the same point. Let's call it $X$.

copeland 2015-02-04 19:09:08

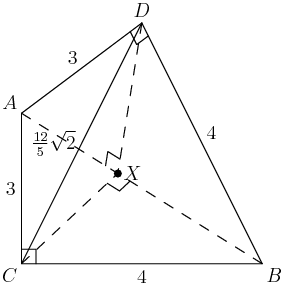
copeland 2015-02-04 19:09:27
What (if anything) do we know about $X$? $CX$? $DX$?

warrenwangtennis 2015-02-04 19:09:45
DX = 12/5!

Deathranger999 2015-02-04 19:09:45
The altitude will be 12/5.

pnpiano 2015-02-04 19:09:45
CX = 12/5 and Dx = 12/5 and both are heights

danusv 2015-02-04 19:09:45
DX^2+C^2=CD^2 because altitude of a 345 triangle is 12/5

ninjataco 2015-02-04 19:09:45
CX=DX=12/5

fluffyanimal 2015-02-04 19:09:45
XD=XC=12/5

spin8 2015-02-04 19:09:45
cx-12/5

copeland 2015-02-04 19:09:54
The area of $ABC$ is 6, so $\frac12(CX)(AB) = 6.$

copeland 2015-02-04 19:09:55
But $AB = 5$, so that means $CX = \frac{12}{5}.$

copeland 2015-02-04 19:09:58
Aha! There's already a $\frac{12}{5}$ in our diagram. That's probably not a coincidence!

copeland 2015-02-04 19:09:59
By symmetry, $DX = \frac{12}{5}$ too.

copeland 2015-02-04 19:10:00
So what does that tell us about triangle $CXD$?

mathwizard888 2015-02-04 19:10:29
isosceles right

WhaleVomit 2015-02-04 19:10:29
its a 45-45-90 triangle

champion999 2015-02-04 19:10:29
cxd is a 45 45 90 triangle

ExuberantGPACN 2015-02-04 19:10:29
45 45 90 right triangle!

GU35T-31415 2015-02-04 19:10:29
45-45-90 triangle

FlyingWombat 2015-02-04 19:10:29
45-45-90 triangle

liopoil 2015-02-04 19:10:29
it must be a 45-45-90 triangle

elpers21 2015-02-04 19:10:29
45 45 90 triangle

mjoshi 2015-02-04 19:10:29
isosceles right

copeland 2015-02-04 19:10:32
It's an isosceles right triangle! (The hypotenuse $CD$ is $\sqrt{2}$ times the equal legs $CX$ and $DX$.)

copeland 2015-02-04 19:10:34
So what?

6stars 2015-02-04 19:11:19
we have the height

andycai2000 2015-02-04 19:11:19
and, more importantly, it tells us that DX and CX are heights for the tetrahedron

MathCompetitor0606 2015-02-04 19:11:19
we can get the height now, which is 12/5

bookworm2003 2015-02-04 19:11:19
The height is also 12/5

Quadratic64 2015-02-04 19:11:19
DX is perpendicular to plane of ABC

5cmpersun 2015-02-04 19:11:19
12/5 is the height

pnpiano 2015-02-04 19:11:19
we have the height =12/5

CornSaltButter 2015-02-04 19:11:19
The altitude for our 3-4-5 (12/5) is also our height for the pyramid!

Kevin100 2015-02-04 19:11:19
so 12/5 is the altitude to our 3-4-5 base

copeland 2015-02-04 19:11:21
So, that means that $\overline{DX}$ is perpendicular to $\overline{CX}$.

copeland 2015-02-04 19:11:24
And since we already knew that $\overline{DX}$ is perpendicular to $\overline{AB}$ as well, we can conclude that $\overline{DX}$ is perpendicular to the plane containing $ABC$. That is, $\overline{DX}$ is the altitude from $D$ to the plane containing $ABC.$

copeland 2015-02-04 19:11:25
So $DX$ is the height to base $ABC$, and now we can compute the volume.

MathMaestro9 2015-02-04 19:11:58
It is 24/5 I think.

wehac 2015-02-04 19:11:58
the volume is 1/3*12/5*6=24/5

Wiggle Wam 2015-02-04 19:11:58
$6 \cdot 12/5 \cdot 1/3=\frac{24}{5}$

yayups 2015-02-04 19:11:58
C

yayups 2015-02-04 19:11:58
24/5

SimonSun 2015-02-04 19:11:58
(c) 24/5

imak64 2015-02-04 19:11:58
24/5

math0127 2015-02-04 19:11:58
6 * 12/5 / 3 = 24/5

copeland 2015-02-04 19:12:01
The volume is
\[
\frac13bh = \frac13(DX)[ABC] = \frac13 \cdot \frac{12}{5} \cdot 6 = \frac{24}{5}.
\]
Answer (C).

copeland 2015-02-04 19:12:05
Alright, good start.

copeland 2015-02-04 19:12:12
22. Eight people are sitting around a circular table, each holding a fair coin. All eight people flip their coins and those who flip heads stand while those who flip tails remain seated. What is the probability that no two adjacent people will stand?
$\phantom{peekaboo!}$
$\text{(A) } {\dfrac{47}{256}} \quad \text{(B) } {\dfrac{3}{16}} \quad \text{(C) } {\dfrac{49}{256}} \quad \text{(D) } {\dfrac{25}{128}} \quad \text{(E) } {\dfrac{51}{256}}$

copeland 2015-02-04 19:12:18
Probability problem. What's this smell like to you?

ompatel99 2015-02-04 19:12:59
Cases?

JoyAn 2015-02-04 19:12:59
casework

az_phx_brandon_jiang 2015-02-04 19:12:59
Casework

zmyshatlp 2015-02-04 19:12:59
casework!

mathwrath 2015-02-04 19:12:59
Casework

ralph4imo 2015-02-04 19:12:59
Casework!

copeland 2015-02-04 19:13:02
I'm getting a strong urge to try casework here.

copeland 2015-02-04 19:13:04
We have $2^8=256$ total ways to flip 8 coins. We need to count all the ways that the flips can come up such that no two heads are adjacent.

copeland 2015-02-04 19:13:05
What are the cases?

TheStrangeCharm 2015-02-04 19:13:42
0,1,2,3, or 4 heads

NeilOnnsu 2015-02-04 19:13:42
0, 1, 2, 3, or 4 heads

ryanyoo 2015-02-04 19:13:42
4 people standing, 3, 2, 1, none

cumo99 2015-02-04 19:13:42
0,1,2,3,4 people

bli1999 2015-02-04 19:13:42
0, 1, 2, 3, 4 heads

mathway 2015-02-04 19:13:42
0,1,2,3,4 people stand up

pedronr 2015-02-04 19:13:42
number of people who flip heads is 0,1,2,3,4

GeorgCantor 2015-02-04 19:13:42
1 person stands up, 2 people stand up, etc

kunsun 2015-02-04 19:13:42
0 standing, 1 standing, ... up to 4 standing

MathStudent2002 2015-02-04 19:13:42
0 people stand, 1 person stands, 2 people stand, 3 people stand, 4 people stand

copeland 2015-02-04 19:13:44
We can have 0, 1, 2, 3, or 4 heads. Any more and we would need to have two neighbors come up heads.

copeland 2015-02-04 19:13:47
So it's a constructive casework problem. I find these really soothing when I don't have anything else to do and there is no need to rush. . .

copeland 2015-02-04 19:13:51
How many ways can we flip 0 heads?

lucylai 2015-02-04 19:14:12
1

yayups 2015-02-04 19:14:12
1

mjlove 2015-02-04 19:14:12
1 way

Gina 2015-02-04 19:14:12
1 way

RoboMan 2015-02-04 19:14:12
1

kungfugirl 2015-02-04 19:14:12
1

Elaine09 2015-02-04 19:14:12
1

jeremylu 2015-02-04 19:14:12
1

prpaxson 2015-02-04 19:14:12
1

copeland 2015-02-04 19:14:15
Just 1. Everyone flips tails.

copeland 2015-02-04 19:14:17
How many ways can we flip 1 heads?

mattlim 2015-02-04 19:14:44
There are 8 ways to flip one head

gradysocool 2015-02-04 19:14:44
8

JoyAn 2015-02-04 19:14:44
8

blueberry7 2015-02-04 19:14:44
8

Annabeth 2015-02-04 19:14:44
8 ways

coolcandii 2015-02-04 19:14:44
8

DeathLlama9 2015-02-04 19:14:44
8

Elaine09 2015-02-04 19:14:44
8

Jwilson1990J 2015-02-04 19:14:44
8

vimathur 2015-02-04 19:14:44
8

shakeNbake 2015-02-04 19:14:44
8

copeland 2015-02-04 19:14:47
There are 8 choices for who flips heads and since there is only one, there can't be two next to each other.

copeland 2015-02-04 19:14:54
Let's look at flipping 2 heads. What should we do?

geogirl08 2015-02-04 19:15:42
complementary

mishka1980 2015-02-04 19:15:42
We do $\binom{8}{2}-8$

GU35T-31415 2015-02-04 19:15:42
Count total and subtract the consecutive pairs

ryanyoo 2015-02-04 19:15:42
8C2 - 8 = pick any two spots, subtract adjacent cases

yuunderstand168 2015-02-04 19:15:42
8 choose 2 - 8

DeathLlama9 2015-02-04 19:15:42
8c2 - (number of ways for them to be next to each other)

donot 2015-02-04 19:15:42
$\binom{8}{2}$ (ways to flip 2 heads) minus $8$ (number of pairs)=$20$?

copeland 2015-02-04 19:15:44
We could say that there are $\binom82=28$ different ways to flip 2 heads and 8 of those are bad (there are 8 pairs of neighbors and each pair is determined by its leftmost member). That gives 20.

warrenwangtennis 2015-02-04 19:16:16
8 choices for first one, 5 ways for second, but divide by 2!

CombatOmega 2015-02-04 19:16:16
8 * 5, instead of 8 * 7, because it can't be the people next to the first

hjl00 2015-02-04 19:16:16
8 * 5 / 2 = 20

MathCompetitor0606 2015-02-04 19:16:16
8 times 5 seats.. since they can't be adjacent

copeland 2015-02-04 19:16:18
Alternatively, we could pick one of the 8 to be heads and that leaves 5 others who could also be heads. But. . .

copeland 2015-02-04 19:16:22
that overcounts by a factor of 2 since we could pick in either order. This gives $\dfrac{8\cdot5}2=20$ again.

copeland 2015-02-04 19:16:25
What about three heads? Theories for how to count that?

legozelda 2015-02-04 19:17:07
for 3 use casework where for the bad outcomes, either 3 in a row or 2 and 1 away

fractal161 2015-02-04 19:17:07
Sub-casework?

ninjataco 2015-02-04 19:17:07
complementary again

Kevin100 2015-02-04 19:17:07
there are 2 further cases - sitting 2 away or 3/4 away from the first guy

geogirl08 2015-02-04 19:17:07
complements again?

copeland 2015-02-04 19:17:11
We can place three heads in $\binom83=56$ ways. That counts 8 bad ways to put all three together. That also counts the bad ways to put two together with another singleton.

copeland 2015-02-04 19:17:13
How many ways can you place 2 heads together and then another singleton?

DeathLlama9 2015-02-04 19:17:36
Singleton?

blueduck1 2015-02-04 19:17:36
What is a singleton

copeland 2015-02-04 19:17:38
One by himself.

swirlykick 2015-02-04 19:17:53
8*4=32

sl_huskies 2015-02-04 19:17:53
8*4=32

CornSaltButter 2015-02-04 19:17:53
8*4=32

ExuberantGPACN 2015-02-04 19:17:53
8 x 4 = 32

fluffyanimal 2015-02-04 19:17:53
8x4=32

alex31415 2015-02-04 19:17:53
8x4=32

BFYSharks 2015-02-04 19:17:53
4*8?

Abecissa 2015-02-04 19:17:53
8*4=32

copeland 2015-02-04 19:17:55
There are 8 places for the singleton and then the pair needs to be among the other 5. There are 4 neighboring pairs so there are $8\cdot4=32$ total bad flips with a pair and a singleton.

copeland 2015-02-04 19:17:56
There are $56-8-32=16$ total successful 3-head flips.

copeland 2015-02-04 19:18:01
Or we could also just try placing all the heads. They must be configured like this:

copeland 2015-02-04 19:18:05

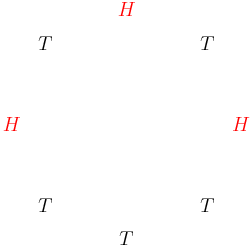
copeland 2015-02-04 19:18:09

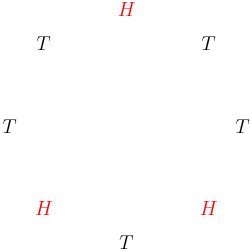
copeland 2015-02-04 19:18:12
There are 8 distinct ways to rotate each of these so 16 total successful 3-head flips.

copeland 2015-02-04 19:18:16
What about 4 heads?

andycai2000 2015-02-04 19:18:42
2

awesomethree 2015-02-04 19:18:42
2, cause odd or even

droid347 2015-02-04 19:18:42
2 ways?

1491625E 2015-02-04 19:18:42
2

kwausouq 2015-02-04 19:18:42
2 ways

ericding 2015-02-04 19:18:42
2

danusv 2015-02-04 19:18:42
2 ways

briyellowduck 2015-02-04 19:18:42
2

copeland 2015-02-04 19:18:44
There are only 2 4-head successes:

copeland 2015-02-04 19:18:46

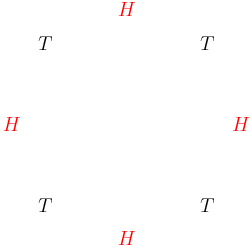
copeland 2015-02-04 19:18:48

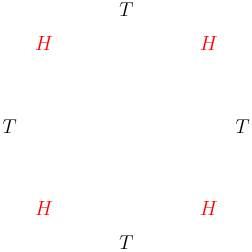
copeland 2015-02-04 19:18:49
So the answer?

Seasend 2015-02-04 19:19:32
47/256

SimonSun 2015-02-04 19:19:32
(C)

eswa2000 2015-02-04 19:19:32
A

math_cool 2015-02-04 19:19:32
47/256 = A

pfalcon607133 2015-02-04 19:19:32
A

subhasri 2015-02-04 19:19:32
2

MathematicsOfPi 2015-02-04 19:19:32
$\frac{47}{256}$

Jayjayliu 2015-02-04 19:19:32
47

yimingz89 2015-02-04 19:19:32
47/256 a)

jfei2001 2015-02-04 19:19:32
47/256

bomb427006 2015-02-04 19:19:32
47/256 (A)

MathMaestro9 2015-02-04 19:19:32
so it is 47/256

GeorgCantor 2015-02-04 19:19:32
1 + 8 + 20 + 32 + 2

wcao9311 2015-02-04 19:19:32
A 47/256

copeland 2015-02-04 19:19:35
We divide by the total number of options to get a probability: \[\frac{1+8+20+16+2}{256}=\boxed{\dfrac{47}{256}}.\] The answer is A.

copeland 2015-02-04 19:19:46
Alright, cool. Now we're rocking.

Deathranger999 2015-02-04 19:19:54
Is there a way to do that without casework?

copeland 2015-02-04 19:19:56
Yes.

copeland 2015-02-04 19:20:12
If you make every heads have a tails following it, then all the heads come in 2-person bricks.

copeland 2015-02-04 19:20:19
HT

copeland 2015-02-04 19:20:22
Or you could just drop an extra tails, T.

copeland 2015-02-04 19:20:32
So you're tiling the circle with squares and dominoes.

copeland 2015-02-04 19:20:41
Something, something, Fibonacci, and then you're done.

liopoil 2015-02-04 19:21:00
that sounds more elegant

liopoil 2015-02-04 19:21:00
why didn't we do that?

copeland 2015-02-04 19:21:02
Meh.

copeland 2015-02-04 19:21:22
I thought this approach was a better illustration of the kinds of techniques you'd want at 10-22.

Seasend 2015-02-04 19:21:38
im sure the "squares and dominoes" would be faster and more efficient

copeland 2015-02-04 19:21:44
If you remember your Fibonacci numbers.

mayaabiram 2015-02-04 19:22:08
you mean 10-12

b4200010 2015-02-04 19:22:08
10-22?

Jwilson1990J 2015-02-04 19:22:08
whats 10-22

copeland 2015-02-04 19:22:10
AMC 10, Problem 22. Sorry.

copeland 2015-02-04 19:22:13
23. The zeros of the function $f(x) = x^2 - ax +2a$ are integers. What is the sum of the possible values of $a$?
$\phantom{peekaboo!}$
$\text{(A) } {7} \quad \text{(B) } {8} \quad \text{(C) } {16} \quad \text{(D) } {17} \quad \text{(E) } {18}$

copeland 2015-02-04 19:22:19
I've seen a lot of different solutions for this problem, so there are a lot of things we could start with.

copeland 2015-02-04 19:22:22
As good contest-taking students, what tool should we grab first?

DeathLlama9 2015-02-04 19:23:10
Vieta!

amburger66 2015-02-04 19:23:10
vieta's!

Gwena 2015-02-04 19:23:10
Vieta's formulas?

Ryukuxu 2015-02-04 19:23:10
vietas

bengals 2015-02-04 19:23:10
Vieta

prpaxson 2015-02-04 19:23:10
viete's formula for x+y and xy

aoommen1 2015-02-04 19:23:10
I wanted to use vietas formulas...not sure if thats right

johnguolex 2015-02-04 19:23:10
vieta's formulas?

copeland 2015-02-04 19:23:20
Vieta! If the roots are $u$ and $v$ then the linear term gives $u+v=a$ and $uv=2a.$ Let's hang on to that.

copeland 2015-02-04 19:23:20
\begin{align*}u+v&=a\\uv&=2a\end{align*}

copeland 2015-02-04 19:23:23
What do you want to do with that now?

ompatel99 2015-02-04 19:24:01
SFFT

Teddys123 2015-02-04 19:24:01
sfft

warrenwangtennis 2015-02-04 19:24:01
SFFT

6stars 2015-02-04 19:24:01
subtract the second from the first

Smiley-Faces-88 2015-02-04 19:24:01
substiturte

az_phx_brandon_jiang 2015-02-04 19:24:01
divide them

ExuberantGPACN 2015-02-04 19:24:01
Simon's Favorite Factoring Trick!

shakeNbake 2015-02-04 19:24:01
multiply first equation by 2 and set equal

Special_K 2015-02-04 19:24:01
divide

copeland 2015-02-04 19:24:11
Two approaches. Both are eliminating $a.$

copeland 2015-02-04 19:24:15
Some people may choose to divide and some may choose to subtract. Let's go through both methods really quickly.

copeland 2015-02-04 19:24:20
What do we worry about first when we divide?

az_phx_brandon_jiang 2015-02-04 19:24:43
divide by 0

fz0718 2015-02-04 19:24:43
0

Psionic 2015-02-04 19:24:43
u + v = 0

awesomethree 2015-02-04 19:24:43
0

bli1999 2015-02-04 19:24:43
0

jigglypuff 2015-02-04 19:24:43
divide by 0

johnguolex 2015-02-04 19:24:43
if something is 0

fluffyanimal 2015-02-04 19:24:43
a=0

MathStudent2002 2015-02-04 19:24:43
$a=0$

luillo1 2015-02-04 19:24:43
0

copeland 2015-02-04 19:24:45
We need to make sure not to miss any $a=0$ solutions. Is there a solution with $a=0$?

hibiscus 2015-02-04 19:25:24
Yesp.

swirlykick 2015-02-04 19:25:24
yes

alex31415 2015-02-04 19:25:24
Yes, u=v=0

blueduck1 2015-02-04 19:25:24
Yes

p2pcmlp 2015-02-04 19:25:24
yes

aswu 2015-02-04 19:25:24
yes

RocketSingh 2015-02-04 19:25:24
yes

flyrain 2015-02-04 19:25:24
u=0 and v=0 if you want that

NeilOnnsu 2015-02-04 19:25:24
Even if there were it wouldn't affect the sum

zmyshatlp 2015-02-04 19:25:24
yeah

jameswangisb 2015-02-04 19:25:24
Yes

b4200010 2015-02-04 19:25:24
but it won't matter anyways because 0 contributes nothing to the sum

jeremylu 2015-02-04 19:25:24
yea

Dukejukem 2015-02-04 19:25:24
Maybe, but it doesn't affect the sum of possible values

copeland 2015-02-04 19:25:27
Honestly, I don't care. We want the sum of all possible $a$ values so whether or not $a=0$ gets added to that sum is irrelevant. For funsies, $u=v=0$ does give $a=0$ as a solution.

copeland 2015-02-04 19:25:33
Now we assume $a\neq0$ and we divide. That gives\[\frac{u+v}{uv}=\frac{a}{2a}\] or

copeland 2015-02-04 19:25:34
\[\frac1u+\frac1v=\frac12.\]

copeland 2015-02-04 19:25:39
Alright, one of them has to be positive. Let's let $u$ be positive and explore.

copeland 2015-02-04 19:25:42
Can you solve\[\frac11+\frac1v=\frac12?\]

Tuxianeer 2015-02-04 19:25:55
v = -2

CornSaltButter 2015-02-04 19:25:55
v=-2

legolego 2015-02-04 19:25:55
-2

stan23456 2015-02-04 19:25:55
v=-2

mathtastic 2015-02-04 19:25:55
obvious v=-2

warrenwangtennis 2015-02-04 19:25:55
-2

hjl00 2015-02-04 19:25:55
-1/2

copeland 2015-02-04 19:25:59
$v=-2$ solves this. What is $a?$

wcao9311 2015-02-04 19:26:19
-1

elpers21 2015-02-04 19:26:19
-1

lucylai 2015-02-04 19:26:19
-1

Kevin100 2015-02-04 19:26:19
-1

flyrain 2015-02-04 19:26:19
-1

Ultimate_draco 2015-02-04 19:26:19
-1

copeland 2015-02-04 19:26:20
$a=u+v=-1.$

copeland 2015-02-04 19:26:23
Can you solve\[\frac12+\frac1v=\frac12?\]

cmw1234 2015-02-04 19:26:45
no

atd09 2015-02-04 19:26:45
no

SimonSun 2015-02-04 19:26:45
NOOOOO

brian22 2015-02-04 19:26:45
v=INFINITY

bomb427006 2015-02-04 19:26:45
no

ask2001 2015-02-04 19:26:45
no

viv7000 2015-02-04 19:26:45
no solution

MathCompetitor0606 2015-02-04 19:26:45
no

skimisgod 2015-02-04 19:26:45
no

copeland 2015-02-04 19:26:46
NO!

copeland 2015-02-04 19:26:47
Can you solve\[\frac13+\frac1v=\frac12?\]

bharatputra 2015-02-04 19:27:10
yes v=6

jfsn7 2015-02-04 19:27:10
v=6

MathematicsOfPi 2015-02-04 19:27:10
v = 6

danusv 2015-02-04 19:27:10
yes v=6

Blazefang 2015-02-04 19:27:10
6

GeorgCantor 2015-02-04 19:27:10
v=6

legozelda 2015-02-04 19:27:10
6

kapilak 2015-02-04 19:27:10
6

TheStrangeCharm 2015-02-04 19:27:10
yeah, classic, v - 6

bomb427006 2015-02-04 19:27:10
6, a=9

BFYSharks 2015-02-04 19:27:10
6

copeland 2015-02-04 19:27:14
$v=6$ solves this.

copeland 2015-02-04 19:27:16
$a=3+6=9.$

copeland 2015-02-04 19:27:18
Can you solve\[\frac14+\frac1v=\frac12?\]

tdeng 2015-02-04 19:27:40
4

thatmathgeek 2015-02-04 19:27:40
v = 4

briyellowduck 2015-02-04 19:27:40
4

Psionic 2015-02-04 19:27:40
v = 4

hibiscus 2015-02-04 19:27:40
4

leagueoflanguin 2015-02-04 19:27:40
4 !!!

owm 2015-02-04 19:27:40
v=4

blueflute19 2015-02-04 19:27:40
4

Deathranger999 2015-02-04 19:27:40
Yes, v = 4, a = 8.

Picroft 2015-02-04 19:27:40
v=4

mathymath 2015-02-04 19:27:40
Yes v=4

copeland 2015-02-04 19:27:54
$v=4$ solves this. In this case $a=u+v=4+4=8.$

copeland 2015-02-04 19:27:56
Gosh, this is going to take a while, right?

Tuxianeer 2015-02-04 19:28:20
nope we're done

elpers21 2015-02-04 19:28:20
that's all the solutions

bobispro5 2015-02-04 19:28:20
no youre done

Yumantimatter 2015-02-04 19:28:20
no, thats it

copeland 2015-02-04 19:28:22
Nope, we're actually done. As $u$ increases, $v$ decreases. Since we just hit the point where $u=v$ we are guaranteed not to find any new values of $a.$

copeland 2015-02-04 19:28:30
So what's the answer?

MathMaestro9 2015-02-04 19:28:57
8+9-1=16

imath2013 2015-02-04 19:28:57
16

IequalSmart 2015-02-04 19:28:57
16!

Deathranger999 2015-02-04 19:28:57
16

jkyman 2015-02-04 19:28:57
C 16

hwl0304 2015-02-04 19:28:57
C

yang2000 2015-02-04 19:28:57
C-16

copeland 2015-02-04 19:29:01
We want \[-1+9+8=\boxed{16}.\] The answer is C.

copeland 2015-02-04 19:29:07
Now for subtraction.

copeland 2015-02-04 19:29:08
\[uv-2(u+v)=2a-2\cdot a=0.\]

copeland 2015-02-04 19:29:18
What do we do with that?

mathway 2015-02-04 19:29:49
SFFT

geogirl08 2015-02-04 19:29:49
SFFT

math_cool 2015-02-04 19:29:49
SFFT

ompatel99 2015-02-04 19:29:49
SFFT

mjlove 2015-02-04 19:29:49
SFFT

shakeNbake 2015-02-04 19:29:49
simons fav factoring trick

NumberNinja 2015-02-04 19:29:49
SFFT

hnkevin42 2015-02-04 19:29:49
Simon's Favorite Factoring Trick

TheMaskedMagician 2015-02-04 19:29:49
Factor via SFFT

ninjataco 2015-02-04 19:29:49
use SFFT!

champion999 2015-02-04 19:29:49
SFFT it

copeland 2015-02-04 19:29:55
Simon's Favorite Factoring Trick! If we add 4 to both sides we get

copeland 2015-02-04 19:29:57
\[uv-2u-2v+4=4\] which now factors as \[(u-2)(v-2)=4.\]

copeland 2015-02-04 19:30:04
To clean things up, we could substitute $x=u-2$ and $y=v-2$ and now we want to find distinct $a=u+v=x+y+4$ given $xy=4.$

copeland 2015-02-04 19:30:08
Again we get

copeland 2015-02-04 19:30:10
\[\begin{array}{c|c|c}
x&y&x+y+4\\
\hline
4&1&9\\
2&2&8\\
1&4&9\\
-1&-4&-1\\
-2&-2&0\\
-4&-1&-1\\
\end{array}\]

copeland 2015-02-04 19:30:19
(Obviously some of those are redundant by symmetry.)

copeland 2015-02-04 19:30:21
We get the same possible values for $a$ so the answer is $-1+0+8+9=\boxed{16}.$ (C).

jkyman 2015-02-04 19:30:53
this way is easier

copeland 2015-02-04 19:30:54
Well, it was faster because I did it more quickly. I liked the fractions way because that's what I did.

copeland 2015-02-04 19:31:05
24. For some positive integers $p$, quadrilateral $ABCD$ with positive integer side lengths has perimeter $p$, right angles at $B$ and $C$, $AB = 2$, and $CD=AD$. How many different values of $p<2015$ are possible?
$\phantom{peekaboo!}$
$\text{(A) } {30} \quad \text{(B) } {31} \quad \text{(C) } {61} \quad \text{(D) } {62} \quad \text{(E) } {63}$

copeland 2015-02-04 19:31:22
Let's start by drawing a picture to get ourselves more comfortable with the problem.

danusv 2015-02-04 19:31:37
Draw a diagram!

ompatel99 2015-02-04 19:31:37
picture!

cellobix 2015-02-04 19:31:37
Draw a picture.

copeland 2015-02-04 19:31:40

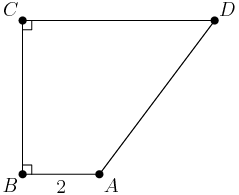
copeland 2015-02-04 19:31:44
Now we have a basic picture, but it isn't particularly enlightening.

copeland 2015-02-04 19:31:45
How could we improve this diagram?

retrovirus721 2015-02-04 19:32:24
label congruent sides

droid347 2015-02-04 19:32:24
label isoceles.

wlpj11 2015-02-04 19:32:24
you can label things

CornSaltButter 2015-02-04 19:32:24
label with, say x and y for the sides

RoboMan 2015-02-04 19:32:24
put values in for the reaining sides

copeland 2015-02-04 19:32:27
Since we're concerned with the perimeter, it makes sense to assign variables to the side lengths.

copeland 2015-02-04 19:32:27
The problem tells us that $CD=AD$, so we only need two variables for our three sides. We'll call $BC = x$ and $CD=AD=y$.

copeland 2015-02-04 19:32:30
So the perimeter is $p=2y + x + 2$.

copeland 2015-02-04 19:32:31

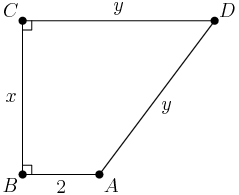
copeland 2015-02-04 19:32:33
At first, it may look like we can choose $x,y$ to be any positive integers such that $2y + x + 2 < 2015$. Why is that not actually the case?

jameswangisb 2015-02-04 19:33:17
line perpendicular to AB from A

SimonSun 2015-02-04 19:33:17
draw altudes!

AlcumusGuy 2015-02-04 19:33:17
draw altitude from A to CD

bobacadodl 2015-02-04 19:33:17
perpendicular from A to CD

Naysh 2015-02-04 19:33:17
Drop the altitude from $A$ to $CD$.

copeland 2015-02-04 19:33:22
$x$ and $y$ are related to each other. If we drop a perpendicular from $A$ to side $CD$, we see a right triangle that relates $x$ and $y$:

copeland 2015-02-04 19:33:24
What does the Pythagorean Theorem tell us?

copeland 2015-02-04 19:33:24

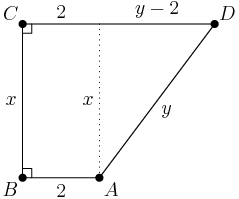
MathStudent2002 2015-02-04 19:33:52
x^2=y^2-(y-2)^2=4y+4

droid347 2015-02-04 19:33:52
$(y-2)^2+x^2=y^2$

brian22 2015-02-04 19:33:52

swirlykick 2015-02-04 19:33:52
must satisfy pyth. for x^2 + (y-2)^2 = y^2

Deathranger999 2015-02-04 19:33:52
Pythagorean theorem might be useful, (y-2)^2 + x^2 = y^2.

lucylai 2015-02-04 19:33:52
(y-2)^2+x^2=y^2

alex31415 2015-02-04 19:33:52
x^2+(y-2)^2=y^2

Duncanyang 2015-02-04 19:33:52
x^2+(y-2)^2=y^2

math0127 2015-02-04 19:33:52
y^2 = (y-2)^2 + x^2

Jayjayliu 2015-02-04 19:33:52
x^2+(y-2)^2=y^2

acsigaoyuan 2015-02-04 19:33:52
y^2=x^2+(y-2)^2

copeland 2015-02-04 19:33:55
By the Pythagorean Theorem, we have $(y-2)^2 + x^2 = y^2$. Or, after expanding both sides and rearranging, \[x^2 = 4y - 4 = 4(y-1)\]

copeland 2015-02-04 19:34:01
What does this tell us about $x$?

jigglypuff 2015-02-04 19:34:25
x is divisible by 2

warrenwangtennis 2015-02-04 19:34:25
it is even

kkpanu9 2015-02-04 19:34:25
it is even

jigglypuff 2015-02-04 19:34:25
x is even

az_phx_brandon_jiang 2015-02-04 19:34:25
must be even

Ramanan369 2015-02-04 19:34:25
x is even

Annabeth 2015-02-04 19:34:25
x is even

ExuberantGPACN 2015-02-04 19:34:25
x is even

jhshi07 2015-02-04 19:34:25
x must be even

aersoz 2015-02-04 19:34:25
x is even?

copeland 2015-02-04 19:34:27
The integer restriction tells us that $x$ is even, so we can write $x = 2z$.

copeland 2015-02-04 19:34:32
Plugging $x=2z$ into our equation, we see that $4z^2 = 4(y-1)$, or $y = z^2 + 1$.

copeland 2015-02-04 19:34:35
Now everything depends on our integer $z.$ What is the perimeter in terms of $z$?

ninjataco 2015-02-04 19:35:24
2z^2 + 2z + 4

acsigaoyuan 2015-02-04 19:35:24
2z^2+2z+4

flyrain 2015-02-04 19:35:24
2z^2+2z+4

ExuberantGPACN 2015-02-04 19:35:24
2z^2+2z+4

droid347 2015-02-04 19:35:24
2z^2+2z+4

CombatOmega 2015-02-04 19:35:24
2z^2 + 2z + 4

ChrisY 2015-02-04 19:35:24
2z+2z^2+4

Yumantimatter 2015-02-04 19:35:24
2z+2z^2+4

copeland 2015-02-04 19:35:26
The perimeter is
\begin{align*}
p &= 2y + x + 2 \\
&= 2(z^2 + 1) + 2z + 2 \\
&= 2z^2 + 2z + 4
\end{align*}

copeland 2015-02-04 19:35:28
Therefore, we simply need to count the positive integer $z$'s such that $2z^2 + 2z + 4 < 2015$.

copeland 2015-02-04 19:35:31
What is the largest possible $z$?

mathway 2015-02-04 19:35:56
31

trumpeter 2015-02-04 19:35:56
31

FractalMathHistory 2015-02-04 19:35:56
31

GU35T-31415 2015-02-04 19:35:56
31

p2pcmlp 2015-02-04 19:35:56
31

Abecissa 2015-02-04 19:35:56
31

QuadraticFanatic2416 2015-02-04 19:35:56
31

Tuxianeer 2015-02-04 19:35:56
31

atmath2011 2015-02-04 19:35:56
31

jslam 2015-02-04 19:35:56
31

MathematicsOfPi 2015-02-04 19:35:56
31

raidermath6 2015-02-04 19:35:56
31

copeland 2015-02-04 19:35:59
We're looking near $z^2\approx 1000.$ The square of 32 is $2^{10}=1024$ (powers of 2 anybody?), so when $z=32$, \[2z^2+2z+4 > 2\cdot1024=2048,\] so that's too big but just barely. The biggest value is probably 31.

copeland 2015-02-04 19:36:08
$31^2 = 961$, so plugging in $z = 31$ yields $2(961) + 2(31) + 4 = 1988 < 2015$.

copeland 2015-02-04 19:36:09
So the largest value of $z$ is 31.

copeland 2015-02-04 19:36:23
Since $x$ and $y$ are both positive integers, the smallest $z$ is 1.

copeland 2015-02-04 19:36:24
So what is our answer?

Studiosa 2015-02-04 19:36:43
B

CaptainFlint 2015-02-04 19:36:43
$\textbf{B}$

Duncanyang 2015-02-04 19:36:43
B

poweroftwo 2015-02-04 19:36:43
B

jigglypuff 2015-02-04 19:36:43
B) 31

briyellowduck 2015-02-04 19:36:43
B) 31

Psionic 2015-02-04 19:36:43
31

skimisgod 2015-02-04 19:36:43
B

yayups 2015-02-04 19:36:43
B

LMLM 2015-02-04 19:36:43
so the answer is B

WhaleVomit 2015-02-04 19:36:43
31

blueflute19 2015-02-04 19:36:43
31

copeland 2015-02-04 19:36:45
Our answer is (B) 31.

copeland 2015-02-04 19:37:22
Alright, one more problem from the 10.

copeland 2015-02-04 19:37:32
25. Let $S$ be a square of side length 1. Two points are chosen independently at random on the sides of $S$. The probability that the straight-line distance between the points
is at least $\frac{1}{2}$ is $\frac{a-b\pi}{c}$, where $a$, $b$, and $c$ are positive integers and $\gcd(a,b,c) = 1$. What is $a+b+c$?
$\phantom{peekaboo!}$
$\text{(A) } {59} \quad \text{(B) } {60} \quad \text{(C) } {61} \quad \text{(D) } {62} \quad \text{(E) } {63}$

copeland 2015-02-04 19:37:40
The way this problem is written, it kind of looks like it should be on the AIME. But don't let that scare you.

copeland 2015-02-04 19:37:43
We'll call the two points $A$ and $B$. (That way we have don't have to say the first and second point over and over again.)

copeland 2015-02-04 19:37:53
Let's start by looking at an example. Without loss of generality we can assume that our square has vertices $(0,0), (0,1), (1,0)$, and $(1,1)$.

copeland 2015-02-04 19:37:55
For our example, suppose $A$ is at $(0,3/4)$.

copeland 2015-02-04 19:37:58

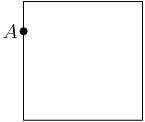
copeland 2015-02-04 19:38:14
Where can we place $B$ such that the straight-line distance between $A$ and $B$ is at least $1/2$?

zsp 2015-02-04 19:38:47
draw a circle

ninjataco 2015-02-04 19:38:47
outside the circle of radius 1/2 centered at A

Picroft 2015-02-04 19:38:47
Outside a circle of radius 1/2

LMLM 2015-02-04 19:38:47
We can draw a circle with radius of 1/2, and figure out where be can go

cellobix 2015-02-04 19:38:47
Outside of the circle of radius 1/2 centered around A.

bookworm2003 2015-02-04 19:38:47
anywhere inside the square and outside the circle with center A and radius 1/2

copeland 2015-02-04 19:38:52
If we draw a circle of radius $1/2$ centered at $A$, we want $B$ outside of this circle.

copeland 2015-02-04 19:38:55
We'll color these points in blue.

copeland 2015-02-04 19:38:56

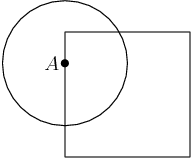
copeland 2015-02-04 19:38:57

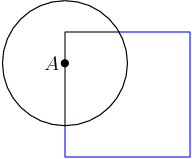
copeland 2015-02-04 19:39:08
Let's find the boundary points for the blue region.

copeland 2015-02-04 19:39:09
What is the boundary point on the left side of the square?

BFYSharks 2015-02-04 19:39:29
(0,1/4)

ompatel99 2015-02-04 19:39:29
(0,1/4)

swirlykick 2015-02-04 19:39:29
(0,1/4)

mjoshi 2015-02-04 19:39:29
(0, 1/4)

Destructio 2015-02-04 19:39:29
0, 1/4

amburger66 2015-02-04 19:39:29
(0,1/4)

atmchallenge 2015-02-04 19:39:29
(0,1/4)

hnkevin42 2015-02-04 19:39:29
(0, 1/4)

MathMaestro9 2015-02-04 19:39:29
0, 1/4

anandiyer12 2015-02-04 19:39:29
(0,1/4)

copeland 2015-02-04 19:39:31
The point is a distance of $1/2$ below $A$, so it is at $(0,1/4)$.

copeland 2015-02-04 19:39:37
By the Pythagorean Theorem, the second boundary point is at $(\sqrt{3}/4,1)$

copeland 2015-02-04 19:39:40
Let's calculate the probability that $B$ is in the successful region, given our assumption that $A$ is at $(0,3/4)$.

copeland 2015-02-04 19:39:43
Each side of the square looks a bit different, so we'll look at what happens on each side separately.

copeland 2015-02-04 19:39:52
What is the probability that $B$ is in the successful region if it is on the left side?

liopoil 2015-02-04 19:40:18
1/4

richy 2015-02-04 19:40:18
1/4

alex31415 2015-02-04 19:40:18
1/4

viv7000 2015-02-04 19:40:18
1/4

Empoleon2000 2015-02-04 19:40:18
1/4

Kevin100 2015-02-04 19:40:18
1/4

TigerLily14 2015-02-04 19:40:18
1/4

blueberry7 2015-02-04 19:40:18
1/4

CJaws 2015-02-04 19:40:18
1/4

bli1999 2015-02-04 19:40:18
1/4

copeland 2015-02-04 19:40:24
Since the boundary point on this side of the square is at $(0,1/4)$, the probability is $1/4$.

copeland 2015-02-04 19:40:26
The boundary point on the top of the square is at $(\sqrt{3}/4, 1)$, so the probability is $1 - \sqrt{3}/4$.

copeland 2015-02-04 19:40:36
And on the other two sides?

bomb427006 2015-02-04 19:40:54
1

jprogrammer 2015-02-04 19:40:54
1

amburger66 2015-02-04 19:40:54
1

mathmass 2015-02-04 19:40:54
1

acsigaoyuan 2015-02-04 19:40:54
1

hnkevin42 2015-02-04 19:40:54
1!

pearlm 2015-02-04 19:40:54
1 and 1

jkyman 2015-02-04 19:40:54
1

Empoleon2000 2015-02-04 19:40:54
1 and 1

Duncanyang 2015-02-04 19:40:54
1 on each

copeland 2015-02-04 19:40:59
Since the entire bottom and right sides are included in the successful region, the probability is 1 if $B$ is on one of those sides.

copeland 2015-02-04 19:41:02

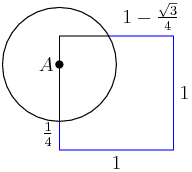
copeland 2015-02-04 19:41:04
The probability that $B$ is on any given side is $1/4$, so the probability that $B$ is chosen in the successful region in our example is \[\frac14\left[\frac{1}{4} + 1 + 1 + \left(1-\frac{\sqrt{3}}4\right)\right].\]

copeland 2015-02-04 19:41:13
All right, let's try to work in a little more generally. First of all, by symmetry, we can still assume that $A$ is on the left side of the square.

copeland 2015-02-04 19:41:20
Our example suggests that we might try examining what happens when $B$ is on each side of the square separately.

copeland 2015-02-04 19:41:23
What happens if $B$ is also chosen on the left side?

jigglypuff 2015-02-04 19:41:55
geometric probability

copeland 2015-02-04 19:41:59
OK, what do we draw?

az_phx_brandon_jiang 2015-02-04 19:43:03
We have -1/2<a-b<1/2

AlcumusGuy 2015-02-04 19:43:03

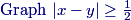
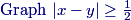
TigerLily14 2015-02-04 19:43:03
abs(a-b)>=1/2

cellobix 2015-02-04 19:43:03
A graph: position of A versus position of B. Draw the region where A and B are at least 1/2 apart.

liopoil 2015-02-04 19:43:03
it must have y-coordinate y_2 s.t. abs(y_1 - y_1) > 1/2

copeland 2015-02-04 19:43:12
In this case the problem becomes: If $a$ and $b$ are chosen uniformly at random in the interval $[0,1]$, what is the probability that $|a-b| \ge 1/2$?

copeland 2015-02-04 19:43:25
Let's see how that works out. The region we're working with is $0\le a\le1$ and $0\le b \le1$.

copeland 2015-02-04 19:43:27
What is the successful region for a pair $(a,b)$?

copeland 2015-02-04 19:43:28

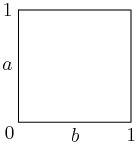
copeland 2015-02-04 19:43:50
As in, what does it look like?

ompatel99 2015-02-04 19:44:28
two triangles

MathStudent2002 2015-02-04 19:44:28
its the square except wth 2 1/2 x 1/2 right triangles removed at the top right and bottom left corners

mathymath 2015-02-04 19:44:28
Big long section that's diagonal in the middle

awe-sum 2015-02-04 19:44:28
two triangles

cellobix 2015-02-04 19:44:28
Mini triangles at the upper-left and lower-right corners.

GU35T-31415 2015-02-04 19:44:28
two triangles, one at the top left and one at the bottom right. They are 45-45-90, with legs of length 1/2

TigerLily14 2015-02-04 19:44:28
2 shaded triangles on top left and bottom right

AKAL3 2015-02-04 19:44:28
a square with triangular pieces chopped of at the upper left and lower right

copeland 2015-02-04 19:44:30
$(a,b)$ is successful if either $a \ge b + \frac{1}{2}$ or $a \le b - \frac{1}{2}$.

copeland 2015-02-04 19:44:33

copeland 2015-02-04 19:44:35
The area of this region is $\frac{1}{8} + \frac{1}{8} = \frac{1}{4}$.

copeland 2015-02-04 19:44:40
What happens if $B$ is chosen on the top side?

zsp 2015-02-04 19:45:06
This is harder

copeland 2015-02-04 19:45:10
It IS harder. . .

copeland 2015-02-04 19:45:27
So, assume $A=(0,a).$ What do we know about $B?$

liopoil 2015-02-04 19:46:05
$(1 - a)^2 + b^2 > 1/2

az_phx_brandon_jiang 2015-02-04 19:46:05
b is at (b,1)

fractal161 2015-02-04 19:46:05
point is (b, 1)

LMLM 2015-02-04 19:46:05
b,1

cellobix 2015-02-04 19:46:05
B = (b, 1) for 0<b<1

copeland 2015-02-04 19:46:12
And what do we do with those?

Studiosa 2015-02-04 19:46:36
distance formula

az_phx_brandon_jiang 2015-02-04 19:46:36
distance formula

LMLM 2015-02-04 19:46:36
$(1 - a)^2 + b^2 > 1/2$

ompatel99 2015-02-04 19:46:36
distance formula >=1/2

eswa2000 2015-02-04 19:46:36
do pythag

Eridan 2015-02-04 19:46:36
Pythagorean theorem

jslam 2015-02-04 19:46:36
distance formula

copeland 2015-02-04 19:46:39
Great.

copeland 2015-02-04 19:46:40
In this case, we can calculate the distance from $A$ to $B$. If we write $A = (0,a)$ and $B = (b,1)$, then the distance is $\sqrt{(1-a)^2 + b^2}$.

copeland 2015-02-04 19:46:45
$(a,b)$ is successful if $(1-a)^2 + b^2 \ge \frac 14$.

copeland 2015-02-04 19:46:45
What does that equation say geometrically?

aersoz 2015-02-04 19:47:20
outside of the circle

jigglypuff 2015-02-04 19:47:20
quarter circle

blueberry7 2015-02-04 19:47:20
circle!!

ACSIXueZiming 2015-02-04 19:47:20
the circle's radius?

LMLM 2015-02-04 19:47:20
equation of a circle like object?

viv7000 2015-02-04 19:47:20
its a circle?

Duncanyang 2015-02-04 19:47:20
that there is a circle

hnkevin42 2015-02-04 19:47:20
circle with radius 1/2

TigerLily14 2015-02-04 19:47:20
a circle with rad 1/2

trumpeter 2015-02-04 19:47:20
outside a circle

pedronr 2015-02-04 19:47:20
Outside the quarter circle in the top right

NeilOnnsu 2015-02-04 19:47:20
A quarter-circle with radius 1/2

copeland 2015-02-04 19:47:23
This says that we want $(a,b)$ to be outside the the region bounded by \[(1-a)^2+b^2=\left(\frac12\right)^2\] which is a circle of radius $\dfrac12$ centered at $(a,b)=(1,0).$

copeland 2015-02-04 19:47:26

copeland 2015-02-04 19:47:26
What is the area of the succesful region?

ompatel99 2015-02-04 19:48:04
1-pi/16

Duncanyang 2015-02-04 19:48:04
1-pi/16

mjoshi 2015-02-04 19:48:04
1-\pi/16

mathwrath 2015-02-04 19:48:04
1-pi/16

Anthrax 2015-02-04 19:48:04
1- 1/4(pi/4)

BFYSharks 2015-02-04 19:48:04
1-pi/16

flyrain 2015-02-04 19:48:04
1-pi/16

alex31415 2015-02-04 19:48:04
1-pi/16

bharatputra 2015-02-04 19:48:04
1-pi/16

copeland 2015-02-04 19:48:08
The bad region is a quarter circle with radius $\dfrac 12$, so the area of the successful region is $1 - \dfrac{\pi}{16}$.

copeland 2015-02-04 19:48:11
What happens if $B$ is chosen on the right side?

BFYSharks 2015-02-04 19:48:28
1

mathmass 2015-02-04 19:48:28
1

Eridan 2015-02-04 19:48:28
Probability of 1

poweroftwo 2015-02-04 19:48:28
prob. is 1

acsigaoyuan 2015-02-04 19:48:28
1

bli1999 2015-02-04 19:48:28
probability is 1

DeathLlama9 2015-02-04 19:48:28
1

pinkrock 2015-02-04 19:48:28
the probability is 1

Yumantimatter 2015-02-04 19:48:28
1, and on bottom too

jprogrammer 2015-02-04 19:48:28
1

AlcumusGuy 2015-02-04 19:48:28
probability is 1

hliu70 2015-02-04 19:48:28
all points work so 1

copeland 2015-02-04 19:48:30
This case is easy, $B$ can be anywhere on the right side, so the probability is 1!

copeland 2015-02-04 19:48:30
What happens if $B$ is chosen on the bottom side?

Psionic 2015-02-04 19:49:11
same

poweroftwo 2015-02-04 19:49:11
same as top

ACSIXueZiming 2015-02-04 19:49:11
same as the top side

az_phx_brandon_jiang 2015-02-04 19:49:11
same as top

DeathLlama9 2015-02-04 19:49:11
Same as top

jameswangisb 2015-02-04 19:49:11
same as top

amburger66 2015-02-04 19:49:11
same as if it's on the top side?

acsigaoyuan 2015-02-04 19:49:11
same as top side

viv7000 2015-02-04 19:49:11
1-pi/16

richy 2015-02-04 19:49:11
same as top

bomb427006 2015-02-04 19:49:11
same as top

yunyun333 2015-02-04 19:49:11
same as top m8

copeland 2015-02-04 19:49:13
This case is symmetric to the top side. The probability is again $1 - \dfrac{\pi}{16}$.

copeland 2015-02-04 19:49:17
All right. We've got every case individually, what is the probability?

jigglypuff 2015-02-04 19:50:18
26-pi/32

TheMaskedMagician 2015-02-04 19:50:18

TigerLily14 2015-02-04 19:50:18
(26-pi)/32

fclvbfm934 2015-02-04 19:50:18
$\frac{26 - \pi}{32}$

GU35T-31415 2015-02-04 19:50:18
It is 1/4 times the sum of the individual probabilities because each side is equally likely to be chosen. The probability is (26-pi)/32, so A

MathStudent2002 2015-02-04 19:50:18
1/2(1-pi/16)+1/4(1)+1/4(1/4)=(26-pi)/32

copeland 2015-02-04 19:50:21
Since each case occurs with probability $1/4$, the total probability is
\begin{align*}
\frac{1}{4}\left(\frac{1}{4} + 2 - \frac\pi8 + 1\right) &= \frac{2}{32} + \frac{16}{32} - \frac{\pi}{32} + \frac{8}{32} \\
&= \frac{26 - \pi}{32}
\end{align*}

copeland 2015-02-04 19:50:24
$a + b + c$ is $26 + 1 + 32 = 59$ and our answer is (A).

copeland 2015-02-04 19:50:31
Phew!

copeland 2015-02-04 19:50:36
All right, we're halfway done by some metric or other. Everyone stand up and spin in a circle really fast.

leagueoflanguin 2015-02-04 19:51:04
i will get too dizzy !!!

Psionic 2015-02-04 19:51:04
dizzy!

Destructio 2015-02-04 19:51:04
i is dizzy now

kmw2001 2015-02-04 19:51:04
now i am dizzy!

copeland 2015-02-04 19:51:06
Me too. SUCCESS!

copeland 2015-02-04 19:51:11
I'm feeling pretty good - let's keep going.

copeland 2015-02-04 19:51:14
I want to point out a couple of problems that people have mentioned before we move on to the AMC12.

copeland 2015-02-04 19:51:27
On the AMC10 we had this one:

copeland 2015-02-04 19:51:31
20. A rectangle has area $A \text{ cm}^2$ and perimeter $P \text{ cm}$, where $A$ and $P$ are positive integers. Which of the following numbers cannot equal $A+P?$
$\phantom{oops}$
(A) 100 (B) 102 (C) 104 (D) 106 (E) 108

copeland 2015-02-04 19:51:35
As you may know by now, this problem was unfortunately broken. It turns out that all the answer choices are possible values of $A+P$, because the problem statement forget the words in bold below:

copeland 2015-02-04 19:51:41
20. A rectangle with integer side lengths (in cm) has area $A \text{ cm}^2$ and perimeter $P \text{ cm}$, where $A$ and $P$ are positive integers. Which of the following numbers cannot equal $A+P?$
$\phantom{oops}$
(A) 100 (B) 102 (C) 104 (D) 106 (E) 108

copeland 2015-02-04 19:51:47
If we don't require that the sides have integer lengths, then we can make $A+P = n$ for any even $n > 4$ by letting the sides be 2 and $\frac{n}{4}-1$. Then the area is $A = \frac{n}{2}-2$, and the perimeter is $P = 2\left(2 + \frac{n}{4} - 1\right) = \frac{n}{2}+2$, so that $A+P = n.$

copeland 2015-02-04 19:52:01
To solve the intended version of the problem: let the sides be $r$ and $s$, which we assume are integers. Then $n = A+P = rs + 2(r+s).$

copeland 2015-02-04 19:52:09
Adding 4 to both sides invokes Simon's Favorite Factoring Trick:
\[
n+4 = rs + 2r + 2s + 4 = (r+2)(s+2).
\]

copeland 2015-02-04 19:52:15
So $n$ is possible using integer side lengths if and only if $n+4$ factors into two factors each larger than 2.

copeland 2015-02-04 19:52:20
All the choices other than (B) work: $104 = 4\cdot26,$ $108 = 4\cdot27,$ $110 = 10\cdot11,$ and $112 = 4\cdot28.$

copeland 2015-02-04 19:52:23
But (B) doesn't work, since $106 = 2\cdot53$ and 53 is prime.

copeland 2015-02-04 19:52:28
In the original (broken) version of the problem, a rectangle with sides 2 and 24.5 has area 49 and perimeter 53, which sum to 102. In fact, you can pick any reasonable value for $A$ and get whatever large-enough perimeter you want by varying the side lengths.

droid347 2015-02-04 19:53:18
What is the MAA going to do?

wangt 2015-02-04 19:53:18
so what happens to scores???

ompatel99 2015-02-04 19:53:18
What is MAA going to do about this?

mssmath 2015-02-04 19:53:18
What has the MAA decided regarding this problem?

AlcumusGuy 2015-02-04 19:53:18
What do you think will happen because of this typo/error?

copeland 2015-02-04 19:53:28
No idea, and I wouldn't want to speculate. I personally think that grading the problem still gives a good indicator of student ability so I would lean toward leaving it in.

copeland 2015-02-04 19:53:40
But my opinion isn't worth much. . .

copeland 2015-02-04 19:53:47
We also had 12A Problem 12:

copeland 2015-02-04 19:53:49
12. The parabolas $y=ax^2-2$ and $y=4-bx^2$ intersect the coordinate axes in exactly 4 points, and these four points are the vertices of a kite of area 12. What is $a+b?$
$\phantom{oops}$
(A) 1 (B) 1.5 (C) 2 (D) 2.5 (E) 3

copeland 2015-02-04 19:53:51
This problem is expecting you to draw this:

copeland 2015-02-04 19:53:57

copeland 2015-02-04 19:54:03
But. . .

2015WOOTer 2015-02-04 19:54:29
ohh, a, b>0, right?

ryanyoo 2015-02-04 19:54:29
a and b could be negatives

copeland 2015-02-04 19:54:31
However, there is an issue that you could have either $a$ or $b$ negative, like:

copeland 2015-02-04 19:54:34

copeland 2015-02-04 19:54:35
And still have 4 intersections.

copeland 2015-02-04 19:54:45
I found that if you notice the error here, you probably made the right course-correction pretty quickly. If either one is negative the largest value you can only get numbers less than 1 for $a+b$ so of the choices given, only 1.5 is even reasonable.

copeland 2015-02-04 19:54:58
The fix for this problem is probably to say that $a$ and $b$ are positive. I would bet that the real sentiment, though, was more like:

copeland 2015-02-04 19:55:02
12. The parabolas $y=ax^2-2$ and $y=4-bx^2$ intersect on the $x$-axis and intersect the coordinate axes in exactly 4 points. These four points are the vertices of a kite of area 12. What is $a+b?$
$\phantom{oops}$
(A) 1 (B) 1.5 (C) 2 (D) 2.5 (E) 3

hibiscus 2015-02-04 19:55:52
Does MAA usually make mistakes like this?

copeland 2015-02-04 19:55:55
Writing a test is REALLY HARD. I've written problems with errors before. You feel really bad about it. After all, you're trying to make something that is fun math for people.

copeland 2015-02-04 19:56:15
Let's move on. . .

copeland 2015-02-04 19:56:23
21. A circle of radius $r$ passes through both foci of, and exactly four points on, the ellipse with equation $x^2 + 16y^2 = 16.$ The set of all possible values of $r$ is an interval $[a,b).$ What is $a+b?$
$\phantom{Hi!}$
(A) $5\sqrt2 + 4$ (B) $\sqrt{17}+7$ (C) $6\sqrt2 + 3$ (D) $\sqrt{15}+8$ (E) 12

copeland 2015-02-04 19:56:26
First off, what does that notation $[a,b)$ mean?

2015WOOTer 2015-02-04 19:57:00
it means $a\le x<b$

FractalMathHistory 2015-02-04 19:57:00
a is inclusive, b is exclusive

acsigaoyuan 2015-02-04 19:57:00
a<=r<b

codyj 2015-02-04 19:57:00
$a\le r<b$

Duncanyang 2015-02-04 19:57:00
a <= x < b

thatmathgeek 2015-02-04 19:57:00
a <= ... < b

2015WOOTer 2015-02-04 19:57:00
it means $a\le r<b$

copeland 2015-02-04 19:57:03
It means that the possible values of $r$ satisfy $a \le r < b$. The bracket at the $a$ end means that we include $a$, but the parenthesis at the $b$ end means we don't include $b.$

copeland 2015-02-04 19:57:09
OH:

Anthrax 2015-02-04 19:57:11
Are we on 12A now?

Gwena 2015-02-04 19:57:11
Is this for the AMC 12?

copeland 2015-02-04 19:57:15
Yes. On to the AMC12.

copeland 2015-02-04 19:57:22
Let's start by sketching the ellipse. How?

zsp 2015-02-04 19:57:59
Draw x = 0 and y = 0

armalite46 2015-02-04 19:57:59
major axes 4 minor axes 1

hnkevin42 2015-02-04 19:57:59
Find the x and y-intercepts

alex31415 2015-02-04 19:57:59
The vertices are (0,1), (0,-1), (4,0), (-4,0)

lucylai 2015-02-04 19:57:59
it goes through (0,1),(0,-1),(4,0),(-4,0)

ninjataco 2015-02-04 19:57:59
centered at (0,0) horizontal axis length 8 and vertical axis length 2

copeland 2015-02-04 19:58:10
Let's look where it cross the axes.

copeland 2015-02-04 19:58:12
It passes through $(\pm4, 0)$ and $(0, \pm1).$ So it looks something like this:

copeland 2015-02-04 19:58:15

copeland 2015-02-04 19:58:15
Now what?

TheMaskedMagician 2015-02-04 19:58:29
Find the foci

mathymath 2015-02-04 19:58:29
Foci

skimisgod 2015-02-04 19:58:29
Find the foci

kcui 2015-02-04 19:58:29
the foci!

acsigaoyuan 2015-02-04 19:58:29
Find the foci

abvenkgoo 2015-02-04 19:58:29
fidn the foci

ACSIXueZiming 2015-02-04 19:58:29
find the foci

eswa2000 2015-02-04 19:58:29
find the foci

copeland 2015-02-04 19:58:31
We should probably find the foci, since all of our potential circles have to pass through the foci too.

copeland 2015-02-04 19:58:32
Wait, what are "foci"?

copeland 2015-02-04 19:58:39
Foci are focuses.

copeland 2015-02-04 19:58:47
Maybe "Foci is focuses." I don't know.

2015WOOTer 2015-02-04 19:59:19
we can find foci with the foci-distance equation

flyrain 2015-02-04 19:59:19
the points such that the sum of the distances to the foci is same for every point on the ellipse

Anthrax 2015-02-04 19:59:19
Points where the distance from one focus to the ellipse to the other focus is constant

MathStudent2002 2015-02-04 19:59:19
the sum of the distances to the foci is constant iirc

CreativeNinja 2015-02-04 19:59:21
focus on the foci

copeland 2015-02-04 19:59:24
One way to describe an ellipse is as all the points for which the sum of the distance to two foci is constant. (This is similar to a circle, in which the distance to a single point -- called the "center" -- is constant. A circle is also an ellipse where the foci are the same point.)

copeland 2015-02-04 19:59:26
The foci always lie at symmetric positions along the longer axis. So in our particular example, they lie at $(\pm f,0)$ for some $f$. And the total blue distance below is constant for any point on the ellipse:

copeland 2015-02-04 19:59:30

copeland 2015-02-04 19:59:30
But the point I chose as my example was a pretty dumb one. What's a smarter choice?

lucylai 2015-02-04 20:00:10
(4,0) and (0,1)

ninjataco 2015-02-04 20:00:10
(4,0)

Doink 2015-02-04 20:00:10
(4,0)

zsp 2015-02-04 20:00:10
4, 0

Picroft 2015-02-04 20:00:10
4,0

Studiosa 2015-02-04 20:00:10
(4,0)

BFYSharks 2015-02-04 20:00:10
(0,1) or (4,0)

acsigaoyuan 2015-02-04 20:00:11
(4,0)

copeland 2015-02-04 20:00:13
How about $(4,0)$?

copeland 2015-02-04 20:00:15
What is the total blue distance from $(4,0)$ to the two foci?

copeland 2015-02-04 20:00:15

sahilp 2015-02-04 20:00:38
8

jigglypuff 2015-02-04 20:00:38
8

GU35T-31415 2015-02-04 20:00:38
8

jkyman 2015-02-04 20:00:38
8

verum4one 2015-02-04 20:00:38
8

Psionic 2015-02-04 20:00:38
8

aopsish 2015-02-04 20:00:38
f+4 + (4-f) = 8

copeland 2015-02-04 20:00:40
The distance to the right focus is $4-f.$
The distance to the left focus is $4+f.$
So the total distance is 8.

copeland 2015-02-04 20:00:43
This means that for any point on the ellipse, the total blue distance is 8.

copeland 2015-02-04 20:00:44
So what?

copeland 2015-02-04 20:00:51
Oh, we wanted to do another one!

copeland 2015-02-04 20:00:57
Let's use the point $(0,1)$ as our example point:

copeland 2015-02-04 20:00:59
What's the total blue distance now?

copeland 2015-02-04 20:01:00

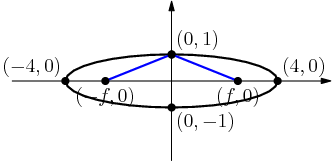
MathStudent2002 2015-02-04 20:01:38
The distance from (f,0) to (0,1) is 8/2=4, so our f is sqrt(15)

lucylai 2015-02-04 20:01:38
2sqrt(f^2+1)

acsigaoyuan 2015-02-04 20:01:38
2*sqrt(1+f^2)

ACSIXueZiming 2015-02-04 20:01:38
2 sqrt(f^2+1)

BFYSharks 2015-02-04 20:01:38
$2\sqrt{1+f^2}$

yimingz89 2015-02-04 20:01:38
2sqrt(f^2+1)=8

pedronr 2015-02-04 20:01:38
$2\sqrt{1+f^2}$

verum4one 2015-02-04 20:01:38
$2\sqrt{1+f^2}$

jameswangisb 2015-02-04 20:01:38
2(root(f^2+1))

copeland 2015-02-04 20:01:41
Each blue segment, by the Pythagorean Theorem, is $\sqrt{f^2 + 1}.$

copeland 2015-02-04 20:01:42
So the total blue distance is $2\sqrt{f^2+1},$ and this must equal 8.

copeland 2015-02-04 20:01:46
This means $\sqrt{f^2+1} = 4,$ so $f^2 + 1 = 16,$ and thus $f = \sqrt{15}.$

copeland 2015-02-04 20:01:53
So the foci are at $(\pm\sqrt{15},0).$

copeland 2015-02-04 20:01:55
My picture isn't very close to scale, so let's fix it up:

copeland 2015-02-04 20:01:57

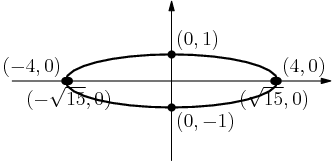
copeland 2015-02-04 20:02:01
Well...maybe that's too much to scale to be useful. So let's cheat a little and make it more readable:

hnkevin42 2015-02-04 20:02:10
whoa. they're close.

Duncanyang 2015-02-04 20:02:10
wow so close

copeland 2015-02-04 20:02:16

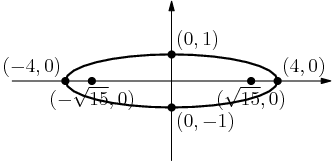
copeland 2015-02-04 20:02:28
OK, now what?

copeland 2015-02-04 20:02:28
What's the smallest circle that could possibly contain both foci and also 4 points on the ellipse?

blueberry7 2015-02-04 20:03:11
x^2+y^2=15

Jayjayliu 2015-02-04 20:03:11
One with radius sqrt(15)

zsp 2015-02-04 20:03:11
origin circle with radius sqrt15

acsigaoyuan 2015-02-04 20:03:11
diameter is between two foci

mathtastic 2015-02-04 20:03:11
one centered at the origin

Yumantimatter 2015-02-04 20:03:11
r=sqrt(15)

happyhummingbird 2015-02-04 20:03:11
radius = sqrt(15)

zacchro 2015-02-04 20:03:11
the one with radius $\sqrt{15}$

tanuagg13 2015-02-04 20:03:11
circle with radius root15 centered at origin

yajaniaj 2015-02-04 20:03:11
diameter of 2sqrt(15)

fractal161 2015-02-04 20:03:11
Circle of radius sqrt(15)

bomb427006 2015-02-04 20:03:11
x^2+y^2=15

GU35T-31415 2015-02-04 20:03:11
The one with the foci as endpoints of a diameter

nebulagirl 2015-02-04 20:03:11
r = sqrt(15)

copeland 2015-02-04 20:03:28
Note that the segment connecting the foci has to be a chord of our circle. So we want the smallest circle that contains a chord of length $2\sqrt{15}.$

copeland 2015-02-04 20:03:32
It's the circle with diameter $2\sqrt{15}$ --- any circle that's smaller won't have a big enough chord.

copeland 2015-02-04 20:03:33
So the smallest possible radius is $a = \sqrt{15}$:

copeland 2015-02-04 20:03:36

copeland 2015-02-04 20:03:38
(Note that the circle clearly intersects the ellipse at 4 points, so we're OK.)

copeland 2015-02-04 20:04:01
We notice 2 things:

Yumantimatter 2015-02-04 20:04:03
looks like Saturn!

hjl00 2015-02-04 20:04:03
that looks like saturn

flyrain 2015-02-04 20:04:03
looks like saturn

copeland 2015-02-04 20:04:07
and. . .

treemath 2015-02-04 20:04:12
already we see the answer is D

hnkevin42 2015-02-04 20:04:12
only one of our answer choices contains sqrt(15)...

copeland 2015-02-04 20:04:15
At this point, we know the answer is $\sqrt{15} + b$, where $b$ is the upper bound of the radius of the circle.

copeland 2015-02-04 20:04:26
Looking at the answer choices, I'd be very, very tempted to mark (D), since that's the only choice that has a $\sqrt{15}$ term. Otherwise, you'd have to believe that there's going to be a $-\sqrt{15}$ in $b$ to cancel it out, which seems unlikely.

copeland 2015-02-04 20:04:27
In fact, (D) is the answer! But let's see how we get $b=8$ to be our upper bound.

copeland 2015-02-04 20:04:30
What do we know about a circle that passes through both of $(\pm\sqrt{15},0)$?

swirlykick 2015-02-04 20:05:07
Its center is on the y axis

tiger21 2015-02-04 20:05:07
its center is on the y axis

cellobix 2015-02-04 20:05:07
It is on the y-axis

fractal161 2015-02-04 20:05:07
It has center on the y-axis.

jigglypuff 2015-02-04 20:05:07
centered on y axis

Doink 2015-02-04 20:05:07
its center lies on the y-axis

kaz74 2015-02-04 20:05:07
Center is on the y axis

copeland 2015-02-04 20:05:09
Its center must be on the $y$-axis.

copeland 2015-02-04 20:05:10
Specifically, if such a circle is centered at $(0,y)$, then the radius is $\sqrt{y^2+15}.$

copeland 2015-02-04 20:05:38
How can such a circle fail to intersect the ellipse in 4 points?

Hyperspace01 2015-02-04 20:06:29
if it touches the bottom or top of the ellipse in one point

az_phx_brandon_jiang 2015-02-04 20:06:29
tangent at the point (0,+-1)

ninjataco 2015-02-04 20:06:29
if it is above/below the ellipse

Kevin100 2015-02-04 20:06:29
if it only touches 3 points, such as if it hits "the bottom" of the ellipse

kcui 2015-02-04 20:06:29
if it is tangent to the top or bottom of the ellipse

smith_ch 2015-02-04 20:06:29
radius is not long enough to reach the bottom part of the elipse, so it only intersects in 2 points.

wlpj11 2015-02-04 20:06:29
it is centered to high or to low

awesomemathlete 2015-02-04 20:06:29
tangent to ellipse

copeland 2015-02-04 20:06:31
If it doesn't get "low enough" to reach the bottom half of the ellipse, like so:

copeland 2015-02-04 20:06:33

copeland 2015-02-04 20:06:34
But what's the point at which the bottom of the circle crosses the $y$-axis?

cellobix 2015-02-04 20:07:38
y - sqrt(y^2 + 15)

eswa2000 2015-02-04 20:07:38
(0, y-r)

verum4one 2015-02-04 20:07:38
$(0,y-\sqrt{y^2+15})$

ACSIXueZiming 2015-02-04 20:07:38
0,y-r

acsigaoyuan 2015-02-04 20:07:38
y-sqrt(y^2+15)

Anthrax 2015-02-04 20:07:38
(0, y-r)

kameswari 2015-02-04 20:07:38
y minus the radius?

copeland 2015-02-04 20:07:40
It's the point $(0,y-\sqrt{y^2+15}).$

copeland 2015-02-04 20:07:42
So for the circle to be "low enough" to work, we must have $y - \sqrt{y^2+15} < -1.$

copeland 2015-02-04 20:07:48
This rearranges to give $y+1 < \sqrt{y^2+15}.$

copeland 2015-02-04 20:07:50
Since $y>0$, it's safe to square both sides to get $y^2 + 2y + 1 < y^2 + 15.$

copeland 2015-02-04 20:07:54
Hence $2y < 14,$ or $y<7.$

copeland 2015-02-04 20:08:07
And when $y<7$, the radius is $\sqrt{y^2 + 15} < \sqrt{49 + 15} = \sqrt{64} = 8.$

ACSIXueZiming 2015-02-04 20:08:35
sqrt 15 +8

pedronr 2015-02-04 20:08:35
or 7+1

Duncanyang 2015-02-04 20:08:35
"D" IS THE ANSWER

copeland 2015-02-04 20:08:38
So the radius must be in the interval $[\sqrt{15},8)$ for the circle to work, and hence the answer is (D).

copeland 2015-02-04 20:08:51
Cool.

mango99 2015-02-04 20:09:03
that was a really looong solution

copeland 2015-02-04 20:09:04
You ain't seen nothing yet.

copeland 2015-02-04 20:09:14
22. For each positive integer $n,$ let $S(n)$ be the number of sequences of length $n$ consisting solely of the letters $A$ and $B,$ with no more than three $A$s in a row and no more than three $B$s in a row. What is the remainder when $S(2015)$ is divided by 12?
$\phantom{peekaboo!}$
$\text{(A) } {0} \quad \text{(B) } {4} \quad \text{(C) } {6} \quad \text{(D) } {8} \quad \text{(E) } {10}$

copeland 2015-02-04 20:09:19
I had a lot of great false-starts on this problem. My trouble was that I forgot the most important technique for solving contest problems. . .

Psionic 2015-02-04 20:09:43
DO SOMETHING

2015WOOTer 2015-02-04 20:09:43
small values!!

jigglypuff 2015-02-04 20:09:43
small cases

az_phx_brandon_jiang 2015-02-04 20:09:43
list out small cases?

TheMaskedMagician 2015-02-04 20:09:43
do stupid things?

ninjataco 2015-02-04 20:09:43
try small cases?

Psionic 2015-02-04 20:09:43
look for a pattern

hnkevin42 2015-02-04 20:09:43
start small.

MathStudent2002 2015-02-04 20:09:43
Let's try some small values of $n$ to see if we can find something

copeland 2015-02-04 20:09:46
Thank you.

copeland 2015-02-04 20:09:48
Try small cases.

copeland 2015-02-04 20:09:49
What is $S(1)$?

BFYSharks 2015-02-04 20:10:01
2

bobispro5 2015-02-04 20:10:01
2

hnkevin42 2015-02-04 20:10:01
2.

mathwrath 2015-02-04 20:10:01
2

lucylai 2015-02-04 20:10:01
2

wangt 2015-02-04 20:10:01
2

abvenkgoo 2015-02-04 20:10:01
2

Jayjayliu 2015-02-04 20:10:01
2

Yumantimatter 2015-02-04 20:10:01
2

tanuagg13 2015-02-04 20:10:01
2

Jayjayliu 2015-02-04 20:10:01
$2$

copeland 2015-02-04 20:10:03
$S(1)=2.$ We can either write $A$ or $B.$

copeland 2015-02-04 20:10:04
What is $S(2)?$

ompatel99 2015-02-04 20:10:15
4

bli1999 2015-02-04 20:10:15
4

eddy55 2015-02-04 20:10:15
4

Superwiz 2015-02-04 20:10:15
4

Abecissa 2015-02-04 20:10:15
4

yunyun333 2015-02-04 20:10:15
4

bubblebee412 2015-02-04 20:10:15
4

legolego 2015-02-04 20:10:15
4

bomb427006 2015-02-04 20:10:15
4

copeland 2015-02-04 20:10:17
$S(2)=4.$ We can have $\{AA,AB,BA,BB\}.$

copeland 2015-02-04 20:10:18
What is $S(3)?$

zsp 2015-02-04 20:10:36
8

Yumantimatter 2015-02-04 20:10:36
8

happyhummingbird 2015-02-04 20:10:36
8

yunyun333 2015-02-04 20:10:36
8

Duncanyang 2015-02-04 20:10:36
8

kaz74 2015-02-04 20:10:36
8

Hyperspace01 2015-02-04 20:10:36
8

Psionic 2015-02-04 20:10:36
8

skimisgod 2015-02-04 20:10:36
8

yajaniaj 2015-02-04 20:10:36
8

copeland 2015-02-04 20:10:38
$S(3)=8.$ We can have $\{AAA,AAB,ABA,ABB,BAA,BAB,BBA,BBB\}.$

copeland 2015-02-04 20:10:39
OK, so $S(n)=2^n.$ Clearly.

copeland 2015-02-04 20:10:43
No. . . that's wrong. You can usually put $A$ at the end, unless you already have 3 $A$s to begin with.

copeland 2015-02-04 20:10:50
Wait, there's an even deeper problem. There's a problem with naive recursion in that we can't just chop off the last character and talk in terms of $S(n-1)$. Is there something we can do?

dsyff 2015-02-04 20:12:05
cases

AlcumusGuy 2015-02-04 20:12:05
include earlier terms in the recursion

copeland 2015-02-04 20:12:10
How?

copeland 2015-02-04 20:12:30
How many different flavors of sequences are there? What certain ways can they end?

retrovirus721 2015-02-04 20:13:14
number of A's multiply by 2 for B

Dukejukem 2015-02-04 20:13:14
Define $T(n)$ as the number of sequences with length $n$, such that no three $A$'s or $B$'s are in a row, and the sequence ends in either two $A$'s or two $B$'s. Then define $R(n)$ as the number of sequences of length $n$, such that no three $A$'s or $B$'s are in a row, and the sequence ends in a single $A$ or $B.$ Then $S(n) = $T(n - 1) + 2R(n - 1).$ We can also find recur

alex31415 2015-02-04 20:13:14
A, AA, AAA, similar for B

cellobix 2015-02-04 20:13:14
3 in a row, 2 in a row, 1 in a row

acsigaoyuan 2015-02-04 20:13:14
end in 1, 2 or 3 consecutive letters

Studiosa 2015-02-04 20:13:14
A, AA, AAA, B, BB, BBB -- 6 possible endings

mssmath 2015-02-04 20:13:14
A,AA,AAA,B,BB,BBB

az_phx_brandon_jiang 2015-02-04 20:13:14
end in 0,1, or 2A's or 0, 1, or 2 B's

copeland 2015-02-04 20:13:25
We could instead chop off the last block of equal characters!

copeland 2015-02-04 20:13:31
We can get a valid string by taking any string of length $n$ and deleting as many identical characters as possible from the end of the string (1, 2, or 3).

copeland 2015-02-04 20:13:38
Therefore the strings of length $n$ ends in one of three ways:
* [$\cdots BA$] A single character of some parity following a string of length $n-1$ that ends in the opposite parity
* [$\cdots BAA$] Two characters of some parity following a string of length $n-2$ that ends in the opposite parity
* [$\cdots BAAA$] Three characters of some parity following a string of length $n-3$ that ends in the opposite parity

copeland 2015-02-04 20:13:54
Deleting as many identical characters as possible from the end of each of our strings of length $n$ gives a bijection between the set of strings of length $n$ and the union of the sets of strings of length $n-1,$ $n-2,$ and $n-3.$

copeland 2015-02-04 20:14:24
What recursive formula does that give us?

flyrain 2015-02-04 20:15:07
Tribonnaci

Psionic 2015-02-04 20:15:07
so S(n) = S(n-1) + S(n-2) + S(n-3)

az_phx_brandon_jiang 2015-02-04 20:15:07
S(n)=S(n-1)+S(n-2)+S(n-3)

flyrain 2015-02-04 20:15:07
S(n)=S(n-1)+S(n-2)+S(n-3)

lucylai 2015-02-04 20:15:07
S(n)=S(n-1)+S(n-2)+S(n-3)

Dukejukem 2015-02-04 20:15:07
It ends up being Fibonacci-esque I'm pretty sure

danusv 2015-02-04 20:15:07
S(n)=S(n-1)+S(n-2)+S(n-3)

amor13 2015-02-04 20:15:07
s(n) = s(n-1) + s(n-2) + s(n-3)

bobispro5 2015-02-04 20:15:07
s=s_n-1+s_n-2+s_n-3

acsigaoyuan 2015-02-04 20:15:07
S(n)=2S(n-1)+2S(n-2)+S(n-3)

swirlykick 2015-02-04 20:15:07
S(n)=s(n-1)+s(n-2)+s(n-3)?

eswa2000 2015-02-04 20:15:07

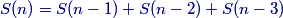
wehac 2015-02-04 20:15:07
s(n)=s(n-3)+s(n-2)+s(n-1)

copeland 2015-02-04 20:15:10
This tells us that

copeland 2015-02-04 20:15:11
\[S(n)=S(n-1)+S(n-2)+S(n-3).\]

copeland 2015-02-04 20:15:14
Now we just start listing. Fortunately we computed the first three already.

copeland 2015-02-04 20:15:17
\[\begin{array}{c|ccccc}
n &1&2&3& 4&5 \\
\hline
S(n)&2&4&8&14&26\\
\end{array}\]

copeland 2015-02-04 20:15:22
Oops. We only want that modulo 12. Let's try again:

copeland 2015-02-04 20:15:24
\[\begin{array}{c|cccccccccccccccccc}
n &1&2&3& 4&5 &6&7&8&9 &10&11&12&13&14&15&16&17&18\\
\hline
S(n)\pmod{12}&2&4&8&2 &2 &0&4&6&10&8 &0 &6 &2 & 8& 4& 2& 2&8\\
\end{array}\]

copeland 2015-02-04 20:15:31
And when I was working the test myself I got even further than this before saying to myself, "Jeremy, what you are doing is stupid."

copeland 2015-02-04 20:15:38
What is the right way to do this?

mssmath 2015-02-04 20:16:13
Take mod 3 and mod 4 is easier

lucylai 2015-02-04 20:16:13
mod 3 and mod 4

tanuagg13 2015-02-04 20:16:13
mod 3, mod 4

danusv 2015-02-04 20:16:13
mod 3 and mod 4 and then use CRT

hnkevin42 2015-02-04 20:16:13
split it up into mod 3 and mod 4

Special_K 2015-02-04 20:16:13
mod 3 and mod 4

Hydroxide 2015-02-04 20:16:13
Take mod 3 and mod 4

awesomemathlete 2015-02-04 20:16:13
remainders modulo 3 and 4

copeland 2015-02-04 20:16:16
Of course we want the Chinese Remainder Theorem. We should look at the sequence modulo 3 and 4 separately and see what happens. What is the period modulo 3?

awesomemathlete 2015-02-04 20:17:20
13

Hydroxide 2015-02-04 20:17:20
13

awesomemathlete 2015-02-04 20:17:20
the period is 13 modulo 3

lucylai 2015-02-04 20:17:20
1,2,1,1,1,0,2,0,2,1,0,0,1 => period is 13

acsigaoyuan 2015-02-04 20:17:20
13

ompatel99 2015-02-04 20:17:20
13

zacchro 2015-02-04 20:17:20
13

copeland 2015-02-04 20:17:23
\[\begin{array}{c|ccccccccccccc|cccc}
n &1&2&3& 4&5 &6&7&8&9 &10&11&12&13&14&15&16&17&18\\
\hline
S(n)\pmod{3}&2&1&2&2 &2 &0&1&0&1 &2 &0 &0 &2 & 2& 1& 2& 2&2\\
\end{array}\]

copeland 2015-02-04 20:17:26
We've hit a block of 3 that repeats (212). Since there are 3 terms to the recursion that tells us that we have to start repeating here.

copeland 2015-02-04 20:17:32
The period modulo 3 is 13. What is the period modulo 4?

acsigaoyuan 2015-02-04 20:18:09
4

zacchro 2015-02-04 20:18:09
4

lucylai 2015-02-04 20:18:09
4

apple.singer 2015-02-04 20:18:09
it's 4

ompatel99 2015-02-04 20:18:09
4

pedronr 2015-02-04 20:18:09
4

verum4one 2015-02-04 20:18:09
4

Psionic 2015-02-04 20:18:09
4

copeland 2015-02-04 20:18:11
\[\begin{array}{c|cccc|cccc|cccc|cccc|cc}
n &1&2&3& 4&5 &6&7&8&9 &10&11&12&13&14&15&16&17&18\\
\hline
S(n)\pmod{4}&2&0&0&2 &2 &0&0&2&2&0 &0 &2 &2 & 0& 0& 2& 2&0\\
\end{array}\]

copeland 2015-02-04 20:18:12
The period is 4.

niraekjs 2015-02-04 20:18:19
You can also do it mod 12, but that sequence would be about 50 long, eh? :p

copeland 2015-02-04 20:18:20
(The period mod 12 is 52. That would have taken a while.)

copeland 2015-02-04 20:18:23
And you all memorized the factorization of 2015, right?

az_phx_brandon_jiang 2015-02-04 20:18:40
5*31*13

lucylai 2015-02-04 20:18:40
5*13*31

BlankeSlayer 2015-02-04 20:18:40
5+31+13

Duncanyang 2015-02-04 20:18:40
yes 5 * 13 * 31

poweroftwo 2015-02-04 20:18:40
5x13x31

abvenkgoo 2015-02-04 20:18:40
5*13*31

kcui 2015-02-04 20:18:40
5*13*31

spin8 2015-02-04 20:18:40
5*31*15

BFYSharks 2015-02-04 20:18:40
3*5*31

AlcumusGuy 2015-02-04 20:18:40
5*13*31

yunyun333 2015-02-04 20:18:40
5*13*31

MathStudent2002 2015-02-04 20:18:40
5*13*31

copeland 2015-02-04 20:18:51
$2015=13\cdot31\cdot5.$

copeland 2015-02-04 20:18:53
So \[S(2015)\equiv S(13)\equiv 2\pmod{3}.\]
Also, \[S(2015)=S(2012+3)\equiv S(3)\equiv 0\pmod4.\]

copeland 2015-02-04 20:18:56
What does that make $S(2015)\pmod{12}?$

GU35T-31415 2015-02-04 20:19:22
8

DrMath 2015-02-04 20:19:22
8

Studiosa 2015-02-04 20:19:22
D -- 8

butter67 2015-02-04 20:19:22
8

vinayak-kumar 2015-02-04 20:19:22
8

Tuxianeer 2015-02-04 20:19:22
8

bharatputra 2015-02-04 20:19:22
8

happyhummingbird 2015-02-04 20:19:22
8?

bli1999 2015-02-04 20:19:22
8

copeland 2015-02-04 20:19:24
This makes $S(2015)\equiv\boxed8\pmod{12}.$ The answer is D.

masad24 2015-02-04 20:19:28
wait since when did we have to memorize that? >v<

copeland 2015-02-04 20:19:37
I think it's in the AMC rulebook.

copeland 2015-02-04 20:19:54
Just to mess with your mind, it should be the case that $S(0)=1$ since there is one empty word. However if we backsolve
\begin{align*}
S(3)&=S(2)+S(1)+S(0)\\
8&=4+2+S(0)\\
\end{align*}
we get $S(0)=2.$

copeland 2015-02-04 20:20:00
What happened?

BlankeSlayer 2015-02-04 20:20:48
you could have an empty a and empty B

lcalvert99 2015-02-04 20:20:48
a 0 times and b 0 times

jigglypuff 2015-02-04 20:20:48
you can pretend it ends in a or ends in b

fluffyanimal 2015-02-04 20:20:51
You can either have 0 as or 0 bs?

copeland 2015-02-04 20:20:52
For the sake of this problem there are TWO empty words, the one that ends with $A$ and the one that ends with $B$. Specifically, this two counts the words you get from deleting the ends of $AAA$ and $BBB$. We construct these from the empty word that ends with $B$ and the empty word that ends with $A,$ respectively.

copeland 2015-02-04 20:21:18
Hey, freebie time!

copeland 2015-02-04 20:21:19
Problem 23 on the AMC 12 is the same as Problem 25 on the AMC 10.

copeland 2015-02-04 20:21:24
Everybody do the freebie dance!

copeland 2015-02-04 20:21:34
and. . .

copeland 2015-02-04 20:21:37
stop.

copeland 2015-02-04 20:21:40
24. Rational numbers $a$ and $b$ are chosen at random among all rational numbers in the interval $[0,2)$ that can be written as fractions $\dfrac nd$ where $n$ and $d$ are integers with $1\leq d\leq 5.$ What is the probability that \[\left(\cos(a\pi)+i\sin(b\pi)\right)^4\] is a real number?
$\phantom{peekaboo!}$
$\text{(A) } {\dfrac3{50}} \quad \text{(B) } {\dfrac4{25}} \quad \text{(C) } {\dfrac{41}{200}} \quad \text{(D) } {\dfrac6{25}} \quad \text{(E) } {\dfrac{13}{50}}$

copeland 2015-02-04 20:22:09
So far we only have cosine of $a\pi$ and sine of $b\pi.$ Let's agree to define \[c=\cos( a\pi)\]and\[ s=\sin( b\pi)\]so that it is easier for you. I will continue to write the full expressions.

copeland 2015-02-04 20:22:21
How do I know when a number is real?

ninjataco 2015-02-04 20:22:45
imaginary part is equal to 0

junat3 2015-02-04 20:22:45
imaginary component is zero

az_phx_brandon_jiang 2015-02-04 20:22:45
imaginary part = 0

amor13 2015-02-04 20:22:45
if x + iy and y = 0

Dukejukem 2015-02-04 20:22:45
When it's imaginary part is equal to $0$

mssmath 2015-02-04 20:22:45
Imaginary part is zero

mathtastic 2015-02-04 20:22:45
imaginary part=0

SHARKYBOY 2015-02-04 20:22:45
if the coefficient of the i term is 0

copeland 2015-02-04 20:22:49
A number is real when its imaginary part is 0. What is the imaginary part of \[\left(\cos(a\pi)+i\sin(b\pi)\right)^4?\]

acsigaoyuan 2015-02-04 20:24:33
4ab^3+4ba^3

MathStudent2002 2015-02-04 20:24:33
sin(b*pi)*cos^3(a*pi)-sin^3(b*pi)*cos(a*pi)

ompatel99 2015-02-04 20:24:33
4c^3s-4cs^3

fluffyanimal 2015-02-04 20:24:33
4cs(c^2-s^2)

kingsave3166 2015-02-04 20:24:33
sin(bpi)*cos^3(api) - sin^3(bpi)*cos(api)?

wehac 2015-02-04 20:24:33
cos^3(api)sin(bpi)-cos(api)sin^3(bpi)

copeland 2015-02-04 20:24:36
The Binomial Theorem gives\[(c+is)^4=c^4+4ic^3s-6c^2s^2-4ics^3+s^4.\]

copeland 2015-02-04 20:24:38
The imaginary part (with an $i$ included) is \[4i\cos^3(a\pi)\sin(b\pi)-4i\cos(a\pi)\sin^3(b\pi).\]

copeland 2015-02-04 20:24:43
What do we do with that?

codyj 2015-02-04 20:25:04
=0

Psionic 2015-02-04 20:25:04
set = 0

Duncanyang 2015-02-04 20:25:04
set it equal to 0

mathtastic 2015-02-04 20:25:04
want that mess to be 0

az_phx_brandon_jiang 2015-02-04 20:25:04
c^3*s-c*s^3=0

GU35T-31415 2015-02-04 20:25:04
set it equal to 0

ACSIXueZiming 2015-02-04 20:25:04
make it be 0

copeland 2015-02-04 20:25:05
We want when this is zero.

chessderek 2015-02-04 20:25:12
factor

hwang2001 2015-02-04 20:25:12
factor out 4i

Studiosa 2015-02-04 20:25:12
factor

eddy55 2015-02-04 20:25:12
factor out 4i*cs

flyrain 2015-02-04 20:25:12
factor

Andre1228 2015-02-04 20:25:12
factor

pedronr 2015-02-04 20:25:12
factor

copeland 2015-02-04 20:25:16
And we can factor it. First, since we only want to know when this is zero we can drop the $4i.$ Then we want to solve \[\cos(a\pi)\sin(b\pi)\left[\cos(a\pi)-\sin(b\pi)\right]\left[\cos(a\pi)+\sin(b\pi)\right]=0.\]

copeland 2015-02-04 20:25:21
Therefore we want all solutions to any of the equations
\begin{align*}
(A)\qquad\cos(a\pi)&=0\\
(B)\qquad\sin(b\pi)&=0\\
(C')\qquad\cos(a\pi)&=\sin(b\pi)\\
(C'')\qquad\cos(a\pi)&=-\sin(b\pi)
\end{align*}

copeland 2015-02-04 20:25:26
Since the signs of trig functions are always a bit annoying, let's combine those last two, giving us cases (A), (B), and (C):

copeland 2015-02-04 20:25:27
We want all solutions to any of the equations
\begin{align*}
(A)\qquad\cos(a\pi)&=0\\
(B)\qquad\sin(b\pi)&=0\\
(C)\qquad\cos(a\pi)&=\pm\sin(b\pi)\\
\end{align*}

copeland 2015-02-04 20:25:37
That was algebra. There's a geometric interpretation to the 4th power of a number being real. What is that?

Superwiz 2015-02-04 20:26:03
Roots of unity!

EulerMacaroni 2015-02-04 20:26:03
dem roots of unity

copeland 2015-02-04 20:26:04
That's "4th power being 1."

Dukejukem 2015-02-04 20:26:39
The argument of the complex number must be a multiple of $\frac{\pi}{4}$

acsigaoyuan 2015-02-04 20:26:39
the angle is a multiple of pi/4

kingsave3166 2015-02-04 20:26:39
a cross?

mssmath 2015-02-04 20:26:39
it has arguement of 45,90,135,180,..

copeland 2015-02-04 20:26:41
If a number's fourth power is real, its argument is an integer multiple of $\dfrac\pi4.$ That means when we plot it in the complex plane it is on one of the four lines:

copeland 2015-02-04 20:26:45

copeland 2015-02-04 20:26:59
Not surprising. . . we have 4 lines algebraically as well.

copeland 2015-02-04 20:27:01
Now that we have that, let's switch gears. This is another probability problem. This looks like a $\dfrac{\text{success}}{\text{total}}$ type of computation. Let's nail down that 'total' part. How many values can $a\pi$ take?

az_phx_brandon_jiang 2015-02-04 20:28:50
20

acsigaoyuan 2015-02-04 20:28:50
20

jigglypuff 2015-02-04 20:28:50
20

Yumantimatter 2015-02-04 20:28:50
20

hnkevin42 2015-02-04 20:28:50
20?

copeland 2015-02-04 20:28:52
There are 20 possible values. I will arrange them by denominator.

copeland 2015-02-04 20:28:57

copeland 2015-02-04 20:29:00
Likewise, $b\pi$ can take these 20 values.

copeland 2015-02-04 20:29:03
The rest of the problem is clever checking and clever bookkeeping. Here at the office we found the bookkeeping on this problem to be really frustrating so I will do things a little more carefully than you might be expecting.

copeland 2015-02-04 20:29:13
First let's get the values of these trig functions into a table so we have something common that we can point at.

copeland 2015-02-04 20:29:20

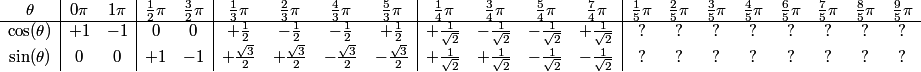
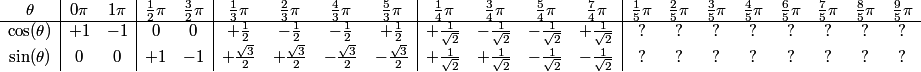
copeland 2015-02-04 20:29:32
You can double-click that to keep it around.

masad24 2015-02-04 20:29:34
why is it so tiny?

copeland 2015-02-04 20:29:38
Maybe this is better:

copeland 2015-02-04 20:29:55
\[\begin{array}{c|cc|cc|cccc|cccc|cccccccc}
\theta&
0\pi&1\pi&
\frac12\pi&\frac32\pi&
\frac13\pi&\frac23\pi&\frac43\pi&\frac53\pi&
\frac14\pi&\frac34\pi&\frac54\pi&\frac74\pi&\frac15\pi&\frac25\pi&\frac35\pi&\frac45\pi&\frac65\pi&\frac75\pi&\frac85\pi&\frac95\pi\\
\hline
\cos(\theta)&
+1&-1&
0&0&
+\frac12&-\frac12&-\frac12&+\frac12&
+\frac1{\sqrt2}&-\frac1{\sqrt2}&-\frac1{\sqrt2}&+\frac1{\sqrt2}&
?&?&?&?&?&?&?&?
\\
\sin(\theta)&
0&0&
+1&-1&
+\frac{\sqrt{3}}2&+\frac{\sqrt{3}}2&-\frac{\sqrt{3}}2&-\frac{\sqrt{3}}2&
+\frac1{\sqrt2}&+\frac1{\sqrt2}&-\frac1{\sqrt2}&-\frac1{\sqrt2}&
?&?&?&?&?&?&?&?
\\
\end{array}\]

copeland 2015-02-04 20:30:23
OK, I may post images two times a couple more times later in this problem, too.

copeland 2015-02-04 20:30:29
I don't know those fifths off-hand. I know that it's something-something-golden-ratio-something, but I really want to believe that we're not going to need to go that far.

copeland 2015-02-04 20:30:39
Now let's look at our conditions. For how many pairs $(a\pi,b\pi)$ is (A) $\cos(a\pi)=0$ satisfied?

trumpeter 2015-02-04 20:31:07
2

acsigaoyuan 2015-02-04 20:31:07
2

kingsave3166 2015-02-04 20:31:07
2

bobispro5 2015-02-04 20:31:07
2

ompatel99 2015-02-04 20:31:07
2

Duncanyang 2015-02-04 20:31:07
2

copeland 2015-02-04 20:31:12
It's on the table twice.

copeland 2015-02-04 20:31:22
How many (a,b) pairs satisfy this equation, though?

swirlykick 2015-02-04 20:31:48
2*20

zacchro 2015-02-04 20:31:48
40

kingsave3166 2015-02-04 20:31:48
oh actuall 2 * 20 = 40 right?

hnkevin42 2015-02-04 20:31:48
40?

bobispro5 2015-02-04 20:31:48
40

trumpeter 2015-02-04 20:31:48
actually 2*20=40

Dukejukem 2015-02-04 20:31:48
$2 \times 20 = 40$

lucylai 2015-02-04 20:31:48
40

zacchro 2015-02-04 20:31:48
40

tanuagg13 2015-02-04 20:31:48
40

ninjataco 2015-02-04 20:31:48
40

copeland 2015-02-04 20:31:54
This happens 20 times for each of $a\pi=\dfrac\pi2$ and $a\pi=\dfrac{3\pi}2.$ That's 40 total.

copeland 2015-02-04 20:31:56
Here I'm going to make another table. I'm going to let the first column be the possible values of $a\pi$ and then I want to list all of the successful $b\pi$ that go with each $a\pi.$

copeland 2015-02-04 20:31:59
You should get used to organizing things in tables for the AMC and AIME.

copeland 2015-02-04 20:32:04

copeland 2015-02-04 20:32:11
Small again or alright?

copeland 2015-02-04 20:32:31
\[\begin{array}{c|c}
a\pi&\cos(a\pi)=0\\
\hline
0\pi&\\
1\pi&\\
\hline
\frac12\pi&\text{all 20}\\
\frac32\pi&\text{all 20}\\
\hline
\frac13\pi&\\
\frac23\pi&\\
\frac43\pi&\\
\frac53\pi&\\
\hline
\frac14\pi&\\
\frac34\pi&\\
\frac54\pi&\\
\frac74\pi&\\
\hline
\frac15\pi&\\
\frac25\pi&\\
\frac35\pi&\\
\frac45\pi&\\
\frac65\pi&\\
\frac75\pi&\\
\frac85\pi&\\
\frac95\pi&\\
\end{array}\]

copeland 2015-02-04 20:32:45
How many times is $\sin(b\pi)=0?$

lucylai 2015-02-04 20:33:27
40

cellobix 2015-02-04 20:33:27
40 times.

trumpeter 2015-02-04 20:33:27
same as before, 40

IceFireGold1 2015-02-04 20:33:27
40

copeland 2015-02-04 20:33:29
This happens when $b\pi=0$ and $b\pi=\pi.$ That's another $20+20.$ So we're at 80 now?

Dukejukem 2015-02-04 20:34:17
$2 \times 20 = 40$, but now we're overcounting some cases when $\sin(b\pi) = 0$ and $\cos (a\pi) = 0$

kingsave3166 2015-02-04 20:34:17
40 times, but intersected 4 times so add 36

acsigaoyuan 2015-02-04 20:34:17
76

zacchro 2015-02-04 20:34:17
76

treemath 2015-02-04 20:34:17
overcounted

acsigaoyuan 2015-02-04 20:34:17
4 cases are repeated, so 76

lucylai 2015-02-04 20:34:17
subtract 4 for overcounting

pedronr 2015-02-04 20:34:17
no, double counted api=bpi=0

bobispro5 2015-02-04 20:34:17
4 repeats to be exact

Dukejukem 2015-02-04 20:34:17
We've overcounted four cases when $\sin (b\pi) = \cos (a\pi) = 0.$

copeland 2015-02-04 20:34:20
No. 4 of those intersect. We are 76 now. (I'll put the 4 repeats in red.)

copeland 2015-02-04 20:34:23

copeland 2015-02-04 20:34:33
Now we need to consider when $\cos(a\pi)=\pm\sin(b\pi).$ Let's do this by denominator.

copeland 2015-02-04 20:34:35
Here is our table of values again:

copeland 2015-02-04 20:34:39
\[\begin{array}{c|cc|cc|cccc|cccc|cccccccc}
\theta&
0\pi&1\pi&
\frac12\pi&\frac32\pi&
\frac13\pi&\frac23\pi&\frac43\pi&\frac53\pi&
\frac14\pi&\frac34\pi&\frac54\pi&\frac74\pi&\frac15\pi&\frac25\pi&\frac35\pi&\frac45\pi&\frac65\pi&\frac75\pi&\frac85\pi&\frac95\pi\\
\hline
\cos(\theta)&
+1&-1&
0&0&
+\frac12&-\frac12&-\frac12&+\frac12&
+\frac1{\sqrt2}&-\frac1{\sqrt2}&-\frac1{\sqrt2}&+\frac1{\sqrt2}&
?&?&?&?&?&?&?&?
\\
\sin(\theta)&
0&0&
+1&-1&
+\frac{\sqrt{3}}2&+\frac{\sqrt{3}}2&-\frac{\sqrt{3}}2&-\frac{\sqrt{3}}2&
+\frac1{\sqrt2}&+\frac1{\sqrt2}&-\frac1{\sqrt2}&-\frac1{\sqrt2}&
?&?&?&?&?&?&?&?
\\
\end{array}\]

copeland 2015-02-04 20:34:48
When the denominator of $a$ is 1 when do we get $\cos(a\pi)=\sin(b\pi)?$

kingsave3166 2015-02-04 20:35:55
4

gxah 2015-02-04 20:35:55
pi/4, 5pi/4

acsigaoyuan 2015-02-04 20:35:55
a=0, b= 1/2 or a=1,b= 3/2

mihirb 2015-02-04 20:35:55
Twice?

bobispro5 2015-02-04 20:35:55
4 cases

copeland 2015-02-04 20:36:00
This is good, let's expand that.

copeland 2015-02-04 20:37:22
When the denominator of $a$ is 1 we have $\cos=\pm1.$

copeland 2015-02-04 20:37:26
When is $\sin=\pm1?$

gxah 2015-02-04 20:37:59
0 or pi

bobispro5 2015-02-04 20:37:59
it is multiple of pi

fredgauss 2015-02-04 20:37:59
at \pi or at 0.

happyhummingbird 2015-02-04 20:37:59
0pi pi

acsigaoyuan 2015-02-04 20:37:59
b=1/2, 3/2

bli1999 2015-02-04 20:37:59
b=1/2 or 3/2

EulerMacaroni 2015-02-04 20:37:59
pi/2, 3pi/2

copeland 2015-02-04 20:38:02
We get that exactly when the denominator of $b$ is 2.

copeland 2015-02-04 20:38:04
When the denominator of $a$ is 2 when do we get $\cos(a\pi)=\sin(b\pi)?$

EulerMacaroni 2015-02-04 20:38:59
when b is an integer

bobispro5 2015-02-04 20:38:59
denominator of b is 1

acsigaoyuan 2015-02-04 20:38:59
b=0 or 1

Happytycho 2015-02-04 20:38:59
b=1 or b=0

copeland 2015-02-04 20:39:01
. . .and. . .

lucylai 2015-02-04 20:39:04
we've already counted these cases

copeland 2015-02-04 20:39:07
We get that exactly when the denominator of $b$ is 1.

copeland 2015-02-04 20:39:09
OK, let's put those on our chart. I'm putting the 4 we already counted in red again.

copeland 2015-02-04 20:39:13

copeland 2015-02-04 20:39:45
What about when the denominator is 3?

copeland 2015-02-04 20:39:51
When the denominator is 3 we have $|\cos(a\pi)|=\frac12$ but we always have $|\sin(b\pi)|=\frac{\sqrt3}2.$ That's weird. What happened?

flyrain 2015-02-04 20:40:25
it's just the nature of 3

copeland 2015-02-04 20:40:26
3. You're so crazy!

acsigaoyuan 2015-02-04 20:40:53
none of them work

bobispro5 2015-02-04 20:40:53
we need the denominator to be 6

DrMath 2015-02-04 20:40:53
bad 3, everything should be <3

bobispro5 2015-02-04 20:40:53
we need denominator to be 6 in order to have sin(x) = 1/2

copeland 2015-02-04 20:40:57
We're trying to solve $\cos(a\pi)=\pm\sin(b\pi).$ Cosine and sine are hard to compare so it's better to write \[\cos(a\pi)=\pm\cos\left(\frac{\pi}2-b\pi\right)\]

copeland 2015-02-04 20:41:04
That happens when we can solve some equation with $a\pi,$ $b\pi,$ and $\frac\pi2.$ However if the denominator of $a$ is odd, we will need the denominator of $b$ to be twice that in order to solve the equation. By way of example:
\begin{align*}
\cos\left(\frac{1\pi}3\right)&=\sin\left(\frac{\pi}6\right)=\sin\left(\frac{5\pi}6\right)=-\sin\left(\frac{7\pi}6\right)=-\sin\left(\frac{11\pi}6\right)\\
\cos\left(\frac{3\pi}5\right)&=-\sin\left(\frac{\pi}{10}\right)=-\sin\left(\frac{9\pi}{10}\right)=\sin\left(\frac{11\pi}{10}\right)=\sin\left(\frac{19\pi}{10}\right)\\
\end{align*}

copeland 2015-02-04 20:41:25
So. . .

bli1999 2015-02-04 20:42:11
The sin can't be equal to the cosine

acsigaoyuan 2015-02-04 20:42:11
We can only try the cases where denominator is 4

copeland 2015-02-04 20:42:15
When the denominator of $a$ is an odd value $d$ we would need the denominator of $b$ to be $2d.$ Therefore we never enter case (C) when $d$ is 3 or 5.

acsigaoyuan 2015-02-04 20:42:29
denominator = 4 gives the last 16 cases

copeland 2015-02-04 20:42:37
All that is left is denominator 4. If $a\pi$ is an odd multiple of $\dfrac\pi4$ when are we in case (C), \[\cos(a\pi)=\pm\sin(b\pi)?\]

bobispro5 2015-02-04 20:42:58
16 cases

copeland 2015-02-04 20:43:02
How many of them work?

copeland 2015-02-04 20:44:41
That is, how many of our \[\cos\frac{u\pi}4=\pm\sin\frac{v\pi}4\] are true?

Studiosa 2015-02-04 20:44:53
all of them?

bobispro5 2015-02-04 20:44:53
all?

acsigaoyuan 2015-02-04 20:44:53
16, any combination works

cellobix 2015-02-04 20:44:53
All of them work.

Happytycho 2015-02-04 20:44:53
all 16?

Dukejukem 2015-02-04 20:44:53
$4 \times 4 = 16$ times

copeland 2015-02-04 20:44:59
In this instance everything is either $\pm\dfrac1{\sqrt2}.$ Now we pick up all of the pairs $(a\pi,b\pi)$ where either one is an odd multiple of $\dfrac\pi4.$

copeland 2015-02-04 20:45:02

copeland 2015-02-04 20:45:08
\[\begin{array}{c|c|c|c}
{a\pi}&\cos(a\pi)=0&\sin(b\pi)=0&\cos(a\pi)=\pm\sin(b\pi)\\
\hline
0\pi&&0\pi,1\pi&\frac\pi2,\frac{3\pi}2\\
1\pi&&0\pi,1\pi&\frac\pi2,\frac{3\pi}2\\
\hline
\frac12\pi&\text{all 20}&{\color{red}{0\pi,1\pi}}&{\color{red}{0\pi,1\pi}}\\
\frac32\pi&\text{all 20}&{\color{red}{0\pi,1\pi}}&{\color{red}{0\pi,1\pi}}\\
\hline
\frac13\pi&&0\pi,1\pi\\
\frac23\pi&&0\pi,1\pi\\
\frac43\pi&&0\pi,1\pi\\
\frac53\pi&&0\pi,1\pi\\
\hline
\frac14\pi&&0\pi,1\pi&\frac\pi4,\frac{3\pi}4,\frac{5\pi}4,\frac{7\pi}4\\
\frac34\pi&&0\pi,1\pi&\frac\pi4,\frac{3\pi}4,\frac{5\pi}4,\frac{7\pi}4\\
\frac54\pi&&0\pi,1\pi&\frac\pi4,\frac{3\pi}4,\frac{5\pi}4,\frac{7\pi}4\\
\frac74\pi&&0\pi,1\pi&\frac\pi4,\frac{3\pi}4,\frac{5\pi}4,\frac{7\pi}4\\
\hline
\frac15\pi&&0\pi,1\pi\\
\frac25\pi&&0\pi,1\pi\\
\frac35\pi&&0\pi,1\pi\\
\frac45\pi&&0\pi,1\pi\\
\frac65\pi&&0\pi,1\pi\\
\frac75\pi&&0\pi,1\pi\\
\frac85\pi&&0\pi,1\pi\\
\frac95\pi&&0\pi,1\pi\\
\hline
\text{new}&40&36&20\\
\end{array}\]

copeland 2015-02-04 20:45:11
And the answer?

Studiosa 2015-02-04 20:46:09
D

bobispro5 2015-02-04 20:46:09
96/400

acsigaoyuan 2015-02-04 20:46:09
D, 96/400 = 6/25

giftedbee 2015-02-04 20:46:09
96/400=6/25=D

bobispro5 2015-02-04 20:46:09
96/400 --> 6/25 (D)

briyellowduck 2015-02-04 20:46:09
D

mathwizard888 2015-02-04 20:46:09
D

MathStudent2002 2015-02-04 20:46:09
96/400=6/25 (D)

EulerMacaroni 2015-02-04 20:46:09
6/25

wehac 2015-02-04 20:46:09
96/400=6/25

briyellowduck 2015-02-04 20:46:09
6/25

spartan168 2015-02-04 20:46:09
D!

ompatel99 2015-02-04 20:46:51
How are we expected to solve this on test day with a time limit?

copeland 2015-02-04 20:46:53
No idea. This problem was a lot of work. The redeeming feature for me was that the distractors were all so bad that I knew when I made a mistake - the answer wasn't there!

copeland 2015-02-04 20:47:21
Sorry, by "bad" I mean there are so many ways to fail at this problem that making it multiple choice makes it much easier.

briyellowduck 2015-02-04 20:47:52
Now the biggest and baddest...

copeland 2015-02-04 20:47:53
Oh hey! We've got one more problem to go!

copeland 2015-02-04 20:48:09
Interestingly, I thought 24 was both biggest and baddest.

copeland 2015-02-04 20:48:15
25. A collection of circles in the upper half-plane, all tangent to the $x$-axis, is constructed in layers as follows. Layer $L_0$ consists of two circles of radii $70^2$ and $73^2$ that are externally tangent. For $k \ge 1,$ the circles in $\bigcup_{j=0}^{k-1} L_j$ are ordered according to their points of tangency with the $x$-axis. For every pair of consecutive circles in this order, a new circle is constructed externally tangent to each of the two circles in the pair. Layer $L_k$ consists of the $2^{k-1}$ circles constructed in this way. Let $S = \bigcup_{j=0}^6 L_j,$ and for every circle $C$ denote by $r(C)$ its radius. What is
\[
\sum_{C \in S} \frac{1}{\sqrt{r(C)}}\;?
\]
$\phantom{golly}$
(A) $\dfrac{286}{35}$ (B) $\dfrac{583}{70}$ (C) $\dfrac{715}{73}$ (D) $\dfrac{143}{14}$ (E) $\dfrac{1573}{146}$

cellobix 2015-02-04 20:48:36
...What?

copeland 2015-02-04 20:48:41
Yes. Words.

copeland 2015-02-04 20:48:48
Oh, I owe you a picture.

copeland 2015-02-04 20:48:50

copeland 2015-02-04 20:48:55
Looks complicated! Where can we start?

Dukejukem 2015-02-04 20:50:59
Descartes Circle Theorem?

mssmath 2015-02-04 20:50:59
Either Decartes or use Pythag

copeland 2015-02-04 20:51:02
This is an unfortunate thing about this problem. There's a theorem that gives us a shortcut.

copeland 2015-02-04 20:51:22
Let's figure out how to construct the new circles.

copeland 2015-02-04 20:51:24
Specifically, if we want to place a new circle between a circle of radius $r$ and a circle of radius $s$, how big should the new circle be?

copeland 2015-02-04 20:51:37
Here's a picture:

copeland 2015-02-04 20:51:39
How can we determine $t$ in terms of $r$ and $s$?

copeland 2015-02-04 20:51:42

Tuxianeer 2015-02-04 20:52:32
draw some center to center lines

hnkevin42 2015-02-04 20:52:32
pythagorean theorem?

Studiosa 2015-02-04 20:52:32
Draw triangles

ompatel99 2015-02-04 20:52:32
connect centers and pythag

Duncanyang 2015-02-04 20:52:32
pythagorean theorem

DivideBy0 2015-02-04 20:52:32
connect centers through tangent points

happyhummingbird 2015-02-04 20:52:32
pythagorean theoreom by connecting the radi

DivideBy0 2015-02-04 20:52:32
connect centers through tangent points and make pythag equations

EulerMacaroni 2015-02-04 20:52:37
Connect centers and apply the Pythagorean theorem

acsigaoyuan 2015-02-04 20:52:38
All I did is using simple pythagorean...

copeland 2015-02-04 20:52:40
Usually it's really helpful to connect the centers, so let's do that:

copeland 2015-02-04 20:52:44

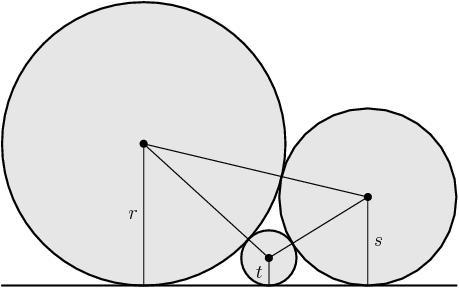
copeland 2015-02-04 20:52:44
It's also usually really helpful to create right triangles...

copeland 2015-02-04 20:52:45
So let's draw some horizontal lines to make right triangles:

copeland 2015-02-04 20:52:49

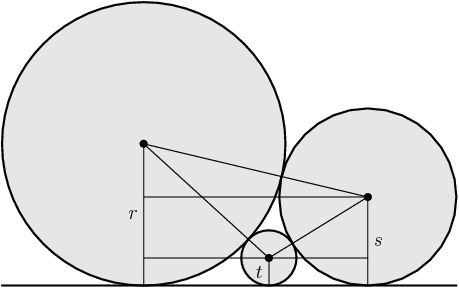
copeland 2015-02-04 20:52:53
What do we know about the blue triangle below?

copeland 2015-02-04 20:52:56

EulerMacaroni 2015-02-04 20:53:26
there is a right angle

prpaxson 2015-02-04 20:53:26
it is a right triangle

masad24 2015-02-04 20:53:26
its a right triangle

flyrain 2015-02-04 20:53:26
we know it's side lenghts

copeland 2015-02-04 20:53:27
And its dimensions?

bobispro5 2015-02-04 20:53:58
hypotenuse r+s, one leg r-s

mathmass 2015-02-04 20:53:58
r-s,r+s

jkyman 2015-02-04 20:53:58
hypotenuse is r + s

mathmass 2015-02-04 20:53:58
r-s

EulerMacaroni 2015-02-04 20:53:58
r-s, r+s

acsigaoyuan 2015-02-04 20:53:58
r+s, r-s and d where d is the length of the bottom line

pinkrock 2015-02-04 20:53:58
r+s is hypoteneuse

treemath 2015-02-04 20:53:58
hypotenuse = r+s and short leg = r-s

Studiosa 2015-02-04 20:53:58
hypotenuse r+s, leg r-s

copeland 2015-02-04 20:54:02
Its hypotenuse is $r+s$ and its left leg is $r-s$. So what is the horizontal leg?

bobispro5 2015-02-04 20:54:33
r+s, r-s, 2*sqrt(rs)

flyrain 2015-02-04 20:54:33
r-s, r+s, sqrt(4rs)

drywood 2015-02-04 20:54:33
r-s by r+s by 2sqrtrs

lucylai 2015-02-04 20:54:33
r+s,r-s,2sqrt(rs)

MathStudent2002 2015-02-04 20:54:33
2sqrt(rs)

drywood 2015-02-04 20:54:33
2sqrt(rs)

mrowhed 2015-02-04 20:54:33
2 sqrt(rs)

math_cool 2015-02-04 20:54:33
2(sqrt(rs))

MathStudent2002 2015-02-04 20:54:33
$2\sqrt{rs}$

wehac 2015-02-04 20:54:33
2sqrt(rs)

copeland 2015-02-04 20:54:35
It's $\sqrt{(r+s)^2 - (r-s)^2}.$

copeland 2015-02-04 20:54:37
This simplifies to just $2\sqrt{rs}.$

copeland 2015-02-04 20:54:39
Now, what about the two red triangles below?

copeland 2015-02-04 20:54:43

masad24 2015-02-04 20:55:14
they are right triangles too

Duncanyang 2015-02-04 20:55:14
they are right

prpaxson 2015-02-04 20:55:14
also right triangles

Happytycho 2015-02-04 20:55:17
also right triangles

copeland 2015-02-04 20:55:19
What else are they, now that we're talking similarities?

copeland 2015-02-04 20:56:16
(They are not 'similar.' That was not a hint at something.)

drywood 2015-02-04 20:56:46
they have horizontal sides of length 2sqrt(rt) and 2sqrt(st)

Studiosa 2015-02-04 20:56:46
same process for hypotenuse and short leg

Studiosa 2015-02-04 20:56:46
r+t and s+t for the hypotenuses, r-t and s-t for legs

az_phx_brandon_jiang 2015-02-04 20:56:46
also r-t and r+t, s-t and s+t

Dukejukem 2015-02-04 20:56:57
"Double-counting," we find that \[2\sqrt{rs} = \sqrt{\left(s + t\right)^2 - \left(s - t\right)^2} + \sqrt{\left(r + t\right)^2 - \left(r - t\right)^2}\]\[= 2\sqrt{st} + 2\sqrt{rt}\]

acsigaoyuan 2015-02-04 20:56:59
On left: hypotenuse r+t, left leg r-t, horizontal leg 2*sqrt(rt)

copeland 2015-02-04 20:57:02
By the same reasoning, the horizontal leg of the left triangle is $2\sqrt{rt}$, and the horizontal leg of the right triangle is $2\sqrt{st}.$

copeland 2015-02-04 20:57:13
Since the blue horizontal leg must equal the sum of the two red ones, we have
\[
2\sqrt{rs} = 2\sqrt{rt} + 2\sqrt{st}.
\]

copeland 2015-02-04 20:57:30
We could solve this for $t$, but what's a better idea?

lucylai 2015-02-04 20:58:21
divide by 2sqrt(rst)

mrowhed 2015-02-04 20:58:21
divide by 2 sqrt(rst)

awesomemathlete 2015-02-04 20:58:21
divide by $2\sqrt{rst}$

TheMaskedMagician 2015-02-04 20:58:21

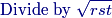
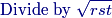
ashgabat 2015-02-04 20:58:21
Divide everything by sqrt(r*s*t)/2

copeland 2015-02-04 20:58:25
Let's make it a bit nicer by dividing through by $2\sqrt{rst}.$ This gives us
\[
\frac{1}{\sqrt{t}} = \frac{1}{\sqrt{s}} + \frac{1}{\sqrt{r}}.
\]

copeland 2015-02-04 20:58:39
Are we on the right track?

ashgabat 2015-02-04 20:59:02
It's of the form we want in the answer

Dukejukem 2015-02-04 20:59:02
Aha! this looks like the obscure sum we're supposed to calculate

kingsave3166 2015-02-04 20:59:02
yeah we have reciprocals in the question

MathStudent2002 2015-02-04 20:59:02
Hey look $\dfrac{1}{\sqrt{t}}$ is part of our answer!

TheMaskedMagician 2015-02-04 20:59:02
Says we see reciprocals of radicals in the desired sum

copeland 2015-02-04 20:59:06
Aha! These are the same terms that we have in the sum that we want to compute: reciprocals of square roots of radii!

copeland 2015-02-04 20:59:10
Now what?

acsigaoyuan 2015-02-04 20:59:54
find L1, L2, ...

codyj 2015-02-04 20:59:54
small cases

prpaxson 2015-02-04 20:59:54
plug in the ones given, 70^2 and 73^2

Tuxianeer 2015-02-04 20:59:54
start with 70^2 and 73^2

TheMaskedMagician 2015-02-04 20:59:54
Find the sum for each layer in terms of $L_0$

ompatel99 2015-02-04 20:59:54
use layer L0

pinkrock 2015-02-04 20:59:54
create series

copeland 2015-02-04 20:59:56
Now we have to keep track of the sums of these things, so let's name them.

copeland 2015-02-04 21:00:03
Let's set $R_k$ to be the sum of these terms for the circles in level $k$, and let's set $S_k$ to be the sum of these terms for all the levels 0 up through $k$. So what we want to compute is $S_6 = R_0 + R_1 + R_2 + \cdots + R_6.$

copeland 2015-02-04 21:00:14
Also, so we don't have to carry all the numbers around, let's set $a = \dfrac{1}{70}$ and $b = \dfrac{1}{73}$. Then $R_0 = S_0 = a+b.$

copeland 2015-02-04 21:00:23
How do we compute $R_k?$

acsigyz 2015-02-04 21:00:42
very carefully

giftedbee 2015-02-04 21:00:42
Recursively!

copeland 2015-02-04 21:00:44
Alright!

copeland 2015-02-04 21:00:53
So, recursion. . .

pinkrock 2015-02-04 21:01:27
use the previous levels and the formula we found

copeland 2015-02-04 21:01:29
How can we use those?

copeland 2015-02-04 21:02:21
What does our formula tell us about the sum of the reciprocals of all the circles in $L_k?$

Dukejukem 2015-02-04 21:02:58
Note that every circle $O$ in the $k$th layer is constructed from two circles in the $k -1$th layer. Hence, Rk=2Rk−1

copeland 2015-02-04 21:03:01
This is close.

copeland 2015-02-04 21:03:16
Every circle is 'made from' circles in the previous layers.

copeland 2015-02-04 21:04:16
Except $R_k$ counts just the current layer. What do we really count from before when constructing?

copeland 2015-02-04 21:04:31
Here's our picture again:

copeland 2015-02-04 21:04:32

copeland 2015-02-04 21:04:52
Layer 1 has 1 circle. Layer 2 has 2 and Layer 4 has 4.

copeland 2015-02-04 21:05:10
How many circles do I need to use to construct Layer 4?

copeland 2015-02-04 21:05:15
(Layer 0 also has 2.)

acsigaoyuan 2015-02-04 21:06:02
We count all existing circles?

kingsave3166 2015-02-04 21:06:02
layer 4 needs 8

briyellowduck 2015-02-04 21:06:02
8

copeland 2015-02-04 21:06:03
5 and 8 are both good answers. I need ALL 5 of the previous circles. I count some of them twice so with multiplicity I need 8.

copeland 2015-02-04 21:06:09
Which ones do I count once?

Tuxianeer 2015-02-04 21:06:59
70^2 and 73^2

az_phx_brandon_jiang 2015-02-04 21:06:59
The outer original two

acsigaoyuan 2015-02-04 21:06:59
the two on L0

kingsave3166 2015-02-04 21:06:59
70 and 73

Studiosa 2015-02-04 21:06:59
The ones on the outside ends

copeland 2015-02-04 21:07:03
I count the ends once. Just for creating the first and last circles.

copeland 2015-02-04 21:07:08
And which ones do I count twice?

lucylai 2015-02-04 21:07:36
everything else

acsigaoyuan 2015-02-04 21:07:36
all the rest

Studiosa 2015-02-04 21:07:36
The smaller ones on the inside

math_cool 2015-02-04 21:07:36
Everything other circle

eswa2000 2015-02-04 21:07:36
the middle ones

DivideBy0 2015-02-04 21:07:36
all the ones in the middle

kingsave3166 2015-02-04 21:07:36
the ones we made in the prev layer

owm 2015-02-04 21:07:36
all of the others

copeland 2015-02-04 21:07:39
All the rest!

copeland 2015-02-04 21:07:52
Using our formula, it's the sum of these "reciprocal of square root" terms for all the circles that we already have in the lower levels.

copeland 2015-02-04 21:07:53
And each circle we already have is counted twice...

copeland 2015-02-04 21:07:55
...except for the two big circles on the ends, which only get counted once.

copeland 2015-02-04 21:08:24
The sum of the reciprocals for all the layers up to $k$ is $S_k.$

copeland 2015-02-04 21:08:35
The sum of the reciprocals on just layer $k$ is $R_k.$

copeland 2015-02-04 21:08:47
What recursive formula should we get for $R_k?$

Dukejukem 2015-02-04 21:10:04
Ok, so $R_k = R_0 + 2\left(R_1 + R_2 + ... + R_{k - 1}\right)$?

lucylai 2015-02-04 21:10:04
R_k=2S_k-R_0

acsigaoyuan 2015-02-04 21:10:04
R_k=2S_k-a-b

Dukejukem 2015-02-04 21:10:04
Ok, so \[R_k = R_0 + 2\left(R_1 + R_2 + ... + R_{k - 1}\right) = 2S_{k - 1} - R_0\]?

pinkrock 2015-02-04 21:10:04
Rk = 2Sk-(1/rt70 + 1/rt73)

copeland 2015-02-04 21:10:07
Great.

copeland 2015-02-04 21:10:13
We have $R_k = 2S_{k-1} - a - b.$

copeland 2015-02-04 21:10:18
And what does that give us for $S_k$?

lucylai 2015-02-04 21:11:32
S_k=3S_(k-1)-R_0

giftedbee 2015-02-04 21:11:32
3S_K-1 -a-b

kingsave3166 2015-02-04 21:11:32
S_k = 3s_(k-1)-a-b?

acsigaoyuan 2015-02-04 21:11:32
S_k = 3*S_k-1 - a - b

copeland 2015-02-04 21:11:35
$S_k = R_k + S_{k-1} = 3S_{k-1} - a - b.$

copeland 2015-02-04 21:12:02
Since $a+b=R_0$ we now have the simple recurrence $S_0 = R_0$ and $S_k = 3S_{k-1} - R_0.$

copeland 2015-02-04 21:12:09
What does that ALMOST look like?

cellobix 2015-02-04 21:13:21
Geometric sequence

lucylai 2015-02-04 21:13:21
S_k=3^k*R_0

va2010 2015-02-04 21:13:21
powers of 3!

zacchro 2015-02-04 21:13:21
powers of three recurrence?

copeland 2015-02-04 21:13:23
That is almost geometric. Can we do something to make it geometric?

copeland 2015-02-04 21:14:23
Can you see a way to make the right side a third of the left side?

cellobix 2015-02-04 21:15:32
Subtract (R_0)/2 from both sides

giftedbee 2015-02-04 21:15:32
Do a new Sk=Sk-(a-b)/2

lucylai 2015-02-04 21:15:32
subtract R_0/2 from both sides

kingsave3166 2015-02-04 21:15:32
subtract r_0 / 2 from both sides

copeland 2015-02-04 21:15:40
It's almost exponential. We can make it exponential by subtracting $\dfrac{R_0}2$:\[S_k-\dfrac{R_0}2=3\left(S_{k-1}-\dfrac{R_0}2\right).\]

copeland 2015-02-04 21:15:50
(Cool, huh?)

copeland 2015-02-04 21:15:53
Going down the chain we get \[S_k-\dfrac{R_0}2=3^k\left(S_{0}-\dfrac{R_0}2\right)=\dfrac{3^k R_0}2.\]or\[S_k=\dfrac{(3^k+1) R_0}2.\]

copeland 2015-02-04 21:16:10
So our answer is $\dfrac{(729+1)}2\left(\dfrac{1}{70} + \dfrac{1}{73}\right).$

copeland 2015-02-04 21:16:42
Want me to do the arithmetic?

giftedbee 2015-02-04 21:16:55
365*143/70*73=143/14=D

mrowhed 2015-02-04 21:16:55
yea

prpaxson 2015-02-04 21:16:55
yes

treemath 2015-02-04 21:16:55
sure

kingsave3166 2015-02-04 21:16:55
yes please

acsigaoyuan 2015-02-04 21:16:55
143/14!

Jayjayliu 2015-02-04 21:16:55
do it

bobispro5 2015-02-04 21:16:55
lol its nice

treemath 2015-02-04 21:16:55
please doooooooooooo

pinkrock 2015-02-04 21:16:55
yes please

copeland 2015-02-04 21:16:58
This simplifies to $\dfrac{73}{14} + 5 = \dfrac{143}{14}.$ Answer (D).

copeland 2015-02-04 21:17:18
If you don't see that exponential thing right away you could just grind through the recursion directly.

copeland 2015-02-04 21:17:40
If you write $c=R_0,$ the recursion looks something like:

copeland 2015-02-04 21:17:44
\begin{align*}
S_0 &= c \\
S_1 &= 3S_0 - c = 2c \\
S_2 &= 3S_1 - c = 5c \\
S_3 &= 3S_2 - c = 14c \\
S_4 &= 3S_3 - c = 41c \\
S_5 &= 3S_4 - c = 122c \\
S_6 &= 3S_5 - c = 365c
\end{align*}

copeland 2015-02-04 21:17:56
So our answer is again $365c = 365\left(\dfrac{1}{70} + \dfrac{1}{73}\right).$

Tuxianeer 2015-02-04 21:18:35
unfortunately 143=70+73 so it seems more easily guessable than would be best

copeland 2015-02-04 21:18:42
Yeah, that's wild.

copeland 2015-02-04 21:19:15
It's clear the numerator has to have a factor of 143. It would be nice if they could have picked a more obscure sum. . .

Duncanyang 2015-02-04 21:19:37
what if this process were to be continued indefinitely

copeland 2015-02-04 21:19:45
It's infinte. Our sum is like $3^k.$

copeland 2015-02-04 21:21:24
Alright, that's all for tonight's Math Jam!

copeland 2015-02-04 21:21:27
Please join us again on Thursday, February 26, when we will discuss the AMC 10B/12B contests and also again on March 21 and 27 when we will be discussing the AIME I and II contests.

copeland 2015-02-04 21:21:39
Oh, and you can find videos for the last 5 problems of each exam on the videos page:
http://www.artofproblemsolving.com/Videos/index.php?type=amc
I believe that Richard chose some different tactics in his videos than we used today, so it might be worth checking them out.

GU35T-31415 2015-02-04 21:21:53
Thank you!

catfishie6 2015-02-04 21:21:53
Thanks!

acsigaoyuan 2015-02-04 21:21:53
Thank you!

Studiosa 2015-02-04 21:21:53
Thank you!

copeland 2015-02-04 21:21:55
Thank you guys, too.

copeland 2015-02-04 21:22:15
You can find discussions of all these problems on our forums and you can find solutions in the contests section of the site.

2015 AMC 10/12 A Discussion

Facilitator: Jeremy Copeland