2015 AMC 10/12 B Discussion
Go back to the Math Jam ArchiveA discussion of problems from the AMC 10/12 B, which is administered February 25. We will cover the last 5 problems on each test, as well as requested earlier problems on the tests.
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.
Facilitator: Dave Patrick
DPatrick
2015-02-26 19:00:13
Welcome to the 2015 AMC 10B/12B Math Jam!
Welcome to the 2015 AMC 10B/12B Math Jam!
DPatrick
2015-02-26 19:00:19
I'm Dave Patrick, and I'll be leading our discussion tonight.
I'm Dave Patrick, and I'll be leading our discussion tonight.
DPatrick
2015-02-26 19:00:27
Before we get started I would like to take a moment to explain our virtual classroom procedures to those who have not previously participated in a Math Jam or one of our online classes.
Before we get started I would like to take a moment to explain our virtual classroom procedures to those who have not previously participated in a Math Jam or one of our online classes.
DPatrick
2015-02-26 19:00:34
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
DPatrick
2015-02-26 19:00:52
There are a lot of students here! (Over 200 so far and counting.) As I said, only (a fraction of the) well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
There are a lot of students here! (Over 200 so far and counting.) As I said, only (a fraction of the) well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
DPatrick
2015-02-26 19:01:13
Also, we won't always be going through the math quite as thoroughly as we do in our classes -- I can't teach all the prerequisite material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!
Also, we won't always be going through the math quite as thoroughly as we do in our classes -- I can't teach all the prerequisite material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!
DPatrick
2015-02-26 19:01:23
We have 2 assistants tonight helping out: Jackie (3628800J) and Ray Kim (crescendo).
We have 2 assistants tonight helping out: Jackie (3628800J) and Ray Kim (crescendo).
DPatrick
2015-02-26 19:01:28
Jackie lives in Michigan, where she won the statewide Michigan Math Prize Competition. She was also a 3-time USA(J)MO qualifier and a member of the USA team at the International Linguistics Olympiad. She plans to major in math and computer science.
Jackie lives in Michigan, where she won the statewide Michigan Math Prize Competition. She was also a 3-time USA(J)MO qualifier and a member of the USA team at the International Linguistics Olympiad. She plans to major in math and computer science.
DPatrick
2015-02-26 19:01:39
Ray is currently attending UNC Chapel Hill as an undergrad, looking to get a degree in math and computer science. His hometown is Asheville, NC, and while he was there he took numerous AoPS classes throughout his middle and early high school career which really boosted his understanding of math and other topics that don't get covered in the regular school curriculum.
Ray is currently attending UNC Chapel Hill as an undergrad, looking to get a degree in math and computer science. His hometown is Asheville, NC, and while he was there he took numerous AoPS classes throughout his middle and early high school career which really boosted his understanding of math and other topics that don't get covered in the regular school curriculum.
DPatrick
2015-02-26 19:01:54
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the incredibly large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the incredibly large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.
DPatrick
2015-02-26 19:02:10
Please also remember that the purpose of this Math Jam is to work through the solutions to AMC problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be posted.
Please also remember that the purpose of this Math Jam is to work through the solutions to AMC problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be posted.
DPatrick
2015-02-26 19:02:25
We will work the last 5 problems from the AMC 10B, then the last 5 problems from the AMC 12B. Two pairs of these problems are the same, 10B and 12B have the same Problem 21 and 10B Problem 25 is 12B Problem 23. We'll only solve those problems once.
We will work the last 5 problems from the AMC 10B, then the last 5 problems from the AMC 12B. Two pairs of these problems are the same, 10B and 12B have the same Problem 21 and 10B Problem 25 is 12B Problem 23. We'll only solve those problems once.
DPatrick
2015-02-26 19:02:36
After that, time permitting, we may do another problem or two. We'll run for about 2 hours.
After that, time permitting, we may do another problem or two. We'll run for about 2 hours.
DPatrick
2015-02-26 19:02:52
Let's get started!
Let's get started!
DPatrick
2015-02-26 19:02:58
#21 was the same on both contests:
#21 was the same on both contests:
DPatrick
2015-02-26 19:03:03
21. Cozy the Cat and Dash the Dog are going up a staircase with a certain number of steps. However, instead of walking up the steps one at a time, both Cozy and Dash jump. Cozy goes two steps up with each jump (though if necessary, he will just jump the last step). Dash goes five steps up with each jump (though if necessary, he will just jump the last steps if there are fewer than 5 steps left). Suppose that Dash takes 19 fewer jumps than Cozy to reach the top of the staircase. Let s denote the sum of all possible numbers of steps this staircase can have. What is the sum of the digits of s?
10B:21
(A) 9(B) 11(C) 12(D) 13(E) 15
21. Cozy the Cat and Dash the Dog are going up a staircase with a certain number of steps. However, instead of walking up the steps one at a time, both Cozy and Dash jump. Cozy goes two steps up with each jump (though if necessary, he will just jump the last step). Dash goes five steps up with each jump (though if necessary, he will just jump the last steps if there are fewer than 5 steps left). Suppose that Dash takes 19 fewer jumps than Cozy to reach the top of the staircase. Let s denote the sum of all possible numbers of steps this staircase can have. What is the sum of the digits of s?
10B:21
(A) 9(B) 11(C) 12(D) 13(E) 15
WhaleVomit
2015-02-26 19:03:32
use ceiling functions
use ceiling functions
Deathranger999
2015-02-26 19:03:32
We can set up an equation with ceiling function.
We can set up an equation with ceiling function.
BFYSharks
2015-02-26 19:03:32
Ceiling function
Ceiling function
thkim1011
2015-02-26 19:03:32
let's write an equation with ceiling functions
let's write an equation with ceiling functions
DPatrick
2015-02-26 19:03:57
We could certainly use the ceiling function, but I think it's perhaps even clearer if we don't.
We could certainly use the ceiling function, but I think it's perhaps even clearer if we don't.
stan23456
2015-02-26 19:04:28
set up cases
set up cases
DPatrick
2015-02-26 19:04:38
That's sort of what I did. Let's suppose Dash takes n+1 steps to climb the staircase: n regular steps plus a final step of size d, where 1≤d≤5.
That's sort of what I did. Let's suppose Dash takes n+1 steps to climb the staircase: n regular steps plus a final step of size d, where 1≤d≤5.
DPatrick
2015-02-26 19:04:49
Then how big is the staircase?
Then how big is the staircase?
ninjataco
2015-02-26 19:05:05
5n+d
5n+d
AMN300
2015-02-26 19:05:05
5n+d
5n+d
abean077
2015-02-26 19:05:05
5n + d steps
5n + d steps
swirlykick
2015-02-26 19:05:05
5n+d
5n+d
speck
2015-02-26 19:05:05
Steps = 5n+ d
Steps = 5n+ d
MathLearner01
2015-02-26 19:05:05
5n+d
5n+d
_--__--_
2015-02-26 19:05:05
5n + d steps
5n + d steps
geogirl08
2015-02-26 19:05:05
5n + d
5n + d
DPatrick
2015-02-26 19:05:09
Each regular step is 5 stairs, so Dash's total is 5n+d.
Each regular step is 5 stairs, so Dash's total is 5n+d.
DPatrick
2015-02-26 19:05:15
How about Cozy the Cat?
How about Cozy the Cat?
DPatrick
2015-02-26 19:05:35
If Dash takes n regular steps, how many regular steps does Cozy take?
If Dash takes n regular steps, how many regular steps does Cozy take?
AMN300
2015-02-26 19:05:47
n+19
n+19
Tommy2000
2015-02-26 19:05:47
n+19
n+19
mishka1980
2015-02-26 19:05:47
(n+19)
(n+19)
DPatrick
2015-02-26 19:05:51
Right, Cozy takes 19+n regular steps and a final step of size c, where 1≤c≤2.
Right, Cozy takes 19+n regular steps and a final step of size c, where 1≤c≤2.
DPatrick
2015-02-26 19:06:05
So what's the size of the staircase using these variables?
So what's the size of the staircase using these variables?
SimonSun
2015-02-26 19:06:19
38+2n+c
38+2n+c
swirlykick
2015-02-26 19:06:19
2n+38+c
2n+38+c
LOTRFan123
2015-02-26 19:06:19
2n+38+c
2n+38+c
AMN300
2015-02-26 19:06:19
2(n+19)+c
2(n+19)+c
WalkerTesla
2015-02-26 19:06:19
38+2n+c
38+2n+c
bellyflop
2015-02-26 19:06:19
2n + 38 + c
2n + 38 + c
DPatrick
2015-02-26 19:06:24
Right: Cozy's total steps is 2(19+n)+c.
Right: Cozy's total steps is 2(19+n)+c.
DPatrick
2015-02-26 19:06:30
But Dash and Cozy climb the same staircase!
But Dash and Cozy climb the same staircase!
DPatrick
2015-02-26 19:06:36
So we have the equation
5n+d=2(19+n)+c.
So we have the equation
5n+d=2(19+n)+c.
AMN300
2015-02-26 19:07:05
3n = 38+(c-d) and casework from here
3n = 38+(c-d) and casework from here
geogirl08
2015-02-26 19:07:05
solve for n?
solve for n?
bestwillcui1
2015-02-26 19:07:05
3n=38+c-d then solve
3n=38+c-d then solve
Darn
2015-02-26 19:07:05
Rearrange the variables
Rearrange the variables
DPatrick
2015-02-26 19:07:11
Exactly: let's solve for n:
3n=38−d+c.
Exactly: let's solve for n:
3n=38−d+c.
DPatrick
2015-02-26 19:07:16
What do we know about −d+c?
What do we know about −d+c?
lucylai
2015-02-26 19:07:57
1 mod 3
1 mod 3
MathLearner01
2015-02-26 19:08:19
1 mod 3
1 mod 3
mihirb
2015-02-26 19:08:19
which is 1 mod 3
which is 1 mod 3
Benaloo26
2015-02-26 19:08:25
greater or equal to -4, less than or equal to 1
greater or equal to -4, less than or equal to 1
nosyarg
2015-02-26 19:08:25
it can be from -4 to 1
it can be from -4 to 1
Tommy2000
2015-02-26 19:08:25
Ranges from -4 to 1
Ranges from -4 to 1
DPatrick
2015-02-26 19:08:31
Yes. d is between 1 and 5 (inclusive), and c is either 1 or 2. So −d+c is an integer between 1 and -4 (inclusive).
Yes. d is between 1 and 5 (inclusive), and c is either 1 or 2. So −d+c is an integer between 1 and -4 (inclusive).
DPatrick
2015-02-26 19:08:50
But also, since 3n=38−d+c, we must have that 38−d+c is a multiple of 3. This means that −d+c must be 1 or -2 --- those are the only numbers in our range that produce a multiple of 3.
But also, since 3n=38−d+c, we must have that 38−d+c is a multiple of 3. This means that −d+c must be 1 or -2 --- those are the only numbers in our range that produce a multiple of 3.
DPatrick
2015-02-26 19:09:03
(In shorthand, −d+c must be equivalent to 1 mod 3.)
(In shorthand, −d+c must be equivalent to 1 mod 3.)
Eugenis
2015-02-26 19:09:10
So we just check all the cases from there
So we just check all the cases from there
DPatrick
2015-02-26 19:09:25
Right. We just check the two cases −d+c=1 and −d+c=−2 and list the possibilities.
Right. We just check the two cases −d+c=1 and −d+c=−2 and list the possibilities.
DPatrick
2015-02-26 19:09:33
If −d+c=1, what do we know?
If −d+c=1, what do we know?
TheMagician
2015-02-26 19:10:00
n=13
n=13
kunsun
2015-02-26 19:10:00
n = 13
n = 13
TheMaskedMagician
2015-02-26 19:10:00


WhaleVomit
2015-02-26 19:10:00
n=13
n=13
nosaj
2015-02-26 19:10:00
n=13
n=13
amburger66
2015-02-26 19:10:00
d=1, c=2
d=1, c=2
ompatel99
2015-02-26 19:10:00
c=2,d=1
c=2,d=1
jam10307
2015-02-26 19:10:00
d=1, c=2
d=1, c=2
DPatrick
2015-02-26 19:10:04
We must have (d,c)=(1,2) for this to happen.
We must have (d,c)=(1,2) for this to happen.
DPatrick
2015-02-26 19:10:10
We get 3n=39, so n=13. This means there are 5n+d=5(13)+1=66 stairs.
We get 3n=39, so n=13. This means there are 5n+d=5(13)+1=66 stairs.
DPatrick
2015-02-26 19:10:22
(As a check, you can verify that 2(n+19)+c=2(13+19)+2=2(32)+2=66 is the number of steps that Cozy climbs.)
(As a check, you can verify that 2(n+19)+c=2(13+19)+2=2(32)+2=66 is the number of steps that Cozy climbs.)
mihirb
2015-02-26 19:10:45
then we solve for n and d in the other case?
then we solve for n and d in the other case?
DPatrick
2015-02-26 19:10:51
In the other case we have −d+c=−2. This gives 3n=38−2=36, so n=12. What are the possibilities?
In the other case we have −d+c=−2. This gives 3n=38−2=36, so n=12. What are the possibilities?
ompatel99
2015-02-26 19:11:13
(d,c)=(4,2) and (3,1) for -d+c=-2
(d,c)=(4,2) and (3,1) for -d+c=-2
Richardq
2015-02-26 19:11:13
(3,1) (4,2)
(3,1) (4,2)
abean077
2015-02-26 19:11:13
d = 4 c = 2, d = 3 c = 1
d = 4 c = 2, d = 3 c = 1
_--__--_
2015-02-26 19:11:13
c = 1 and d = 3, or c = 2 and d = 4
c = 1 and d = 3, or c = 2 and d = 4
DPatrick
2015-02-26 19:11:17
We can have (d,c) equal to (3,1) or to (4,2).
We can have (d,c) equal to (3,1) or to (4,2).
DPatrick
2015-02-26 19:11:27
If d=3, then 5n+d=5(12)+3=63 stairs are climbed.
If d=3, then 5n+d=5(12)+3=63 stairs are climbed.
DPatrick
2015-02-26 19:11:41
If d=4, then 5n+d=5(12)+4=64 stairs are climbed.
If d=4, then 5n+d=5(12)+4=64 stairs are climbed.
DPatrick
2015-02-26 19:11:48
So how do we finish?
So how do we finish?
Deathranger999
2015-02-26 19:12:05
Add them.
Add them.
ninjataco
2015-02-26 19:12:05
66+64+63=193, so the answer is 13 (D)
66+64+63=193, so the answer is 13 (D)
MinsPar
2015-02-26 19:12:05
s = 66+63+64
s = 66+63+64
Imagineny1
2015-02-26 19:12:05
add 63 64 66
add 63 64 66
acegikmoqsuwy2000
2015-02-26 19:12:05
so 193 total => 1+9+3=13
so 193 total => 1+9+3=13
mathperson9
2015-02-26 19:12:05
63+66+64= 193
63+66+64= 193
DPatrick
2015-02-26 19:12:09
The possible numbers of stairs are 63, 64, or 66. These sum to 193. The sum of the digits is 1+9+3=13. Answer (D).
The possible numbers of stairs are 63, 64, or 66. These sum to 193. The sum of the digits is 1+9+3=13. Answer (D).
DPatrick
2015-02-26 19:12:37
You could certainly have done this problem by trial-and-error, but the algebraic approach ensures that we catch all the solutions.
You could certainly have done this problem by trial-and-error, but the algebraic approach ensures that we catch all the solutions.
DPatrick
2015-02-26 19:12:46
On to 10B #22:
On to 10B #22:
DPatrick
2015-02-26 19:12:51
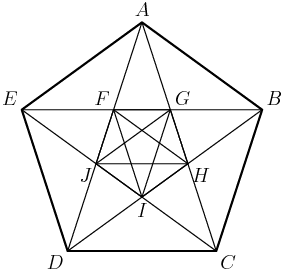
22. In the figure shown below, ABCDE is a regular pentagon and AG=1. What is FG+JH+CD?
10B:22
(A) 3(B) 12−4√5(C) 5+2√53(D) 1+√5(E) 11+11√510
22. In the figure shown below, ABCDE is a regular pentagon and AG=1. What is FG+JH+CD?
10B:22
(A) 3(B) 12−4√5(C) 5+2√53(D) 1+√5(E) 11+11√510
DPatrick
2015-02-26 19:12:57

bluephoenix
2015-02-26 19:13:20
Similar triangles!
Similar triangles!
InLhings
2015-02-26 19:13:20
Similar Triangles?
Similar Triangles?
math-rules
2015-02-26 19:13:20
Similar Triangles!!!
Similar Triangles!!!
BFYSharks
2015-02-26 19:13:20
Everything is isoceles!
Everything is isoceles!
Richardq
2015-02-26 19:13:20
Similar triangles?
Similar triangles?
abean077
2015-02-26 19:13:20
Similar triangles?
Similar triangles?
DivideBy0
2015-02-26 19:13:20
similar triangles with common vertex at A
similar triangles with common vertex at A
nosyarg
2015-02-26 19:13:20
similar triangles?
similar triangles?
DPatrick
2015-02-26 19:13:43
There are a gazillion similar isosceles triangles in this picture. (That'd be a fun problem too -- counting how many there are!)
There are a gazillion similar isosceles triangles in this picture. (That'd be a fun problem too -- counting how many there are!)
DPatrick
2015-02-26 19:13:53
Just so we have some notation to work with:
Just so we have some notation to work with:
DPatrick
2015-02-26 19:13:56
Let's set r to be a side of the big pentagon (so AB=r) and s to be a side of the small pentagon (so FG=s).
Let's set r to be a side of the big pentagon (so AB=r) and s to be a side of the small pentagon (so FG=s).
DPatrick
2015-02-26 19:14:03
How can we relate r and s?
How can we relate r and s?
numbertheory
2015-02-26 19:14:44
s = r-1
s = r-1
DPatrick
2015-02-26 19:15:07
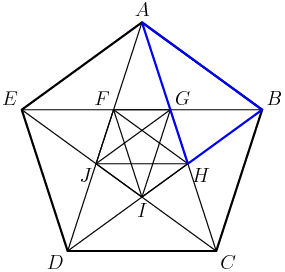
There are lots and lots of ways to proceed, but that's how I started. We can look at triangle ABH:
There are lots and lots of ways to proceed, but that's how I started. We can look at triangle ABH:
DPatrick
2015-02-26 19:15:13

akim99
2015-02-26 19:15:49
Isoceles!
Isoceles!
DPatrick
2015-02-26 19:15:51
Would you believe that triangle ABH is isosceles?
Would you believe that triangle ABH is isosceles?
DPatrick
2015-02-26 19:15:58
It looks "obvious" from the picture...but you can see it more rigorously too if you note that it's similar to triangle CHI, which is isosceles by symmetry.
It looks "obvious" from the picture...but you can see it more rigorously too if you note that it's similar to triangle CHI, which is isosceles by symmetry.
ingridzhang97
2015-02-26 19:16:22
its a 36 72 72 triangle
its a 36 72 72 triangle
zheyu1
2015-02-26 19:16:22
both 72 degree base angles
both 72 degree base angles
mathperson9
2015-02-26 19:16:22
You can solve for the angles
You can solve for the angles
DPatrick
2015-02-26 19:16:30
So since AH=AB, we have 1+s=r.
So since AH=AB, we have 1+s=r.
DPatrick
2015-02-26 19:16:54
And as many of you suggested earlier, there are lots of other ways to relate r and s too.
And as many of you suggested earlier, there are lots of other ways to relate r and s too.
BFYSharks
2015-02-26 19:17:03
Then similar triangles using AFG and ADC
Then similar triangles using AFG and ADC
akim99
2015-02-26 19:17:09
AF:AD = FG C
C
AF:AD = FG
DPatrick
2015-02-26 19:17:23
I like this too: I found it easiest to look at similar triangles AFG and ADC.
I like this too: I found it easiest to look at similar triangles AFG and ADC.
DPatrick
2015-02-26 19:17:29


DPatrick
2015-02-26 19:17:44
AFG has base s and legs of length 1.
ADC has base r and legs of length 2+s.
AFG has base s and legs of length 1.
ADC has base r and legs of length 2+s.
DPatrick
2015-02-26 19:17:57
So s=r2+s, and hence r=s(2+s).
So s=r2+s, and hence r=s(2+s).
TheMaskedMagician
2015-02-26 19:18:13


DPatrick
2015-02-26 19:18:21
Exactly: earlier we had r=1+s, so now we've got the equation 1+s=s(s+2) just in terms of s.
Exactly: earlier we had r=1+s, so now we've got the equation 1+s=s(s+2) just in terms of s.
DPatrick
2015-02-26 19:18:31
This simplifies to s2+s−1=0. So what is s?
This simplifies to s2+s−1=0. So what is s?
ninjataco
2015-02-26 19:18:53
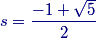
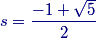
_--__--_
2015-02-26 19:18:53
quadratic formula
quadratic formula
TheMaskedMagician
2015-02-26 19:18:53
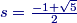
ompatel99
2015-02-26 19:18:53
(-1+sqrt(5))/2
(-1+sqrt(5))/2
MathStudent2002
2015-02-26 19:18:53
s=−1+√52
s=−1+√52
DPatrick
2015-02-26 19:18:57
By the quadratic formula,
s=−1±√52,
and since s>0, we must have s=√5−12.
By the quadratic formula,
s=−1±√52,
and since s>0, we must have s=√5−12.
DPatrick
2015-02-26 19:19:08
How do we finish from here?
How do we finish from here?
abean077
2015-02-26 19:19:32
figure out JH
figure out JH
Not_a_Username
2015-02-26 19:19:47
JH=1
JH=1
123456789agarwal
2015-02-26 19:19:47
JH =1
JH =1
ScottBusche
2015-02-26 19:19:47
Use ADC and AJH to find JH.
Use ADC and AJH to find JH.
DPatrick
2015-02-26 19:19:51
Right. We want FG+JH+CD, so we can use the three similar triangles shown in red below:
Right. We want FG+JH+CD, so we can use the three similar triangles shown in red below:
DPatrick
2015-02-26 19:19:57


DPatrick
2015-02-26 19:20:10
The top triangle AFG has legs of length 1 and a base of length s.
The top triangle AFG has legs of length 1 and a base of length s.
AMN300
2015-02-26 19:20:20
similar triangles, s*(s+1)
similar triangles, s*(s+1)
DPatrick
2015-02-26 19:20:28
Right, AJH has legs of length 1+s, so by similarity its base is s(1+s).
Right, AJH has legs of length 1+s, so by similarity its base is s(1+s).
vstar99
2015-02-26 19:20:57
so s+s^2
so s+s^2
DPatrick
2015-02-26 19:21:01
Yes, and at this point, you might recall that s2+s−1=0, so s(1+s) is just 1. That is, JH=1.
Yes, and at this point, you might recall that s2+s−1=0, so s(1+s) is just 1. That is, JH=1.
mihirb
2015-02-26 19:21:32
now for DC
now for DC
DPatrick
2015-02-26 19:21:43
And we also remember that DC=r=1+s.
And we also remember that DC=r=1+s.
DPatrick
2015-02-26 19:22:05
(Again, there are so many different ways in this problem that you could get these quantities. I'm just doing what seemed simplest to me.)
(Again, there are so many different ways in this problem that you could get these quantities. I'm just doing what seemed simplest to me.)
wolfpencil
2015-02-26 19:22:13
1+2s+1
1+2s+1
DPatrick
2015-02-26 19:22:16
Therefore,
FG+JH+CD=s+1+(1+s)=2s+2=2(s+1).
Therefore,
FG+JH+CD=s+1+(1+s)=2s+2=2(s+1).
Darn
2015-02-26 19:22:36
So add and get ;1+√5→D
So add and get ;1+√5→D
WalkerTesla
2015-02-26 19:22:36
Which is equal to 1+√5 or D
Which is equal to 1+√5 or D
DPatrick
2015-02-26 19:22:40
Now we compute:
2(s+1)=2(√5−12+1)=(√5−1)+2=√5+1,
answer (D).
Now we compute:
2(s+1)=2(√5−12+1)=(√5−1)+2=√5+1,
answer (D).
DPatrick
2015-02-26 19:23:13
On to 10B #23:
On to 10B #23:
DPatrick
2015-02-26 19:23:20
23. Let n be a positive integer greater than 4 such that the decimal representation of n! ends in k zeros and the decimal representation of (2n)! ends in 3k zeros. Let s denote the sum of the four least possible values of n. What is the sum of the digits of s?
10B:23
(A) 7(B) 8(C) 9(D) 10(E) 11
23. Let n be a positive integer greater than 4 such that the decimal representation of n! ends in k zeros and the decimal representation of (2n)! ends in 3k zeros. Let s denote the sum of the four least possible values of n. What is the sum of the digits of s?
10B:23
(A) 7(B) 8(C) 9(D) 10(E) 11
DPatrick
2015-02-26 19:23:41
How do we determine the number of zeros at the end of n!?
How do we determine the number of zeros at the end of n!?
Deathranger999
2015-02-26 19:23:56
It's a function of how many fives are in each factorial.
It's a function of how many fives are in each factorial.
ktbroborg
2015-02-26 19:23:56
number of 0s is number of pairs of 2s and 5s
number of 0s is number of pairs of 2s and 5s
nosyarg
2015-02-26 19:23:56
look at 5's and 2's
look at 5's and 2's
donot
2015-02-26 19:23:56
Multiples of 5
Multiples of 5
AMN300
2015-02-26 19:23:56
number of 5's
number of 5's
TheMaskedMagician
2015-02-26 19:23:56
Number of factors of 5
Number of factors of 5
willalphagamma
2015-02-26 19:23:56
The factors of 5
The factors of 5
IDontWannaPlay
2015-02-26 19:23:56
see how many factors of 10 there are
see how many factors of 10 there are
WhaleVomit
2015-02-26 19:23:56
how many factors of 5 it has
how many factors of 5 it has
hibiscus
2015-02-26 19:23:56
number of factors of 5
number of factors of 5
akim99
2015-02-26 19:23:56
The number of 5s.
The number of 5s.
Benaloo26
2015-02-26 19:23:56
Factors of 5
Factors of 5
DPatrick
2015-02-26 19:24:02
We need to count the number of factors of 10 in n!.
We need to count the number of factors of 10 in n!.
DPatrick
2015-02-26 19:24:07
But 10's are made of up 2's and 5's, and n! will have lots more 2's than 5's.
But 10's are made of up 2's and 5's, and n! will have lots more 2's than 5's.
DPatrick
2015-02-26 19:24:14
So the number of zeros at the end of n! is just the number of factors of 5 of n!.
So the number of zeros at the end of n! is just the number of factors of 5 of n!.
anandiyer12
2015-02-26 19:24:31
start off with small numbers?
start off with small numbers?
flyrain
2015-02-26 19:24:31
you can just grind it out and find the 4 numbers
you can just grind it out and find the 4 numbers
fractal161
2015-02-26 19:24:31
Organized casework.
Organized casework.
DPatrick
2015-02-26 19:24:40
Sure, one idea is to just experiment a little bit.
Sure, one idea is to just experiment a little bit.
DPatrick
2015-02-26 19:24:47
For example: for what values of n does n! have 1 zero at the end?
For example: for what values of n does n! have 1 zero at the end?
math-rules
2015-02-26 19:25:27
5-9
5-9
nosaj
2015-02-26 19:25:27
5-9
5-9
BFYSharks
2015-02-26 19:25:27
5-9
5-9
fluffyanimal
2015-02-26 19:25:27
5,6,7,8,9
5,6,7,8,9
_--__--_
2015-02-26 19:25:27
5,6,7,8,9
5,6,7,8,9
DrMath
2015-02-26 19:25:27
5,6,7,8,9
5,6,7,8,9
tdeng
2015-02-26 19:25:27
5-9
5-9
ingridzhang97
2015-02-26 19:25:27
5-9
5-9
acegikmoqsuwy2000
2015-02-26 19:25:27
5,6,7,8,9
5,6,7,8,9
bluephoenix
2015-02-26 19:25:27
5,6,7,8,9
5,6,7,8,9
geogirl08
2015-02-26 19:25:27
5, 6, 7, 8, 9
5, 6, 7, 8, 9
DPatrick
2015-02-26 19:25:48
Right: n=5,6,7,8,9 have only 1 factor of 5.
Right: n=5,6,7,8,9 have only 1 factor of 5.
DPatrick
2015-02-26 19:25:55
For any of these, does (2n)! have 3 zeros at the end?
For any of these, does (2n)! have 3 zeros at the end?
FrozenFire31415
2015-02-26 19:26:22
8 and 9
8 and 9
baseballlogic
2015-02-26 19:26:22
8, 9
8, 9
abishek99
2015-02-26 19:26:22
8 and 9
8 and 9
rjiang16
2015-02-26 19:26:22
8,9
8,9
antler
2015-02-26 19:26:22
only 8 and 9
only 8 and 9
ninjataco
2015-02-26 19:26:22
8 and 9
8 and 9
DPatrick
2015-02-26 19:26:33
Note (2n)! will have 3 zeros if and only if 2n=15,16,17,18,19.
Note (2n)! will have 3 zeros if and only if 2n=15,16,17,18,19.
DPatrick
2015-02-26 19:26:40
So n=8,2n=16 works, and n=9,2n=18 works.
So n=8,2n=16 works, and n=9,2n=18 works.
DPatrick
2015-02-26 19:26:49
That's two values! We only need two more!
That's two values! We only need two more!
DPatrick
2015-02-26 19:26:58
Moving on...for what values of n does n! have 2 zeros at the end?
Moving on...for what values of n does n! have 2 zeros at the end?
aadavi
2015-02-26 19:27:21
10-14
10-14
yamyamx2
2015-02-26 19:27:21
10-14
10-14
bengals
2015-02-26 19:27:21
10-14
10-14
gradysocool
2015-02-26 19:27:21
10-14
10-14
Turtwig123
2015-02-26 19:27:21
10-14
10-14
123456789agarwal
2015-02-26 19:27:21
10-14
10-14
tau172
2015-02-26 19:27:21
10 to 14
10 to 14
speck
2015-02-26 19:27:21
10,11,12,13,14
10,11,12,13,14
LOTRFan123
2015-02-26 19:27:21
10 -14
10 -14
az_phx_brandon_jiang
2015-02-26 19:27:21
10-14
10-14
DPatrick
2015-02-26 19:27:25
n=10,11,12,13,14
n=10,11,12,13,14
DPatrick
2015-02-26 19:27:29
For which (if any) of these does (2n)! have 6 zeros?
For which (if any) of these does (2n)! have 6 zeros?
Shark77
2015-02-26 19:28:00
13, 14
13, 14
kunsun
2015-02-26 19:28:00
13 and 14, because 10-14 has 2 zeroes and 25-29 has 6 zeroes
13 and 14, because 10-14 has 2 zeroes and 25-29 has 6 zeroes
Not_a_Username
2015-02-26 19:28:00
13, 14
13, 14
problemsolver12
2015-02-26 19:28:00
13, 14
13, 14
Tuxianeer
2015-02-26 19:28:00
13,14,
13,14,
Mathlete55
2015-02-26 19:28:00
13, 14
13, 14
lucylai
2015-02-26 19:28:00
13,14
13,14
AlcumusGuy
2015-02-26 19:28:00
13 and 14
13 and 14
abean077
2015-02-26 19:28:00
13 and 14
13 and 14
DPatrick
2015-02-26 19:28:04
Note that 2n=25,26,27,28,29 each satisfies (2n)! with 6 zeros, because the factor of 25 gives an "extra" factor of 5.
Note that 2n=25,26,27,28,29 each satisfies (2n)! with 6 zeros, because the factor of 25 gives an "extra" factor of 5.
DPatrick
2015-02-26 19:28:13
So n=13,2n=26 works, as does n=14,2n=28.
So n=13,2n=26 works, as does n=14,2n=28.
DPatrick
2015-02-26 19:28:21
But now we're done! We've found the 4 smallest values of n: 8, 9, 13, and 14.
But now we're done! We've found the 4 smallest values of n: 8, 9, 13, and 14.
Darn
2015-02-26 19:28:52
Thus our answer is 8+9+13+14=44→(B) 8
Thus our answer is 8+9+13+14=44→(B) 8
wolfpencil
2015-02-26 19:28:52
add them up, then find the sum of the digits
add them up, then find the sum of the digits
Modest_Ked
2015-02-26 19:28:52
The answer is 8
The answer is 8
akim99
2015-02-26 19:28:52
8+9+13+14 = 44 ==> 8, so (B).
8+9+13+14 = 44 ==> 8, so (B).
pad
2015-02-26 19:28:52
s=8+9+13+14=44
s=8+9+13+14=44
DPatrick
2015-02-26 19:28:57
Their sum is s=8+9+13+14=44, and the sum of the digits of s is 4+4=8. Answer (B).
Their sum is s=8+9+13+14=44, and the sum of the digits of s is 4+4=8. Answer (B).
Turtwig123
2015-02-26 19:29:05
are these the only values?
are these the only values?
DPatrick
2015-02-26 19:29:26
That's an interesting question. (Of course, on the AMC contest itself, you wouldn't waste time thinking about it.)
That's an interesting question. (Of course, on the AMC contest itself, you wouldn't waste time thinking about it.)
DPatrick
2015-02-26 19:29:46
It turns out these are the only 4 values that work!
It turns out these are the only 4 values that work!
DPatrick
2015-02-26 19:29:52
Let's quickly digress and see why.
Let's quickly digress and see why.
DPatrick
2015-02-26 19:30:07
Given a value n, what's a formula for the number of factors of 5 in n! (and thus the number of zeros at the end of n!)?
Given a value n, what's a formula for the number of factors of 5 in n! (and thus the number of zeros at the end of n!)?
AMN300
2015-02-26 19:30:29
floor(n/5)+floor(n/25)+...
floor(n/5)+floor(n/25)+...
speck
2015-02-26 19:30:29
floor(n/5)+floor(n/25)+...
floor(n/5)+floor(n/25)+...
akim99
2015-02-26 19:30:29
Floor function of n/5 + floor of n/25 + ...
Floor function of n/5 + floor of n/25 + ...
_--__--_
2015-02-26 19:30:29
floor(n/5) + floor(n/25) + floor(n/125) + ....
floor(n/5) + floor(n/25) + floor(n/125) + ....
DPatrick
2015-02-26 19:30:36
Right. If n! ends in k zeros, then
k=⌊n5⌋+⌊n52⌋+⌊n53⌋+⋯.
Right. If n! ends in k zeros, then
k=⌊n5⌋+⌊n52⌋+⌊n53⌋+⋯.
DPatrick
2015-02-26 19:30:54
That symbol is the floor function, which (for positive numbers) means round DOWN to the nearest integer.
That symbol is the floor function, which (for positive numbers) means round DOWN to the nearest integer.
DPatrick
2015-02-26 19:31:02
The first term counts the number of terms in n! that are multiples of 5.
The second term counts the number of terms in n! that are multiples of 52 (and thus contribute an extra factor of 5).
The third term counts the number of terms in n! that are multiples of 53 (and thus contribute an extra factor of 5 beyond the two already counted).
And so on.
The first term counts the number of terms in n! that are multiples of 5.
The second term counts the number of terms in n! that are multiples of 52 (and thus contribute an extra factor of 5).
The third term counts the number of terms in n! that are multiples of 53 (and thus contribute an extra factor of 5 beyond the two already counted).
And so on.
DPatrick
2015-02-26 19:31:20
So if (2n)! has 3k zeros, we must have
3k=⌊2n5⌋+⌊2n52⌋+⌊2n53⌋+⋯.
So if (2n)! has 3k zeros, we must have
3k=⌊2n5⌋+⌊2n52⌋+⌊2n53⌋+⋯.
DPatrick
2015-02-26 19:31:31
But how is ⌊n5j⌋ related to ⌊2n5j⌋ for some j?
But how is ⌊n5j⌋ related to ⌊2n5j⌋ for some j?
DPatrick
2015-02-26 19:31:37
More generally, how are ⌊x⌋ and ⌊2x⌋ related for any positive x?
More generally, how are ⌊x⌋ and ⌊2x⌋ related for any positive x?
WalkerTesla
2015-02-26 19:32:00
The second is double the first or 1 more than double the first
The second is double the first or 1 more than double the first
hibiscus
2015-02-26 19:32:00
It depends on the fractional part of x.
It depends on the fractional part of x.
flyrain
2015-02-26 19:32:04
they're at most 1 apart
they're at most 1 apart
DPatrick
2015-02-26 19:32:10
Right. If the fractional part of x is less than 0.5, then ⌊2x⌋=2⌊x⌋. (For example, ⌊3.2⌋=3 and doubling it gives ⌊6.4⌋=6.)
Right. If the fractional part of x is less than 0.5, then ⌊2x⌋=2⌊x⌋. (For example, ⌊3.2⌋=3 and doubling it gives ⌊6.4⌋=6.)
DPatrick
2015-02-26 19:32:17
If the fractional part of x is at least 0.5, then ⌊2x⌋=2⌊x⌋+1. (For example, ⌊3.8⌋=3 and doubling it gives ⌊7.6⌋=7.)
If the fractional part of x is at least 0.5, then ⌊2x⌋=2⌊x⌋+1. (For example, ⌊3.8⌋=3 and doubling it gives ⌊7.6⌋=7.)
nosaj
2015-02-26 19:32:28
either floor(2x)=2floor(x) of floor(2x)=2floor(x)+1
either floor(2x)=2floor(x) of floor(2x)=2floor(x)+1
DPatrick
2015-02-26 19:32:37
Right, or to say it another way, ⌊2x⌋=2⌊x⌋+ϵ, where ϵ can be 0 or 1.
Right, or to say it another way, ⌊2x⌋=2⌊x⌋+ϵ, where ϵ can be 0 or 1.
DPatrick
2015-02-26 19:32:48
So when we go from n! to (2n)!, each floor term will double the number of zeros, and possibly add 1 more zero. Plus we might get one extra zero at the end if 2n jumps across the next power of 5 (like our example n=13,2n=26 from before.)
So when we go from n! to (2n)!, each floor term will double the number of zeros, and possibly add 1 more zero. Plus we might get one extra zero at the end if 2n jumps across the next power of 5 (like our example n=13,2n=26 from before.)
DrMath
2015-02-26 19:33:14
well we need to add that 1 exactly k times
well we need to add that 1 exactly k times
DPatrick
2015-02-26 19:33:20
Right. In addition to the 2k zeros that we're guaranteed to have, we might have an additional m+1 zeros, where m satisfies 5m≤n<5m+1.
Right. In addition to the 2k zeros that we're guaranteed to have, we might have an additional m+1 zeros, where m satisfies 5m≤n<5m+1.
DPatrick
2015-02-26 19:33:28
(If you know logarithms, then you know that m=⌊log5n⌋.)
(If you know logarithms, then you know that m=⌊log5n⌋.)
DPatrick
2015-02-26 19:33:40
But to get 3k zeros total, we need to have k of these ``extra'' zeroes, so we need k≤m+1.
But to get 3k zeros total, we need to have k of these ``extra'' zeroes, so we need k≤m+1.
DPatrick
2015-02-26 19:34:17
On the other hand, we know that if 5m≤n, so we have
k≥⌊5m5⌋+⌊5m52⌋+⌊5m53⌋+⋯+⌊5m5m⌋=5(m−1)+(m−2)+⋯+1=5(m(m−1)2).
On the other hand, we know that if 5m≤n, so we have
k≥⌊5m5⌋+⌊5m52⌋+⌊5m53⌋+⋯+⌊5m5m⌋=5(m−1)+(m−2)+⋯+1=5(m(m−1)2).
DPatrick
2015-02-26 19:34:56
That's a big number. It's really hard for that number to be less than m+1.
That's a big number. It's really hard for that number to be less than m+1.
DPatrick
2015-02-26 19:35:08
Specifically, we must have
5(m(m−1)2)≤k≤m+1.
Specifically, we must have
5(m(m−1)2)≤k≤m+1.
DPatrick
2015-02-26 19:35:34
Since n>4, we have m>0, and this only holds for m=1. (The powers-of-5 term is already bigger than m+1 when m=2, and it grows much much faster than m+1 as m grows!)
Since n>4, we have m>0, and this only holds for m=1. (The powers-of-5 term is already bigger than m+1 when m=2, and it grows much much faster than m+1 as m grows!)
DPatrick
2015-02-26 19:35:55
The upshot is: all this algebra proves that we only need to look at n satisfying 5≤n<25, and then trial-and-error finds just the 4 solutions that we found using our original experimental method. It turns out that not only are 8,9,13,14 the four smallest values of n that work, they're the only values of n that work!
The upshot is: all this algebra proves that we only need to look at n satisfying 5≤n<25, and then trial-and-error finds just the 4 solutions that we found using our original experimental method. It turns out that not only are 8,9,13,14 the four smallest values of n that work, they're the only values of n that work!
swirlykick
2015-02-26 19:36:06
Would if have been better to say find the sum of all n? finding the 4 values of n didnt seem very hard
Would if have been better to say find the sum of all n? finding the 4 values of n didnt seem very hard
DPatrick
2015-02-26 19:36:28
I think "finding them all" might have been too hard for an AMC 10. I mentioned logarithms above, for example, which is beyond the scope of the AMC 10.
I think "finding them all" might have been too hard for an AMC 10. I mentioned logarithms above, for example, which is beyond the scope of the AMC 10.
DPatrick
2015-02-26 19:36:49
Anyway...on to 10B #24:
Anyway...on to 10B #24:
DPatrick
2015-02-26 19:36:56
24. Aaron the ant walks on the coordinate plane according to the following rules. He starts at the origin p0=(0,0) facing to the east and walks one unit, arriving at p1=(1,0). For n=1,2,3,…, right after arriving at the point pn, if Aaron can turn 90∘ left and walk one unit to an unvisited point pn+1, he does that. Otherwise, he walks one unit straight ahead to reach pn+1. Thus the sequence of points continues p2=(1,1), p3=(0,1), p4=(−1,1), p5=(−1,0), and so on in a counterclockwise spiral pattern. What is p2015?
10B:24
(A) (−22,−13)(B) (−13,−22)(C) (−13,22)(D) (13,−22)(E) (22,−13)
24. Aaron the ant walks on the coordinate plane according to the following rules. He starts at the origin p0=(0,0) facing to the east and walks one unit, arriving at p1=(1,0). For n=1,2,3,…, right after arriving at the point pn, if Aaron can turn 90∘ left and walk one unit to an unvisited point pn+1, he does that. Otherwise, he walks one unit straight ahead to reach pn+1. Thus the sequence of points continues p2=(1,1), p3=(0,1), p4=(−1,1), p5=(−1,0), and so on in a counterclockwise spiral pattern. What is p2015?
10B:24
(A) (−22,−13)(B) (−13,−22)(C) (−13,22)(D) (13,−22)(E) (22,−13)
PresidentJL
2015-02-26 19:37:18
Draw a diagram
Draw a diagram
mihirb
2015-02-26 19:37:18
try to find a pattern
try to find a pattern
AlcumusGuy
2015-02-26 19:37:18
Find a pattern
Find a pattern
Not_a_Username
2015-02-26 19:37:18
Draw it out and find a pattern
Draw it out and find a pattern
ompatel99
2015-02-26 19:37:18
Picture!
Picture!
bengals
2015-02-26 19:37:18
Draw a picture
Draw a picture
Darn
2015-02-26 19:37:18
Write out the first few
Write out the first few
15Pandabears
2015-02-26 19:37:18
pattern
pattern
mjoshi
2015-02-26 19:37:18
draw out a first few
draw out a first few
DPatrick
2015-02-26 19:37:22
This is mainly a bookkeeping problem. We just need to keep careful track of where Aaron is after n moves.
This is mainly a bookkeeping problem. We just need to keep careful track of where Aaron is after n moves.
DPatrick
2015-02-26 19:37:30
Here's a picture of his path:
Here's a picture of his path:
DPatrick
2015-02-26 19:37:35
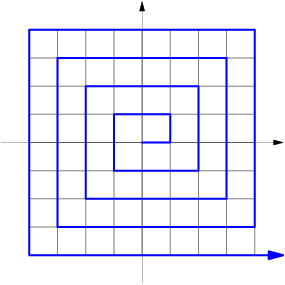

DPatrick
2015-02-26 19:38:11
Probably a good idea is to try to quantify when he gets to the corners somehow.
Probably a good idea is to try to quantify when he gets to the corners somehow.
_--__--_
2015-02-26 19:38:18
Distance traveled is 1+1+2+2+3+3+4+4+...
Distance traveled is 1+1+2+2+3+3+4+4+...
abean077
2015-02-26 19:38:24
Notice the first two line segments are 1, then the next two are 2, and so on
Notice the first two line segments are 1, then the next two are 2, and so on
DPatrick
2015-02-26 19:38:34
Yes, I found that to be a really helpful observation!
Yes, I found that to be a really helpful observation!
DPatrick
2015-02-26 19:38:38
He starts by taking 1 step E and 1 step N, ending at (1,1) after 2 steps and about to head W.
He starts by taking 1 step E and 1 step N, ending at (1,1) after 2 steps and about to head W.
DPatrick
2015-02-26 19:38:44
Then he takes 2 steps W and 2 steps S, ending at (-1,-1) after 2+4 steps, and about to head E.
Then he takes 2 steps W and 2 steps S, ending at (-1,-1) after 2+4 steps, and about to head E.
DPatrick
2015-02-26 19:38:51
Then he takes 3 steps E and 3 steps N, ending at (2,2) after 2+4+6 steps, and about to head W.
Then he takes 3 steps E and 3 steps N, ending at (2,2) after 2+4+6 steps, and about to head W.
DPatrick
2015-02-26 19:39:01
Then he takes 4 steps W and 4 steps S, ending at (-2,-2) after 2+4+6+8 steps, and about to head E.
Then he takes 4 steps W and 4 steps S, ending at (-2,-2) after 2+4+6+8 steps, and about to head E.
DPatrick
2015-02-26 19:39:06
Is there a convenient formula for the number of steps to some general point?
Is there a convenient formula for the number of steps to some general point?
Deathranger999
2015-02-26 19:39:13
So triangular numbers, times 2!
So triangular numbers, times 2!
RBMS14
2015-02-26 19:39:33
triangle numbers
triangle numbers
DPatrick
2015-02-26 19:40:01
So there are a lot of choices we could make here for which point to compute.
So there are a lot of choices we could make here for which point to compute.
DPatrick
2015-02-26 19:40:17
But the ones listed above all involve 2 times the triangular numbers 1+2+...+n
But the ones listed above all involve 2 times the triangular numbers 1+2+...+n
BFYSharks
2015-02-26 19:40:24
Bottom left corner! (-n, -n)
Bottom left corner! (-n, -n)
DPatrick
2015-02-26 19:40:42
That's what I did. We can notice that for any integer k≥1, he's at (−k,−k) after 2+4+6+⋯+4k steps, and about to head E. This sum is easy to compute in terms of k.
That's what I did. We can notice that for any integer k≥1, he's at (−k,−k) after 2+4+6+⋯+4k steps, and about to head E. This sum is easy to compute in terms of k.
DPatrick
2015-02-26 19:41:19
There are 2k terms in the sum, with an average value of (2+4k)/2=2k+1, so
2+4+6+⋯+4k=2k(2k+1).
There are 2k terms in the sum, with an average value of (2+4k)/2=2k+1, so
2+4+6+⋯+4k=2k(2k+1).
blueduck1
2015-02-26 19:41:40
So P(1980) is -22,-22
So P(1980) is -22,-22
mattpi
2015-02-26 19:41:40
the 1980th position is at -22, -22, so the 2015th position is 13, -22 (D)
the 1980th position is at -22, -22, so the 2015th position is 13, -22 (D)
DPatrick
2015-02-26 19:41:54
Exactly. k=22 gives 44(45)=1980<2015.
Exactly. k=22 gives 44(45)=1980<2015.
DPatrick
2015-02-26 19:42:00
Thus, after 1980 moves, Aaron is at (-22,-22) and is heading east.
Thus, after 1980 moves, Aaron is at (-22,-22) and is heading east.
DPatrick
2015-02-26 19:42:12
(The answer choices are also a big clue to look at k=22!)
(The answer choices are also a big clue to look at k=22!)
AMN300
2015-02-26 19:42:35
so (13, -22) D
so (13, -22) D
DPatrick
2015-02-26 19:42:37
He's got 2015 - 1980 = 35 moves to go. He won't turn again until he hits (23,-22). So he moves 35 spaces east, ending up at (-22+35,-22) = (13,-22). Answer (D).
He's got 2015 - 1980 = 35 moves to go. He won't turn again until he hits (23,-22). So he moves 35 spaces east, ending up at (-22+35,-22) = (13,-22). Answer (D).
DPatrick
2015-02-26 19:43:17
There are lots of other pattens you could have used in this problem probably just as easily.
There are lots of other pattens you could have used in this problem probably just as easily.
DPatrick
2015-02-26 19:43:42
But in general I don't find these "bookkeeping" sort of problems all that interesting, so let's move on...
But in general I don't find these "bookkeeping" sort of problems all that interesting, so let's move on...
DPatrick
2015-02-26 19:43:50
Next is 10B #25, which was also 12B #23:
Next is 10B #25, which was also 12B #23:
DPatrick
2015-02-26 19:43:54
25. A rectangular box measures a×b×c, where a, b, and c are integers and 1≤a≤b≤c. The volume and the surface area of the box are numerically equal. How many ordered triples (a,b,c) are possible?
10B:25
(A) 4(B) 10(C) 12(D) 21(E) 26
25. A rectangular box measures a×b×c, where a, b, and c are integers and 1≤a≤b≤c. The volume and the surface area of the box are numerically equal. How many ordered triples (a,b,c) are possible?
10B:25
(A) 4(B) 10(C) 12(D) 21(E) 26
acegikmoqsuwy2000
2015-02-26 19:44:23
abc=2(ab+bc+ac)
abc=2(ab+bc+ac)
Darn
2015-02-26 19:44:23
Write this as abc=2(ab+bc+ac)
Write this as abc=2(ab+bc+ac)
Not_a_Username
2015-02-26 19:44:23
Set up an equation: abc=2ab+2ac+2bc
Set up an equation: abc=2ab+2ac+2bc
Deathranger999
2015-02-26 19:44:23
abc = 2(ab + bc + ca)
abc = 2(ab + bc + ca)
ompatel99
2015-02-26 19:44:23
Volume=abc=SA=2(ab+bc+ac)
Volume=abc=SA=2(ab+bc+ac)
AlcumusGuy
2015-02-26 19:44:23
Write an equation: abc = 2(ab + bc + ca)
Write an equation: abc = 2(ab + bc + ca)
_--__--_
2015-02-26 19:44:23
abc = 2(ab + ac + bc)
abc = 2(ab + ac + bc)
DrMath
2015-02-26 19:44:23
abc=2(ab+bc+ca)
abc=2(ab+bc+ca)
bluephoenix
2015-02-26 19:44:23
abc = 2ab+2bc+2ac
abc = 2ab+2bc+2ac
mathtastic
2015-02-26 19:44:23
abc=2ab+2bc+2ca
abc=2ab+2bc+2ca
droid347
2015-02-26 19:44:23
We know abc=2(ab+bc+ca) by formulas for volume and surface area.
We know abc=2(ab+bc+ca) by formulas for volume and surface area.
DPatrick
2015-02-26 19:44:27
The volume of the box is abc.
The volume of the box is abc.
DPatrick
2015-02-26 19:44:31
The box has two sides with area ab, two sides with area ac, and two sides with area bc.
The box has two sides with area ab, two sides with area ac, and two sides with area bc.
DPatrick
2015-02-26 19:44:38
Thus we're trying to solve
abc=2(ab+ac+bc).
Thus we're trying to solve
abc=2(ab+ac+bc).
DPatrick
2015-02-26 19:44:45
How can we work with this equation?
How can we work with this equation?
AMN300
2015-02-26 19:44:57
Divide both sides by 2abc to simplify a little
Divide both sides by 2abc to simplify a little
Not_a_Username
2015-02-26 19:44:57
Divide both sides by 2abc
Divide both sides by 2abc
nosaj
2015-02-26 19:44:57
We must have abc=2ab+2ac+2bc. Dividing both sides of the equation by 2abc yields the (simple) equation 1a+1b+1c=12.
We must have abc=2ab+2ac+2bc. Dividing both sides of the equation by 2abc yields the (simple) equation 1a+1b+1c=12.
bestwillcui1
2015-02-26 19:44:57
divide through by 2abc
divide through by 2abc
TheMaskedMagician
2015-02-26 19:44:57
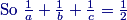
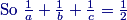
numbersandnumbers
2015-02-26 19:44:57
divide by 2abc
divide by 2abc
DPatrick
2015-02-26 19:45:03
One idea is to make the terms simpler, by dividing through by 2abc. This gives
12=1a+1b+1c.
One idea is to make the terms simpler, by dividing through by 2abc. This gives
12=1a+1b+1c.
DPatrick
2015-02-26 19:45:07
What does this tell us?
What does this tell us?
ingridzhang97
2015-02-26 19:45:32
a,b,c>2
a,b,c>2
rjiang16
2015-02-26 19:45:32
we know a, b, c all greater than 2
we know a, b, c all greater than 2
vinayak-kumar
2015-02-26 19:45:32
A>2
A>2
DPatrick
2015-02-26 19:45:36
This tells us right away that a,b,c≥3. Otherwise, if any of the denominators are 1 or 2, then the right side is too big.
This tells us right away that a,b,c≥3. Otherwise, if any of the denominators are 1 or 2, then the right side is too big.
jigglypuff
2015-02-26 19:45:58
a is between 3 and 6
a is between 3 and 6
Darn
2015-02-26 19:45:58
2≤a≤6
2≤a≤6
AlcumusGuy
2015-02-26 19:45:58
a <= 6, as otherwise we cannot sum to 1/2
a <= 6, as otherwise we cannot sum to 1/2
amburger66
2015-02-26 19:45:58
a,b,c are less than or equal to 6
a,b,c are less than or equal to 6
DrMath
2015-02-26 19:45:58
well the greatest value among 1/a,1/b,1/c is ≥1/6
well the greatest value among 1/a,1/b,1/c is ≥1/6
AllenWang314
2015-02-26 19:46:03
a,b,c≤6
a,b,c≤6
DPatrick
2015-02-26 19:46:10
Also remember that a≤b≤c, so that 1a≥1b≥1c.
Also remember that a≤b≤c, so that 1a≥1b≥1c.
DPatrick
2015-02-26 19:46:13
So this also tells us that a≤6. Otherwise (if a>6) all the right-side terms are less than 16, so the right side is too small.
So this also tells us that a≤6. Otherwise (if a>6) all the right-side terms are less than 16, so the right side is too small.
DPatrick
2015-02-26 19:46:33
And what happens if a=6?
And what happens if a=6?
bluehall90
2015-02-26 19:47:00
b=6 and c=6
b=6 and c=6
acegikmoqsuwy2000
2015-02-26 19:47:00
b=c=6
b=c=6
bfea
2015-02-26 19:47:00
b and c are 6
b and c are 6
stealbob
2015-02-26 19:47:00
b adn c are 6 as well
b adn c are 6 as well
ninjataco
2015-02-26 19:47:00
a=b=c=6
a=b=c=6
MathLearner01
2015-02-26 19:47:00
a=b=c=6
a=b=c=6
Benaloo26
2015-02-26 19:47:00
b and c = 6
b and c = 6
abean077
2015-02-26 19:47:00
b = 6 and c = 6
b = 6 and c = 6
Imagineny1
2015-02-26 19:47:00
b=c=6
b=c=6
DPatrick
2015-02-26 19:47:06
It also tells us that the only solution with a=6 is a=b=c=6: all three terms on the right side are 16. That's 1 solution.
It also tells us that the only solution with a=6 is a=b=c=6: all three terms on the right side are 16. That's 1 solution.
DPatrick
2015-02-26 19:47:22
So we have three cases left: a=3, a=4, or a=5. I don't know of a slick way to solve this except to do the cases one by one.
So we have three cases left: a=3, a=4, or a=5. I don't know of a slick way to solve this except to do the cases one by one.
Darn
2015-02-26 19:47:44
Casework!
Casework!
DPatrick
2015-02-26 19:47:52
If a=3, we get
16=1b+1c
with the restriction that 3≤b≤c.
If a=3, we get
16=1b+1c
with the restriction that 3≤b≤c.
bluehall90
2015-02-26 19:48:25
And b =< 12
And b =< 12
fluffyanimal
2015-02-26 19:48:25
6<b<=12
6<b<=12
abean077
2015-02-26 19:48:25
b = c = 12 is one way
b = c = 12 is one way
DPatrick
2015-02-26 19:48:28
We could use the same idea: use bounding to show that we must have 6≤b≤12, and see which of these work.
We could use the same idea: use bounding to show that we must have 6≤b≤12, and see which of these work.
DPatrick
2015-02-26 19:48:36
But there's a more clever way. Let's go back to the original form of the equation and substitute in a=3:
3bc=2(3b+3c+bc).
But there's a more clever way. Let's go back to the original form of the equation and substitute in a=3:
3bc=2(3b+3c+bc).
pnpiano
2015-02-26 19:49:04
we can rearrange and then use simon's favorite factoring trick
we can rearrange and then use simon's favorite factoring trick
pnpiano
2015-02-26 19:49:04
SFFT right?
SFFT right?
BFYSharks
2015-02-26 19:49:04
SFFT
SFFT
NumberNinja
2015-02-26 19:49:04
SFFT
SFFT
az_phx_brandon_jiang
2015-02-26 19:49:04
expand and factor
expand and factor
DPatrick
2015-02-26 19:49:09
This simplifies to bc−6b−6c=0.
This simplifies to bc−6b−6c=0.
DPatrick
2015-02-26 19:49:15
And now we use Simon's Favorite Factoring Trick!
And now we use Simon's Favorite Factoring Trick!
DPatrick
2015-02-26 19:49:24
If you haven't seen SFFT before, the idea is to add a constant to both sides so that one side can factor. What constant should we add?
If you haven't seen SFFT before, the idea is to add a constant to both sides so that one side can factor. What constant should we add?
SHARKYBOY
2015-02-26 19:49:45
36
36
geogirl08
2015-02-26 19:49:45
36
36
15Pandabears
2015-02-26 19:49:45
36
36
eswa2000
2015-02-26 19:49:45
36
36
dli00105
2015-02-26 19:49:45
36
36
mathboxboro
2015-02-26 19:49:45
36
36
DPatrick
2015-02-26 19:49:50
I'd add 36, to give bc−6b−6c+36=36. Now it factors as
(b−6)(c−6)=36.
What are the integer solutions to this?
I'd add 36, to give bc−6b−6c+36=36. Now it factors as
(b−6)(c−6)=36.
What are the integer solutions to this?
donot
2015-02-26 19:50:36
we factor bash
we factor bash
jam10307
2015-02-26 19:50:36
factors of 36
factors of 36
jigglypuff
2015-02-26 19:50:36
1*36,2*18,3*12,4*9,6*6 and add 6 to all of them
1*36,2*18,3*12,4*9,6*6 and add 6 to all of them
DPatrick
2015-02-26 19:50:41
Right. 36 can be factored 5 ways: 6⋅6, 4⋅9, 3⋅12, 2⋅18, 1⋅36.
Right. 36 can be factored 5 ways: 6⋅6, 4⋅9, 3⋅12, 2⋅18, 1⋅36.
DPatrick
2015-02-26 19:50:58
Since b≤c, all of these must assign b−6 to the smaller factor, and c−6 to the larger factor.
Since b≤c, all of these must assign b−6 to the smaller factor, and c−6 to the larger factor.
DPatrick
2015-02-26 19:51:06
Adding 6 to each of these gives a solution to (b,c) for a=3: (12,12), (10,15), (9,18), (8,24), (7,42).
Adding 6 to each of these gives a solution to (b,c) for a=3: (12,12), (10,15), (9,18), (8,24), (7,42).
DPatrick
2015-02-26 19:51:13
Note that all of these have 3≤b≤c, so they're all valid solutions.
Note that all of these have 3≤b≤c, so they're all valid solutions.
mathcountsprep
2015-02-26 19:51:24
so 5 ways
so 5 ways
Not_a_Username
2015-02-26 19:51:24
5 triples.
5 triples.
SimonSun
2015-02-26 19:51:24
5 soltions
5 soltions
DPatrick
2015-02-26 19:51:27
So that's 5 more solutions. We're up to 6 solutions total.
So that's 5 more solutions. We're up to 6 solutions total.
ryansong2002
2015-02-26 19:51:39
now on the a=4
now on the a=4
rjiang16
2015-02-26 19:51:39
a=4 case
a=4 case
ninjataco
2015-02-26 19:51:39
now onto a=4!
now onto a=4!
DPatrick
2015-02-26 19:51:41
Now on to a=4.
Now on to a=4.
DPatrick
2015-02-26 19:51:47
We again plug this into the original
4bc=2(4b+4c+bc).
We again plug this into the original
4bc=2(4b+4c+bc).
DPatrick
2015-02-26 19:51:56
This simplifies to 2bc−8b−8c=0.
Divide by 2 to get bc−4b−4c=0.
This simplifies to 2bc−8b−8c=0.
Divide by 2 to get bc−4b−4c=0.
problemsolver12
2015-02-26 19:52:11
SFFT again
SFFT again
pad
2015-02-26 19:52:11
sfft!
sfft!
Zynaria
2015-02-26 19:52:11
16
16
bluephoenix
2015-02-26 19:52:11
add 16
add 16
fractal161
2015-02-26 19:52:11
SFFT with 16
SFFT with 16
AMN300
2015-02-26 19:52:11
add 16 to both sides
add 16 to both sides
mathymath
2015-02-26 19:52:11
sfft again
sfft again
pisgood
2015-02-26 19:52:11
Add by 16
Add by 16
hibiscus
2015-02-26 19:52:11
(b-4)(c-4)=16
(b-4)(c-4)=16
ingridzhang97
2015-02-26 19:52:11
(b-4)(c-4)=16
(b-4)(c-4)=16
DPatrick
2015-02-26 19:52:29
Good -- we SFFT again! Add 16 to both sides:
bc−4b−4c+16=16.
This factors to (b−4)(c−4)=16.
Good -- we SFFT again! Add 16 to both sides:
bc−4b−4c+16=16.
This factors to (b−4)(c−4)=16.
DPatrick
2015-02-26 19:52:39
What are the positive integer solutions to this?
What are the positive integer solutions to this?
_--__--_
2015-02-26 19:52:57
(5,20),(6,12),(8,8)
(5,20),(6,12),(8,8)
bestwillcui1
2015-02-26 19:52:57
so just 3
so just 3
flyrain
2015-02-26 19:52:57
and some 3 or so ways from this
and some 3 or so ways from this
rjiang16
2015-02-26 19:52:57
(4,5,20)(4,6,12)(4,8,8)
(4,5,20)(4,6,12)(4,8,8)
Darn
2015-02-26 19:52:57
Notice that we can factor 16 in 3 distinct ways
Notice that we can factor 16 in 3 distinct ways
hibiscus
2015-02-26 19:52:57
(1, 16) (2, 8) (4, 4)
(1, 16) (2, 8) (4, 4)
Jyzhang12
2015-02-26 19:52:57
factor 16 and add 4
factor 16 and add 4
jigglypuff
2015-02-26 19:52:57
1*16,2*8,4*4 and add 4 to all of them
1*16,2*8,4*4 and add 4 to all of them
DPatrick
2015-02-26 19:53:03
16 can be factored 3 ways: 4⋅4, 2⋅8, 1⋅16.
16 can be factored 3 ways: 4⋅4, 2⋅8, 1⋅16.
DPatrick
2015-02-26 19:53:08
Adding 4 to each of these gives a solution to (b,c) for a=4: (8,8), (6,12), (5,20).
Adding 4 to each of these gives a solution to (b,c) for a=4: (8,8), (6,12), (5,20).
mathperson9
2015-02-26 19:53:27
All are valid answers
All are valid answers
rjiang16
2015-02-26 19:53:30
so we have 9 ways total now
so we have 9 ways total now
DPatrick
2015-02-26 19:53:32
All of these have 4≤b≤c, so they're all legal. That's 3 more solutions. We're up to 9 solutions total.
All of these have 4≤b≤c, so they're all legal. That's 3 more solutions. We're up to 9 solutions total.
song2sons
2015-02-26 19:53:42
now a=5
now a=5
mihirb
2015-02-26 19:53:42
now for a = 5
now for a = 5
DPatrick
2015-02-26 19:53:47
Finally we have a=5:
5bc=2(5b+5c+bc).
Finally we have a=5:
5bc=2(5b+5c+bc).
DPatrick
2015-02-26 19:53:52
This simplifies to 3bc−10b−10c=0.
This simplifies to 3bc−10b−10c=0.
crosby87
2015-02-26 19:54:02
SFFT
SFFT
problemsolver12
2015-02-26 19:54:08
SFFT once more
SFFT once more
rjiang16
2015-02-26 19:54:08
harder to SFFT...
harder to SFFT...
DPatrick
2015-02-26 19:54:14
We'd like to use SFFT again, but there doesn't seem to be a nice integer we can add to make it factor.
We'd like to use SFFT again, but there doesn't seem to be a nice integer we can add to make it factor.
nosaj
2015-02-26 19:54:28
Multiply by 3
Multiply by 3
jigglypuff
2015-02-26 19:54:28
multiply by 3 then sfft
multiply by 3 then sfft
nosaj
2015-02-26 19:54:28
9bc-30b-30c=0
9bc-30b-30c=0
jigglypuff
2015-02-26 19:54:28
multiply by 3 then simons
multiply by 3 then simons
DPatrick
2015-02-26 19:54:35
Right. The problem is that 3bc term. Since everything is symmetric in b and c, we'd like to make that 3bc term factor symmetrically too. But the only way to factor it using integer coefficients is 3b⋅c or b⋅3c, and that's not symmetric.
Right. The problem is that 3bc term. Since everything is symmetric in b and c, we'd like to make that 3bc term factor symmetrically too. But the only way to factor it using integer coefficients is 3b⋅c or b⋅3c, and that's not symmetric.
DPatrick
2015-02-26 19:54:44
But we can multiply through by 3:
9bc−30b−30c=0.
But we can multiply through by 3:
9bc−30b−30c=0.
DPatrick
2015-02-26 19:54:57
Now 9bc=3b⋅3c is a symmetric factorization. Can we apply SFFT?
Now 9bc=3b⋅3c is a symmetric factorization. Can we apply SFFT?
pnpiano
2015-02-26 19:55:21
100
100
Deathranger999
2015-02-26 19:55:21
Add 100.
Add 100.
pnpiano
2015-02-26 19:55:21
add 100
add 100
droid347
2015-02-26 19:55:21
yes, add 100
yes, add 100
abean077
2015-02-26 19:55:21
(3b - 10)(3c - 10)
(3b - 10)(3c - 10)
jameswangisb
2015-02-26 19:55:21
(3b-10)(3c-10)=100
(3b-10)(3c-10)=100
DPatrick
2015-02-26 19:55:26
Yes! Add 100:
9bc−30b−30c+100=100.
And now we can factor: (3b−10)(3c−10)=100.
Yes! Add 100:
9bc−30b−30c+100=100.
And now we can factor: (3b−10)(3c−10)=100.
DPatrick
2015-02-26 19:55:36
What are the integer solutions to this?
What are the integer solutions to this?
TheMagician
2015-02-26 19:56:06
b=5 and c=10
b=5 and c=10
Darn
2015-02-26 19:56:06
There is only 1 way that satisfies our bounds: (5,10)
There is only 1 way that satisfies our bounds: (5,10)
rjiang16
2015-02-26 19:56:06
(5,10) and that's it?
(5,10) and that's it?
ZekromReshiram
2015-02-26 19:56:06
5 ways to factor 100
5 ways to factor 100
RegretDragunity
2015-02-26 19:56:06
1*100 5*20 2*50 4*25 10*10
1*100 5*20 2*50 4*25 10*10
MathLearner01
2015-02-26 19:56:06
(5,10)
(5,10)
Not_a_Username
2015-02-26 19:56:06
(b,c)=(5,10)
(b,c)=(5,10)
DPatrick
2015-02-26 19:56:11
100 can be factored 5 ways: 10⋅10, 5⋅20, 4⋅25, 2⋅50, and 1⋅100.
100 can be factored 5 ways: 10⋅10, 5⋅20, 4⋅25, 2⋅50, and 1⋅100.
DPatrick
2015-02-26 19:56:35
But we need pairs of factors that are each 10 less than a multiple of 3. So only some of these work.
But we need pairs of factors that are each 10 less than a multiple of 3. So only some of these work.
DPatrick
2015-02-26 19:56:42
5⋅20 works, giving b=5 and c=10.
5⋅20 works, giving b=5 and c=10.
DPatrick
2015-02-26 19:56:56
2⋅50 also works, giving b=4 and c=20.
2⋅50 also works, giving b=4 and c=20.
nosaj
2015-02-26 19:57:10
4, 20 doesn't work because 4<5
4, 20 doesn't work because 4<5
meteor88
2015-02-26 19:57:13
but b is less than a
but b is less than a
abean077
2015-02-26 19:57:13
But 4 is too low, it has to be at least a
But 4 is too low, it has to be at least a
DPatrick
2015-02-26 19:57:16
...but wait, that second one doesn't actually work, since we need 5≤b≤c.
...but wait, that second one doesn't actually work, since we need 5≤b≤c.
DPatrick
2015-02-26 19:57:30
So there's only 1 more solution in the a=5 case.
So there's only 1 more solution in the a=5 case.
RBMS14
2015-02-26 19:57:39
The answer is 10
The answer is 10
crosby87
2015-02-26 19:57:39
10 solutions therefore B
10 solutions therefore B
problemsolver12
2015-02-26 19:57:39
10 total then?
10 total then?
nosaj
2015-02-26 19:57:39
Therefore answer is (B) 10.
Therefore answer is (B) 10.
mathcountsprep
2015-02-26 19:57:39
9+1=10 (B)
9+1=10 (B)
ryansong2002
2015-02-26 19:57:39
so only 10?
so only 10?
DPatrick
2015-02-26 19:57:42
That brings our total up to 10 overall across all the cases. Answer (B).
That brings our total up to 10 overall across all the cases. Answer (B).
DPatrick
2015-02-26 19:58:07
OK, I'm going to take a 4 minute break. We'll resume at :02 past the hour!
OK, I'm going to take a 4 minute break. We'll resume at :02 past the hour!
DPatrick
2015-02-26 20:02:02
Hi, we're back!
Hi, we're back!
DPatrick
2015-02-26 20:02:15
We did 12B #21 (it was also 10B #21), so on to 12B #22:
We did 12B #21 (it was also 10B #21), so on to 12B #22:
DPatrick
2015-02-26 20:02:20
22. Six chairs are evenly spaced around a circular table. One person is seated in each chair. Each person gets up and sits down in a chair that is not the same chair and is not adjacent to the chair he or she originally occupied, so that again one person is seated in each chair. In how many ways can this be done?
12B:22
(A) 14(B) 16(C) 18(D) 20(E) 24
22. Six chairs are evenly spaced around a circular table. One person is seated in each chair. Each person gets up and sits down in a chair that is not the same chair and is not adjacent to the chair he or she originally occupied, so that again one person is seated in each chair. In how many ways can this be done?
12B:22
(A) 14(B) 16(C) 18(D) 20(E) 24
trumpeter
2015-02-26 20:02:44
casework!
casework!
rjiang16
2015-02-26 20:02:44
You can draw a tree map and count all 20 cases that work xD
You can draw a tree map and count all 20 cases that work xD
nosyarg
2015-02-26 20:02:44
cases?
cases?
abean077
2015-02-26 20:02:54
This looks like a caswework problem
This looks like a caswework problem
Satyaprakash2009rta
2015-02-26 20:02:54
cases
cases
DPatrick
2015-02-26 20:02:56
You can solve this directly by careful casework, as I did when I first attempted the problem, but it's a little messy.
You can solve this directly by careful casework, as I did when I first attempted the problem, but it's a little messy.
DPatrick
2015-02-26 20:03:07
Afterwards, my colleague Jeremy Copeland showed me a clever trick to make the problem a lot simpler.
Afterwards, my colleague Jeremy Copeland showed me a clever trick to make the problem a lot simpler.
DPatrick
2015-02-26 20:03:21
You can recast the problem as a 2-step process:
First, everyone gets up and sits in the chair immediately opposite them.
Second, everyone either stays put, or moves to the chair to their immediate left or right.
You can recast the problem as a 2-step process:
First, everyone gets up and sits in the chair immediately opposite them.
Second, everyone either stays put, or moves to the chair to their immediate left or right.
DPatrick
2015-02-26 20:03:42
Is it clear that this is exactly the same result as the original problem?
Is it clear that this is exactly the same result as the original problem?
DPatrick
2015-02-26 20:03:55
And since there are no choices in the first step, we just have to count the number of ways to do the second step.
And since there are no choices in the first step, we just have to count the number of ways to do the second step.
DPatrick
2015-02-26 20:04:10
So we can recast the problem as problem 22J:
So we can recast the problem as problem 22J:
DPatrick
2015-02-26 20:04:14
22J. Six chairs are evenly spaced around a circular table. One person is seated in each chair. Some people (perhaps none) get up and sit down in an adjacent chair, so that again one person is seated in each chair. In how many ways can this be done?
12B:22
(A) 14(B) 16(C) 18(D) 20(E) 24
22J. Six chairs are evenly spaced around a circular table. One person is seated in each chair. Some people (perhaps none) get up and sit down in an adjacent chair, so that again one person is seated in each chair. In how many ways can this be done?
12B:22
(A) 14(B) 16(C) 18(D) 20(E) 24
MSTang
2015-02-26 20:04:30
J for Jeremy?
J for Jeremy?
DPatrick
2015-02-26 20:04:33
Of course!
Of course!
DPatrick
2015-02-26 20:04:42
What are the possibilities? Are there any "obvious" possibilities that we can get out of the way right up front?
What are the possibilities? Are there any "obvious" possibilities that we can get out of the way right up front?
AMN300
2015-02-26 20:04:58
no one moves
no one moves
willalphagamma
2015-02-26 20:04:58
Everyone stays put
Everyone stays put
Frinkahedron
2015-02-26 20:04:58
everyone stays put
everyone stays put
Imagineny1
2015-02-26 20:04:58
all stay seated
all stay seated
az_phx_brandon_jiang
2015-02-26 20:04:58
No one moves again
No one moves again
DPatrick
2015-02-26 20:05:02
Everyone could just stay put. That's 1 possible outcome.
Everyone could just stay put. That's 1 possible outcome.
Tuxianeer
2015-02-26 20:05:15
everyone moves left/right
everyone moves left/right
Darn
2015-02-26 20:05:15
Rotate 1 to right or left
Rotate 1 to right or left
abean077
2015-02-26 20:05:15
Everyone shifts one space (counter)clockwise
Everyone shifts one space (counter)clockwise
ninjataco
2015-02-26 20:05:15
everyone moves 1 right or 1 left
everyone moves 1 right or 1 left
noobynoob
2015-02-26 20:05:15
everyone sits to the right or left
everyone sits to the right or left
chenmeister22
2015-02-26 20:05:15
everyone moves to the left or right
everyone moves to the left or right
ZekromReshiram
2015-02-26 20:05:15
Everyone moves to the left or right
Everyone moves to the left or right
DPatrick
2015-02-26 20:05:21
Or, everyone could move one seat to their left. That's another possible outcome.
Or, everyone could move one seat to their right. That's a third possible outcome.
Or, everyone could move one seat to their left. That's another possible outcome.
Or, everyone could move one seat to their right. That's a third possible outcome.
DPatrick
2015-02-26 20:05:30
Otherwise, what has to happen?
Otherwise, what has to happen?
mathwrath
2015-02-26 20:05:49
Pairs of switching
Pairs of switching
ompatel99
2015-02-26 20:05:49
Or one group of two adjacent could switch places
Or one group of two adjacent could switch places
UrInvalid
2015-02-26 20:05:49
two people swap
two people swap
Imagineny1
2015-02-26 20:05:49
switching seats
switching seats
willalphagamma
2015-02-26 20:05:49
Some two people have to swap
Some two people have to swap
DPatrick
2015-02-26 20:06:30
Right. The only cases left to count are where 1, 2, or 3 pairs of neighboring people swap seats. (And the rest stay put.)
Right. The only cases left to count are where 1, 2, or 3 pairs of neighboring people swap seats. (And the rest stay put.)
SimonSun
2015-02-26 20:06:50
1 swap is 6 ways
1 swap is 6 ways
DPatrick
2015-02-26 20:07:06
Right: if just one pair of people swap, there are 6 ways: just pick the pair of neighboring people to swap. (Alternatively, just pick a single person to move left; his neighbor to the left must then move right.)
Right: if just one pair of people swap, there are 6 ways: just pick the pair of neighboring people to swap. (Alternatively, just pick a single person to move left; his neighbor to the left must then move right.)
DPatrick
2015-02-26 20:07:13
In how many ways can 2 pairs of people swap?
In how many ways can 2 pairs of people swap?
MSTang
2015-02-26 20:07:59
6 + 3 = 9
6 + 3 = 9
UrInvalid
2015-02-26 20:07:59
6*3/2=9 ways
6*3/2=9 ways
DPatrick
2015-02-26 20:08:20
Right. There are 6 ways to pick a first pair (an example choice is in red below), and then 3 ways to pick a second pair (the blue choices below):
Right. There are 6 ways to pick a first pair (an example choice is in red below), and then 3 ways to pick a second pair (the blue choices below):
DPatrick
2015-02-26 20:08:25

DPatrick
2015-02-26 20:08:35
But this double-counts, since we could have chosen the pairs in either order. So there are (6*3)/2 = 9 possibilities in this case.
But this double-counts, since we could have chosen the pairs in either order. So there are (6*3)/2 = 9 possibilities in this case.
DPatrick
2015-02-26 20:09:03
Or, you could count the way to pick the two people who stay put: they are either neighbors (6 ways) or opposite each other (3 ways), for 6+3 = 9 total ways.
Or, you could count the way to pick the two people who stay put: they are either neighbors (6 ways) or opposite each other (3 ways), for 6+3 = 9 total ways.
DPatrick
2015-02-26 20:09:12
Finally, in how many ways can 3 pairs of people swap seats?
Finally, in how many ways can 3 pairs of people swap seats?
AMN300
2015-02-26 20:09:29
2 ways for 3 pairs to swap also
2 ways for 3 pairs to swap also
SimonSun
2015-02-26 20:09:29
3 swap is 2 choices
3 swap is 2 choices
ingridzhang97
2015-02-26 20:09:29
2 ways
2 ways
sparkles257
2015-02-26 20:09:29
2 ways to do 3 people
2 ways to do 3 people
ScottBusche
2015-02-26 20:09:29
2.
2.
Hydroxide
2015-02-26 20:09:29
2
2
TheStrangeCharm
2015-02-26 20:09:29
2
2
az_phx_brandon_jiang
2015-02-26 20:09:29
2 ways
2 ways
RegretDragunity
2015-02-26 20:09:29
2
2
DPatrick
2015-02-26 20:09:33
Just 2: either all the red pairs swap, or all the blue pairs swap:
Just 2: either all the red pairs swap, or all the blue pairs swap:
DPatrick
2015-02-26 20:09:38

SimonSun
2015-02-26 20:10:01
so it is (D) 20
so it is (D) 20
DPatrick
2015-02-26 20:10:04
Adding the different cases, we get 3 + 6 + 9 + 2 = 20 possibilities. Answer (D).
Adding the different cases, we get 3 + 6 + 9 + 2 = 20 possibilities. Answer (D).
DPatrick
2015-02-26 20:10:58
Again, you certainly could have counted the possibilities from the original problem directly, as I did when I first solved the problem, but it's a lot messier than this nice solution Jeremy came up with!
Again, you certainly could have counted the possibilities from the original problem directly, as I did when I first solved the problem, but it's a lot messier than this nice solution Jeremy came up with!
DPatrick
2015-02-26 20:11:17
We already did 12B #23 as 10B #25, so on to 12B #24:
We already did 12B #23 as 10B #25, so on to 12B #24:
DPatrick
2015-02-26 20:11:20
24. Four circles, no two of which are congruent, have centers at A, B, C, and D, and points P and Q lie on all four circles. The radius of circle A is 58 times the radius of circle B, and the radius of circle C is 58 times the radius of circle D. Furthermore, AB=CD=39 and PQ=48. Let R be the midpoint of ¯PQ. What is AR+BR+CR+DR?
12B:24
(A) 180(B) 184(C) 188(D) 192(E) 196
24. Four circles, no two of which are congruent, have centers at A, B, C, and D, and points P and Q lie on all four circles. The radius of circle A is 58 times the radius of circle B, and the radius of circle C is 58 times the radius of circle D. Furthermore, AB=CD=39 and PQ=48. Let R be the midpoint of ¯PQ. What is AR+BR+CR+DR?
12B:24
(A) 180(B) 184(C) 188(D) 192(E) 196
SimonSun
2015-02-26 20:11:47
draw it
draw it
nosyarg
2015-02-26 20:11:47
lets draw a picture
lets draw a picture
DPatrick
2015-02-26 20:11:50
It's hard to draw a picture of this...
It's hard to draw a picture of this...
DPatrick
2015-02-26 20:11:54
We don't really know where A, B, C, and D are.
We don't really know where A, B, C, and D are.
DPatrick
2015-02-26 20:12:03
What do we know about them?
What do we know about them?
trumpeter
2015-02-26 20:12:22
the four are collinear
the four are collinear
noobynoob
2015-02-26 20:12:22
collinear
collinear
ScottBusche
2015-02-26 20:12:22
They're collinear.
They're collinear.
swirlykick
2015-02-26 20:12:27
ABCD are colinear
ABCD are colinear
DPatrick
2015-02-26 20:12:37
More specifically, what line to they all lie on?
More specifically, what line to they all lie on?
giftedbee
2015-02-26 20:13:01
The perpendicular bisector of PQ
The perpendicular bisector of PQ
UrInvalid
2015-02-26 20:13:01
the perpendicular bisector of PQ
the perpendicular bisector of PQ
celery2
2015-02-26 20:13:01
perpendicular bisector of PQ
perpendicular bisector of PQ
DPatrick
2015-02-26 20:13:07
Right. If a circle passes through P and Q, then its center has to lie on the perpendicular bisector of ¯PQ. So A, B, C, D all lie on this line (which also passes through R).
Right. If a circle passes through P and Q, then its center has to lie on the perpendicular bisector of ¯PQ. So A, B, C, D all lie on this line (which also passes through R).
DPatrick
2015-02-26 20:13:29
From here there are some different approaches we can take. One that works nicely is to imagine this all on the coordinate plane.
From here there are some different approaches we can take. One that works nicely is to imagine this all on the coordinate plane.
DPatrick
2015-02-26 20:13:40
We probably want R to be the origin, and let's set it up so that ¯PQ lies along the y-axis. Something like this:
We probably want R to be the origin, and let's set it up so that ¯PQ lies along the y-axis. Something like this:
DPatrick
2015-02-26 20:13:45

DPatrick
2015-02-26 20:14:03
Warning: this picture might not be accurate! Note that A, B, C, and D all lie on the x-axis, but A and B might not be on the same side like I drew it above.
Warning: this picture might not be accurate! Note that A, B, C, and D all lie on the x-axis, but A and B might not be on the same side like I drew it above.
DPatrick
2015-02-26 20:14:13
But it's a place to start.
But it's a place to start.
DPatrick
2015-02-26 20:14:34
Also we notice that A,B and C,D have identical conditions but are themselves completely separate from each other. So let's try to solve for A,B first, and hopefully we'll actually get two solutions: one will be A,B and the other will be C,D.
Also we notice that A,B and C,D have identical conditions but are themselves completely separate from each other. So let's try to solve for A,B first, and hopefully we'll actually get two solutions: one will be A,B and the other will be C,D.
DPatrick
2015-02-26 20:15:06
So if R is the origin, then what are P are Q?
So if R is the origin, then what are P are Q?
UrInvalid
2015-02-26 20:15:34
(0,24)and(0,-24)
(0,24)and(0,-24)
acegikmoqsuwy2000
2015-02-26 20:15:34
(0,24) and (0,-24)
(0,24) and (0,-24)
Imagineny1
2015-02-26 20:15:34
(0,24) (0, -24)
(0,24) (0, -24)
ingridzhang97
2015-02-26 20:15:34
(0,24) and (0,-24
(0,24) and (0,-24
pnpiano
2015-02-26 20:15:34
(0,24) and (0,-24)
(0,24) and (0,-24)
eswa2000
2015-02-26 20:15:34
(0,24), (0,-24)
(0,24), (0,-24)
AMN300
2015-02-26 20:15:34
(0, 24) and (0, -24)
(0, 24) and (0, -24)
az_phx_brandon_jiang
2015-02-26 20:15:39
(0,24) and (0,-24)
(0,24) and (0,-24)
DPatrick
2015-02-26 20:15:51
Right. P is (0,24) and Q is (0,−24).
Right. P is (0,24) and Q is (0,−24).
DPatrick
2015-02-26 20:16:00
We can also set A to be (x,0) for some x. Then what's B?
We can also set A to be (x,0) for some x. Then what's B?
Imagineny1
2015-02-26 20:16:24
(x+39,0)
(x+39,0)
Amrutamaya
2015-02-26 20:16:24
x+39,0
x+39,0
AMN300
2015-02-26 20:16:24
(x+39, 0) or (x-39, 0)
(x+39, 0) or (x-39, 0)
mathperson9
2015-02-26 20:16:24
(x+39,0)
(x+39,0)
hnkevin42
2015-02-26 20:16:24
(x + 39, 0)
(x + 39, 0)
ingridzhang97
2015-02-26 20:16:24
(x+39,0)
(x+39,0)
DPatrick
2015-02-26 20:16:27
Then since AB=39 we have B=(x+39,0). (Note that we can assume that B is to the right of A by symmetry; if not, just reflect it across the y-axis.)
Then since AB=39 we have B=(x+39,0). (Note that we can assume that B is to the right of A by symmetry; if not, just reflect it across the y-axis.)
DPatrick
2015-02-26 20:16:38
So we've got this:
So we've got this:
DPatrick
2015-02-26 20:16:42
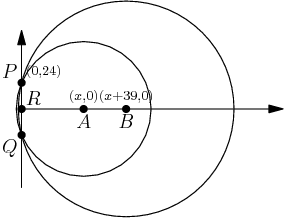

DPatrick
2015-02-26 20:16:47
Now what?
Now what?
Satyaprakash2009rta
2015-02-26 20:17:02
ratio of radius
ratio of radius
nosaj
2015-02-26 20:17:02
solve for the radius
solve for the radius
AMN300
2015-02-26 20:17:14
We need to use the radius length condition
We need to use the radius length condition
RahulKrishnan
2015-02-26 20:17:14
solve for radius
solve for radius
DPatrick
2015-02-26 20:17:17
We're given that AP=58⋅BP, or 8(AP)=5(BP).
We're given that AP=58⋅BP, or 8(AP)=5(BP).
DivideBy0
2015-02-26 20:17:26
use pythag on radius
use pythag on radius
DPatrick
2015-02-26 20:17:37
Right, we can compute AP and BP using our coordinates!
Right, we can compute AP and BP using our coordinates!
DPatrick
2015-02-26 20:17:47
Squaring first, though, seems like a sensible thing to do: 64(AP)2=25(BP)2.
Squaring first, though, seems like a sensible thing to do: 64(AP)2=25(BP)2.
DPatrick
2015-02-26 20:18:01
(No nasty square roots to deal with now.)
(No nasty square roots to deal with now.)
DPatrick
2015-02-26 20:18:08
Now we just plug in the formulas for the distances:
64(x2+242)=25((x+39)2+242).
Now we just plug in the formulas for the distances:
64(x2+242)=25((x+39)2+242).
EulerMacaroni
2015-02-26 20:18:33
that's an ugly quadratic
that's an ugly quadratic
SimonSun
2015-02-26 20:18:33
too big
too big
Darn
2015-02-26 20:18:33
Rearrange
Rearrange
DPatrick
2015-02-26 20:18:42
This simplifies (if you can call it that) to 39x2−50(39)x+(39(242)−25(392))=0.
This simplifies (if you can call it that) to 39x2−50(39)x+(39(242)−25(392))=0.
ingridzhang97
2015-02-26 20:19:00
divide by 39
divide by 39
EulerMacaroni
2015-02-26 20:19:00
Factor out a 39
Factor out a 39
mathtastic
2015-02-26 20:19:00
DIVIDE BY 39!!
DIVIDE BY 39!!
dli00105
2015-02-26 20:19:00
divide by 39
divide by 39
numbersandnumbers
2015-02-26 20:19:00
divide by 39
divide by 39
DPatrick
2015-02-26 20:19:04
How convenient! We can divide by 39 to get just x2−50x−399=0.
How convenient! We can divide by 39 to get just x2−50x−399=0.
DPatrick
2015-02-26 20:19:12
399 = 3 * 7 * 19, so can you see how it factors?
399 = 3 * 7 * 19, so can you see how it factors?
bharatputra
2015-02-26 20:19:40
x=57 or -7 but only 57 works
x=57 or -7 but only 57 works
Tuxianeer
2015-02-26 20:19:40
57,-7
57,-7
ninjataco
2015-02-26 20:19:40
(x-57)(x+7)
(x-57)(x+7)
sssssssssssssss
2015-02-26 20:19:40
x-57, x+7
x-57, x+7
celery2
2015-02-26 20:19:40
(x-57)(x+7)=0
(x-57)(x+7)=0
DPatrick
2015-02-26 20:19:44
It factors as (x−57)(x+7)=0.
It factors as (x−57)(x+7)=0.
DPatrick
2015-02-26 20:19:49
And, as hoped, we get two solutions: x=57 and x=−7.
And, as hoped, we get two solutions: x=57 and x=−7.
DPatrick
2015-02-26 20:20:10
Of course, my picture doesn't match the x=−7 case, but that doesn't matter, because all the algebra works just fine!
Of course, my picture doesn't match the x=−7 case, but that doesn't matter, because all the algebra works just fine!
DPatrick
2015-02-26 20:20:26
So one pair of circles are centered at (57,0) and (96,0), and the other pair of circles are centered at (-7,0) and (32,0). (Up to reflection, of course -- the second pair might be at (7,0) and (-32,0), for instance.)
So one pair of circles are centered at (57,0) and (96,0), and the other pair of circles are centered at (-7,0) and (32,0). (Up to reflection, of course -- the second pair might be at (7,0) and (-32,0), for instance.)
DPatrick
2015-02-26 20:20:42
And what's the final answer?
And what's the final answer?
celery2
2015-02-26 20:20:58
192
192
giftedbee
2015-02-26 20:20:58
D
D
mattpi
2015-02-26 20:20:58
D
D
abean077
2015-02-26 20:20:58
Now just add 57+96+7+32
Now just add 57+96+7+32
DPatrick
2015-02-26 20:21:04
We just sum the absolute values of the x-coordinates: 57+96+7+32 = 192. Answer (D).
We just sum the absolute values of the x-coordinates: 57+96+7+32 = 192. Answer (D).
DPatrick
2015-02-26 20:21:33
They were kind, I thought, not to put 178 as an answer choice, since 178 = 57 + 96 - 7 + 32 might be a common mistake.
They were kind, I thought, not to put 178 as an answer choice, since 178 = 57 + 96 - 7 + 32 might be a common mistake.
DPatrick
2015-02-26 20:21:53
I thought this was a cute problem.
I thought this was a cute problem.
DPatrick
2015-02-26 20:22:03
And on to 12B #25:
And on to 12B #25:
DPatrick
2015-02-26 20:22:09
25. A bee starts flying from point P0. She flies 1 inch due east to point P1. For j≥1, once the bee reaches point Pj, she turns 30∘ counterclockwise and then flies j+1 inches straight to point Pj+1. When the bee reaches P2015 she is exactly a√b+c√d inches away from P0, where a, b, c, and d are positive integers and b and d are not divisible by the square of any prime. What is a+b+c+d?
12B:25
(A) 2016(B) 2024(C) 2032(D) 2040(E) 2048
25. A bee starts flying from point P0. She flies 1 inch due east to point P1. For j≥1, once the bee reaches point Pj, she turns 30∘ counterclockwise and then flies j+1 inches straight to point Pj+1. When the bee reaches P2015 she is exactly a√b+c√d inches away from P0, where a, b, c, and d are positive integers and b and d are not divisible by the square of any prime. What is a+b+c+d?
12B:25
(A) 2016(B) 2024(C) 2032(D) 2040(E) 2048
DPatrick
2015-02-26 20:22:30
(I wonder why Aaron the ant got a name from the 10A problem, but this bee is anonymous. I'm going to call her Betty. And she can call me Al.)
(I wonder why Aaron the ant got a name from the 10A problem, but this bee is anonymous. I'm going to call her Betty. And she can call me Al.)
EulerMacaroni
2015-02-26 20:22:52
Complex numbers here
Complex numbers here
AMN300
2015-02-26 20:22:52
complex plane!
complex plane!
AMN300
2015-02-26 20:22:52
Since we are rotating, we could use the complex plane
Since we are rotating, we could use the complex plane
hnkevin42
2015-02-26 20:22:52
These rotations are making me want to use the complex numbers.
These rotations are making me want to use the complex numbers.
DPatrick
2015-02-26 20:23:18
Good idea! Trying to track this sort of rotational movement is a great candidate for using the complex plane.
Good idea! Trying to track this sort of rotational movement is a great candidate for using the complex plane.
DPatrick
2015-02-26 20:23:38
Let's set w=√32+12i=e(πi)/6 to be the complex number with |w|=1 that is along the 30∘ ray. Note that w is a primitive 12th root of unity, so that w12=1.
Let's set w=√32+12i=e(πi)/6 to be the complex number with |w|=1 that is along the 30∘ ray. Note that w is a primitive 12th root of unity, so that w12=1.
DPatrick
2015-02-26 20:23:57
The key fact is that rotating by 30∘ is the same as multiplying by w.
The key fact is that rotating by 30∘ is the same as multiplying by w.
DPatrick
2015-02-26 20:24:38
(I should warn you -- if you haven't yet seen this sort of math before, you're probably going to be mostly lost in this problem. See what you can pick up, and I'm going to do a couple more AMC 10 problems after this one.)
(I should warn you -- if you haven't yet seen this sort of math before, you're probably going to be mostly lost in this problem. See what you can pick up, and I'm going to do a couple more AMC 10 problems after this one.)
DPatrick
2015-02-26 20:25:05
So on move k, what complex number are we adding to Betty's position?
So on move k, what complex number are we adding to Betty's position?
MSTang
2015-02-26 20:25:34
kwk−1
kwk−1
trumpeter
2015-02-26 20:25:34
kwk−1
kwk−1
mathtastic
2015-02-26 20:25:39
kwk−1
kwk−1
DPatrick
2015-02-26 20:25:48
Good. On move k, we are moving along the direction kwk−1, and "moving" means adding kwk−1 to our current position.
Good. On move k, we are moving along the direction kwk−1, and "moving" means adding kwk−1 to our current position.
DPatrick
2015-02-26 20:26:07
(The first move is 1, the second move is 2w, the third move is 3w2, and so on.)
(The first move is 1, the second move is 2w, the third move is 3w2, and so on.)
mathtastic
2015-02-26 20:26:13
the answer is just |1+2w+3w2+⋯+2015w2014|
the answer is just |1+2w+3w2+⋯+2015w2014|
DPatrick
2015-02-26 20:26:19
Therefore, after 2015 moves, we're at the point
1+2w+3w2+4w3+⋯+2015w2014.
Let's call this number s. We want to compute |s|.
Therefore, after 2015 moves, we're at the point
1+2w+3w2+4w3+⋯+2015w2014.
Let's call this number s. We want to compute |s|.
UrInvalid
2015-02-26 20:26:33
arithmeto-geometric sequence
arithmeto-geometric sequence
ingridzhang97
2015-02-26 20:26:33
arithmetic-geometric sequence
arithmetic-geometric sequence
DPatrick
2015-02-26 20:26:53
Indeed, it looks a bit like a geometric series, and a bit like an arithmetic sequence...what's the standard technique we would use for this?
Indeed, it looks a bit like a geometric series, and a bit like an arithmetic sequence...what's the standard technique we would use for this?
dhruv
2015-02-26 20:27:19
multiply by ratio
multiply by ratio
az_phx_brandon_jiang
2015-02-26 20:27:19
multiply by w and subtract
multiply by w and subtract
ninjataco
2015-02-26 20:27:19
multiply s by w, and then subtract w from sw
multiply s by w, and then subtract w from sw
eswa2000
2015-02-26 20:27:19
multiply by w
multiply by w
DivideBy0
2015-02-26 20:27:19
multiply by w and subtract
multiply by w and subtract
DPatrick
2015-02-26 20:27:25
We multiply by the common ratio. So let's do that:
ws=w+2w2+3w3+⋯+2015w2015.
We multiply by the common ratio. So let's do that:
ws=w+2w2+3w3+⋯+2015w2015.
DPatrick
2015-02-26 20:27:33
And then subtracting makes it (almost) into an actual geometric sequence:
s=1+2w+3w2+4w3+⋯+2015w2014ws=1+w+2w2+3w3+⋯+2014w2014+2015w2015s−ws=1+2w+3w2+4w3+⋯+2015w2014−2015w2015.
We've got that extra term at the end that's annoying, but the rest is nice and geometric.
And then subtracting makes it (almost) into an actual geometric sequence:
s=1+2w+3w2+4w3+⋯+2015w2014ws=1+w+2w2+3w3+⋯+2014w2014+2015w2015s−ws=1+2w+3w2+4w3+⋯+2015w2014−2015w2015.
We've got that extra term at the end that's annoying, but the rest is nice and geometric.
DPatrick
2015-02-26 20:27:49
How can we make the geometric series part even nicer?
How can we make the geometric series part even nicer?
mathtastic
2015-02-26 20:28:10
Well now let's simplify 1+w+w2+⋯+w2014
Well now let's simplify 1+w+w2+⋯+w2014
bharatputra
2015-02-26 20:28:16
w^2015-1/w-1
w^2015-1/w-1
ninjataco
2015-02-26 20:28:16
write it as (w^2015 - 1)/(w-1)
write it as (w^2015 - 1)/(w-1)
AMN300
2015-02-26 20:28:16
(w^(2015)-1)/(w-1)
(w^(2015)-1)/(w-1)
DPatrick
2015-02-26 20:28:29
We could...but is there something we could do first that would be really really helpful?
We could...but is there something we could do first that would be really really helpful?
DPatrick
2015-02-26 20:28:42
Hint: 2016 is a multiple of 12!
Hint: 2016 is a multiple of 12!
DivideBy0
2015-02-26 20:29:08
add w^2015
add w^2015
mathwrath
2015-02-26 20:29:20
1+w+w^2+...+w^11 = 0
1+w+w^2+...+w^11 = 0
TheStrangeCharm
2015-02-26 20:29:20
we know that 1+ω+...+ω11=0
we know that 1+ω+...+ω11=0
Waley
2015-02-26 20:29:25
add w^2015 and subtract it away
add w^2015 and subtract it away
happiface
2015-02-26 20:29:25
subtract and add w^2015
subtract and add w^2015
DPatrick
2015-02-26 20:29:36
We can add a w2015 term to the geometric series, and subtract another one off in that "extra" term. That is,
s−ws=1+w+w2+⋯+w2014+w2015−2016w2015.
How does that help immensely?
We can add a w2015 term to the geometric series, and subtract another one off in that "extra" term. That is,
s−ws=1+w+w2+⋯+w2014+w2015−2016w2015.
How does that help immensely?
ninjataco
2015-02-26 20:29:59
the sum of the first 2016 terms is 0
the sum of the first 2016 terms is 0
trumpeter
2015-02-26 20:29:59
that geo series equals 0
that geo series equals 0
bharatputra
2015-02-26 20:29:59
the geometric series just becomes 0
the geometric series just becomes 0
celery2
2015-02-26 20:29:59
the front part is 0
the front part is 0
Satyaprakash2009rta
2015-02-26 20:29:59
sum of geometric series is 0
sum of geometric series is 0
DPatrick
2015-02-26 20:30:08
Now the geometric series part just sums to 0! If you prefer the formula, the sum is 1−w20161−w, and since 2016 is a multiple of 12, we have w2016=1, so this is just 0.
Now the geometric series part just sums to 0! If you prefer the formula, the sum is 1−w20161−w, and since 2016 is a multiple of 12, we have w2016=1, so this is just 0.
DPatrick
2015-02-26 20:30:20
So now we have simply s−ws=−2016w2015, and hence
s=2016w2015w−1.
So now we have simply s−ws=−2016w2015, and hence
s=2016w2015w−1.
DPatrick
2015-02-26 20:30:30
How do we compute |s| from this?
How do we compute |s| from this?
MSTang
2015-02-26 20:30:56
it equals 2016/magnitude(w-1)
it equals 2016/magnitude(w-1)
DPatrick
2015-02-26 20:31:00
Magnitude is multiplicative, so
|s|=|2016w2015w−1|=2016|w|2015|w−1|.
Magnitude is multiplicative, so
|s|=|2016w2015w−1|=2016|w|2015|w−1|.
dhruv
2015-02-26 20:31:08
|w|=1
|w|=1
DPatrick
2015-02-26 20:31:12
And we know |w|=1, so we have just |s|=2016|w−1|.
And we know |w|=1, so we have just |s|=2016|w−1|.
DPatrick
2015-02-26 20:31:20
And how do we compute |w−1|?
And how do we compute |w−1|?
MSTang
2015-02-26 20:31:47
w=√3/2+i/2
w=√3/2+i/2
sparkles257
2015-02-26 20:31:47
using w and finding mag normally
using w and finding mag normally
DPatrick
2015-02-26 20:31:53
One idea is that we know w=√32+12i, so we can just compute it directly:
w−1=(√32−1)+12i,
so
|w−1|2=(√32−1)2+(12)2.
One idea is that we know w=√32+12i, so we can just compute it directly:
w−1=(√32−1)+12i,
so
|w−1|2=(√32−1)2+(12)2.
DPatrick
2015-02-26 20:32:12
This computes to:
|w−1|2=(√3−2)2+14=8−4√34=2−√3.
This computes to:
|w−1|2=(√3−2)2+14=8−4√34=2−√3.
DPatrick
2015-02-26 20:32:22
So |w−1|=√2−√3. How do we compute this?
So |w−1|=√2−√3. How do we compute this?
brian22
2015-02-26 20:33:11
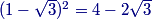
MSTang
2015-02-26 20:33:11
(√3−1)2=4−2√3
(√3−1)2=4−2√3
DPatrick
2015-02-26 20:33:21
Indeed, one clever way to continue is to recognize that
2−√3=4−2√32=(√3−1)22,
so that √2−√3=√3−1√2.
Indeed, one clever way to continue is to recognize that
2−√3=4−2√32=(√3−1)22,
so that √2−√3=√3−1√2.
DPatrick
2015-02-26 20:33:45
But that's kind of magical.
But that's kind of magical.
DPatrick
2015-02-26 20:33:56
Another approach, that avoids having to compute a square-root via magic, is to draw a picture:
Another approach, that avoids having to compute a square-root via magic, is to draw a picture:
DPatrick
2015-02-26 20:34:03

DPatrick
2015-02-26 20:34:17
The picture above is how we geometrically determine the location of w−1. The length |w−1| is the length of the black segment in the picture.
The picture above is how we geometrically determine the location of w−1. The length |w−1| is the length of the black segment in the picture.
DPatrick
2015-02-26 20:34:34
Notice it's the base of an isosceles triangle with legs of length 1 and vertex angle of 30∘.
Notice it's the base of an isosceles triangle with legs of length 1 and vertex angle of 30∘.
DPatrick
2015-02-26 20:34:47
So trig tells us...
So trig tells us...
mathtastic
2015-02-26 20:34:54
yeah just compute with sin15∘
yeah just compute with sin15∘
DPatrick
2015-02-26 20:35:07
So by dropping the altitude from the vertex to the base, we see that the length is 2sin15∘.
So by dropping the altitude from the vertex to the base, we see that the length is 2sin15∘.
DPatrick
2015-02-26 20:35:15
And how do we compute that?
And how do we compute that?
MSTang
2015-02-26 20:35:34
sin(45-30)
sin(45-30)
az_phx_brandon_jiang
2015-02-26 20:35:34
subtraction cause half angle is bad
subtraction cause half angle is bad
hnkevin42
2015-02-26 20:35:34
sine subtraction formula
sine subtraction formula
DrMath
2015-02-26 20:35:34
sin(45−30)
sin(45−30)
Waley
2015-02-26 20:35:44
sin15=sin(45-30) use angle subtraction law
sin15=sin(45-30) use angle subtraction law
sillyd
2015-02-26 20:35:44
sin(45-30)
sin(45-30)
DPatrick
2015-02-26 20:35:47
We can use the difference-angle formula for sine:
sin(45∘−30∘)=sin45∘cos30∘−sin30∘cos45∘.
We can use the difference-angle formula for sine:
sin(45∘−30∘)=sin45∘cos30∘−sin30∘cos45∘.
DPatrick
2015-02-26 20:35:53
Thus
sin15∘=√3−12√2,
and |w−1|=2sin15∘=√3−1√2, just as before.
Thus
sin15∘=√3−12√2,
and |w−1|=2sin15∘=√3−1√2, just as before.
DPatrick
2015-02-26 20:36:17
Anyway, to finish, our answer is
|s|=2016|w−1|=2016√2√3−1.
Anyway, to finish, our answer is
|s|=2016|w−1|=2016√2√3−1.
sparkles257
2015-02-26 20:36:48
rationalize!
rationalize!
acegikmoqsuwy2000
2015-02-26 20:36:48
rationalize denominator
rationalize denominator
sharmag
2015-02-26 20:36:48
rationalize denominator?
rationalize denominator?
eswa2000
2015-02-26 20:36:48
rationalize the denom
rationalize the denom
ninjataco
2015-02-26 20:36:48
multiply numerator and denominator by (sqrt3 + 1)
multiply numerator and denominator by (sqrt3 + 1)
happiface
2015-02-26 20:36:48
they want us to rationalize more apparently
they want us to rationalize more apparently
DPatrick
2015-02-26 20:36:59
We need square roots in our answer and no denominators.
We need square roots in our answer and no denominators.
DPatrick
2015-02-26 20:37:04
We rationalize the denominator by multiplying through by √3+1:
|s|=2016√2(√3+1)(√3−1)(√3+1)=2016(√6+√2)2=1008√6+1008√2.
We rationalize the denominator by multiplying through by √3+1:
|s|=2016√2(√3+1)(√3−1)(√3+1)=2016(√6+√2)2=1008√6+1008√2.
alex7
2015-02-26 20:37:26
that equals 1008+6+1008+2=2024
that equals 1008+6+1008+2=2024
ingridzhang97
2015-02-26 20:37:26
so answer is B) 2024
so answer is B) 2024
Darn
2015-02-26 20:37:26
1008+6+1008+2=B
1008+6+1008+2=B
DPatrick
2015-02-26 20:37:28
Thus our final answer is 1008+6+1008+2 = 2024. Answer (B).
Thus our final answer is 1008+6+1008+2 = 2024. Answer (B).
droid347
2015-02-26 20:37:52
Can we do 10B #19 now pleaseee?
Can we do 10B #19 now pleaseee?
DPatrick
2015-02-26 20:38:05
Yeah, we've got a little more time, so let's do #19, which happened to be the same on both contests.
Yeah, we've got a little more time, so let's do #19, which happened to be the same on both contests.
DPatrick
2015-02-26 20:38:11
19. In △ABC, ∠C=90∘ and AB=12. Squares ABXY and ACWZ are constructed outside of the triangle. The points X, Y, Z, and W lie on a circle. What is the perimeter of the triangle?
19B
(A) 12+9√3 (B) 18+6√3 (C) 12+12√2 (D) 30 (E) 32
19. In △ABC, ∠C=90∘ and AB=12. Squares ABXY and ACWZ are constructed outside of the triangle. The points X, Y, Z, and W lie on a circle. What is the perimeter of the triangle?
19B
(A) 12+9√3 (B) 18+6√3 (C) 12+12√2 (D) 30 (E) 32
DPatrick
2015-02-26 20:38:31
Here we can sketch a reasonable picture:
Here we can sketch a reasonable picture:
DPatrick
2015-02-26 20:38:36
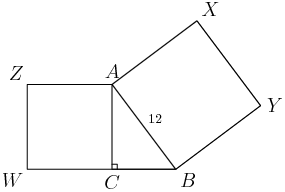

DPatrick
2015-02-26 20:38:49
The other condition is that X, Y, Z, and W all lie on a circle. Where does the center of that circle have to be?
The other condition is that X, Y, Z, and W all lie on a circle. Where does the center of that circle have to be?
AMN300
2015-02-26 20:39:17
Midpoint of AB
Midpoint of AB
sparkles257
2015-02-26 20:39:17
center of circle is midpt.of AB
center of circle is midpt.of AB
noobynoob
2015-02-26 20:39:17
midpoint of AB
midpoint of AB
EulerMacaroni
2015-02-26 20:39:17
The midpoint of ¯AB
The midpoint of ¯AB
BobaFett101
2015-02-26 20:39:17
midpoint of AB
midpoint of AB
gurev
2015-02-26 20:39:17
midpoint of AB
midpoint of AB
Deathranger999
2015-02-26 20:39:17
The midpoint of the hypotenuse.
The midpoint of the hypotenuse.
brian22
2015-02-26 20:39:17
bisectory of WZ intersected with bisector of XY
bisectory of WZ intersected with bisector of XY
vinayak-kumar
2015-02-26 20:39:17
Intersection of perpendicular bisctors
Intersection of perpendicular bisctors
DPatrick
2015-02-26 20:39:28
Any circle containing X and Y has its center on the perpendicular bisector of ¯XY. This is the same as the perpendicular bisector of ¯AB.
Any circle containing X and Y has its center on the perpendicular bisector of ¯XY. This is the same as the perpendicular bisector of ¯AB.
DPatrick
2015-02-26 20:39:36
Any circle containing Z and W has its center on the perpendicular bisector of ¯WZ. This is the same as the perpendicular bisector of ¯AC.
Any circle containing Z and W has its center on the perpendicular bisector of ¯WZ. This is the same as the perpendicular bisector of ¯AC.
DPatrick
2015-02-26 20:40:01
But the perpendicular bisector of ¯AC is parallel to ¯CB, so it creates a triangle similar to ABC but half the size.
But the perpendicular bisector of ¯AC is parallel to ¯CB, so it creates a triangle similar to ABC but half the size.
DPatrick
2015-02-26 20:40:19
Thus, it interescts ¯AB at the midpoint of ¯AB! Let's call that point O. That's the center of the circle.
Thus, it interescts ¯AB at the midpoint of ¯AB! Let's call that point O. That's the center of the circle.
DPatrick
2015-02-26 20:40:31
From this, can we determine the radius of the circle?
From this, can we determine the radius of the circle?
mathperson9
2015-02-26 20:40:55
Which is 6\sqrt{5} from X, Y, Z, and W
Which is 6\sqrt{5} from X, Y, Z, and W
DivideBy0
2015-02-26 20:40:55
pythag!
pythag!
CountDown
2015-02-26 20:40:55
yes, it's 6sqrt5
yes, it's 6sqrt5
EulerMacaroni
2015-02-26 20:40:55
6√5
6√5
mathperson9
2015-02-26 20:40:55
OZ is 6\Sqrt{5}
OZ is 6\Sqrt{5}
DPatrick
2015-02-26 20:40:58
Sure: we can just look at triangle OBY:
Sure: we can just look at triangle OBY:
DPatrick
2015-02-26 20:41:03
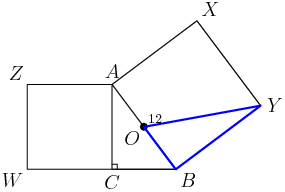

DPatrick
2015-02-26 20:41:17
We have OB=6 and BY=12, so by the Pythagorean Theorem OY=√62+122=6√5 is the radius.
We have OB=6 and BY=12, so by the Pythagorean Theorem OY=√62+122=6√5 is the radius.
Darn
2015-02-26 20:41:32
Then find distance to Z or W!
Then find distance to Z or W!
DrMath
2015-02-26 20:41:35
so we can use that to make an equation for OZ
so we can use that to make an equation for OZ
DPatrick
2015-02-26 20:41:45
Right. We can compute OZ=6√5 in a similar fashion. But we'll need to name some lengths.
Right. We can compute OZ=6√5 in a similar fashion. But we'll need to name some lengths.
DPatrick
2015-02-26 20:41:51
Let BC=a and AC=b, and consider OPZ as shown below:
Let BC=a and AC=b, and consider OPZ as shown below:
DPatrick
2015-02-26 20:41:55
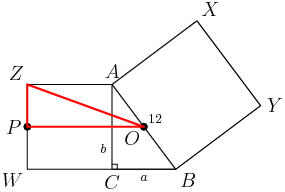

DPatrick
2015-02-26 20:42:04
What are OP and ZP?
What are OP and ZP?
EulerMacaroni
2015-02-26 20:42:31
OP is b+a/2
OP is b+a/2
donot
2015-02-26 20:42:31
b+a2
b+a2
bharatputra
2015-02-26 20:42:31
b+a/2 and b/2
b+a/2 and b/2
TheStrangeCharm
2015-02-26 20:42:31
b + a\2 and b/2
b + a\2 and b/2
akaashp11
2015-02-26 20:42:31
OP=a/2+b
OP=a/2+b
ingridzhang97
2015-02-26 20:42:31
OP=b+a/2, ZP=b/2
OP=b+a/2, ZP=b/2
DominicanAOPSer
2015-02-26 20:42:31
OP = b + a/2
OP = b + a/2
CountDown
2015-02-26 20:42:31
b/2, b + a/2
b/2, b + a/2
DPatrick
2015-02-26 20:42:38
Right. OP=a2+b and PZ=b2.
Right. OP=a2+b and PZ=b2.
DPatrick
2015-02-26 20:42:48
So the Pythagorean Theorem on OPZ gives us
(a2+b)2+(b2)2=(6√5)2.
So the Pythagorean Theorem on OPZ gives us
(a2+b)2+(b2)2=(6√5)2.
EulerMacaroni
2015-02-26 20:43:09
but multiply through by 4 here so its not ugly
but multiply through by 4 here so its not ugly
DPatrick
2015-02-26 20:43:16
Good idea. Multiplying through by 4 gives
(a+2b)2+b2=720,
or a2+4ab+5b2=720.
Good idea. Multiplying through by 4 gives
(a+2b)2+b2=720,
or a2+4ab+5b2=720.
happiface
2015-02-26 20:43:26
But we also have that a2+b2=144 from the triangle ABC.
But we also have that a2+b2=144 from the triangle ABC.
droid347
2015-02-26 20:43:26
but a2+b2=144
but a2+b2=144
DPatrick
2015-02-26 20:43:33
Right, they're the sides of the original triangle, so a2+b2=144.
Right, they're the sides of the original triangle, so a2+b2=144.
DPatrick
2015-02-26 20:43:53
Subtracting this from our other equation gives 4ab+4b2=720−144=576.
Subtracting this from our other equation gives 4ab+4b2=720−144=576.
thequantumguy
2015-02-26 20:44:22
divide by 4
divide by 4
DPatrick
2015-02-26 20:44:25
And now dividing by 4 again gives ab+b2=144.
And now dividing by 4 again gives ab+b2=144.
DPatrick
2015-02-26 20:44:32
But we also just had a2+b2=144.
But we also just had a2+b2=144.
noobynoob
2015-02-26 20:44:44
a=b
a=b
EulerMacaroni
2015-02-26 20:44:44
ab=a2
ab=a2
RJ810
2015-02-26 20:44:44
a=b
a=b
AMN300
2015-02-26 20:44:44
Hence a=b !
Hence a=b !
NewbieGamer
2015-02-26 20:44:44
a=b
a=b
DPatrick
2015-02-26 20:44:53
So we must have ab=a2, or b=a.
So we must have ab=a2, or b=a.
DPatrick
2015-02-26 20:44:59
So the original right triangle ABC is isosceles. How do we finish the problem?
So the original right triangle ABC is isosceles. How do we finish the problem?
dli00105
2015-02-26 20:45:16
a=b=6\sqrt{2}
a=b=6\sqrt{2}
sparkles257
2015-02-26 20:45:16
a= 6sqrt(2) = b
a= 6sqrt(2) = b
uniqueearth
2015-02-26 20:45:16
a=b=6sqrt2
a=b=6sqrt2
AMN300
2015-02-26 20:45:16
So a=b=6 sqrt 2 by 45-45-90, so we have an answer of C after adding
So a=b=6 sqrt 2 by 45-45-90, so we have an answer of C after adding
MathLearner01
2015-02-26 20:45:24
12+12sqrt2
12+12sqrt2
alex7
2015-02-26 20:45:24
12+6sqrt2*2
12+6sqrt2*2
acegikmoqsuwy2000
2015-02-26 20:45:24
12+6sqrt2+6sqrt2 = 12+12sqrt2 so (C)
12+6sqrt2+6sqrt2 = 12+12sqrt2 so (C)
DPatrick
2015-02-26 20:45:27
If AB=12 and ABC is right isosceles, then AC=BC=6√2. So its perimeter is 12+12√2, answer (C).
If AB=12 and ABC is right isosceles, then AC=BC=6√2. So its perimeter is 12+12√2, answer (C).
DPatrick
2015-02-26 20:45:59
Let's quickly do both #20's before calling it a night. One is sorta interesting, and one is really not.
Let's quickly do both #20's before calling it a night. One is sorta interesting, and one is really not.
DPatrick
2015-02-26 20:46:07
First, the 10B #20:
First, the 10B #20:
DPatrick
2015-02-26 20:46:11
20. Erin the ant starts at a given corner of a cube and crawls along exactly 7 edges in such a way that she visits every corner exactly once and then finds that she is unable to return along an edge to her starting point. How many paths are there meeting these conditions?
20B
(A) 6 (B) 9 (C) 12 (D) 18 (E) 24
20. Erin the ant starts at a given corner of a cube and crawls along exactly 7 edges in such a way that she visits every corner exactly once and then finds that she is unable to return along an edge to her starting point. How many paths are there meeting these conditions?
20B
(A) 6 (B) 9 (C) 12 (D) 18 (E) 24
DPatrick
2015-02-26 20:46:41
Heh. Erin the ant in #20, and Aaron the ant in #24. I just noticed that.
Heh. Erin the ant in #20, and Aaron the ant in #24. I just noticed that.
Darn
2015-02-26 20:47:14
Notice that by parity, we can only have the diagonally opposite corner as our end of the path
Notice that by parity, we can only have the diagonally opposite corner as our end of the path
fluffyanimal
2015-02-26 20:47:14
There are 6 ways to do the first 2 steps which are all the same
There are 6 ways to do the first 2 steps which are all the same
DPatrick
2015-02-26 20:47:32
That's a really key observation for this problem: the first two moves don't matter.
That's a really key observation for this problem: the first two moves don't matter.
DPatrick
2015-02-26 20:47:39
All 3 choices for the first move are symmetric.
All 3 choices for the first move are symmetric.
DPatrick
2015-02-26 20:47:54
And then for the second move, there are 2 choices, but both lead to a corner that's opposite (across a face) from the starting point.
And then for the second move, there are 2 choices, but both lead to a corner that's opposite (across a face) from the starting point.
DPatrick
2015-02-26 20:48:01
So the first 3⋅2=6 possible pairs of first moves all lead to symmetric positions.
So the first 3⋅2=6 possible pairs of first moves all lead to symmetric positions.
DPatrick
2015-02-26 20:48:14
Here's a picture with the first two moves shown in blue:
Here's a picture with the first two moves shown in blue:
DPatrick
2015-02-26 20:48:19
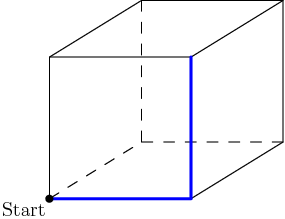

DPatrick
2015-02-26 20:48:30
We just need to count how many ways there are to finish, and multiply by 6.
We just need to count how many ways there are to finish, and multiply by 6.
Bob_Smith
2015-02-26 20:48:53
And there's only one way!
And there's only one way!
celery2
2015-02-26 20:48:53
one way to finish
one way to finish
DPatrick
2015-02-26 20:49:06
Indeed, from here, all of Erin's moved are forced! Let's see why...
Indeed, from here, all of Erin's moved are forced! Let's see why...
DPatrick
2015-02-26 20:49:17
We have to go left now: otherwise we won't reach that vertex until the end, but that's not allowed because "she is unable to return along an edge to her starting point":
We have to go left now: otherwise we won't reach that vertex until the end, but that's not allowed because "she is unable to return along an edge to her starting point":
DPatrick
2015-02-26 20:49:30
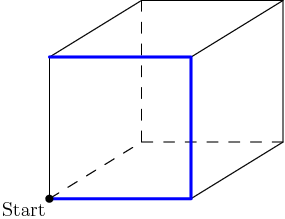

DPatrick
2015-02-26 20:49:41
And now the next move is forced:
And now the next move is forced:
DPatrick
2015-02-26 20:49:46
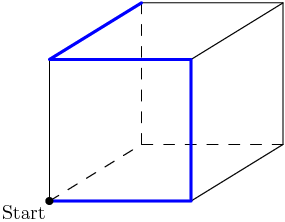

uniqueearth
2015-02-26 20:50:08
you have to go down
you have to go down
acegikmoqsuwy2000
2015-02-26 20:50:08
and we now go down
and we now go down
AMN300
2015-02-26 20:50:08
now there's only 1 good way
now there's only 1 good way
DPatrick
2015-02-26 20:50:17
And now we have to move around the back face...but we have to go counterclockwise, because if we go clockwise then we'll end at the corner adjacent to Start, which is not allowed.
And now we have to move around the back face...but we have to go counterclockwise, because if we go clockwise then we'll end at the corner adjacent to Start, which is not allowed.
DPatrick
2015-02-26 20:50:22
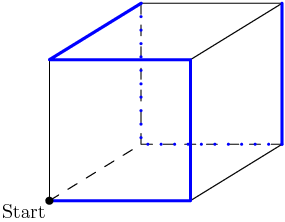

DPatrick
2015-02-26 20:50:37
So after the first two moves, all the rest of the moves are forced.
So after the first two moves, all the rest of the moves are forced.
crosby87
2015-02-26 20:50:50
answer is 6 A
answer is 6 A
SimonSun
2015-02-26 20:50:50
so A 6
so A 6
akaashp11
2015-02-26 20:50:50
A
A
celery2
2015-02-26 20:50:50
so the answer is 1x6=6 (A)
so the answer is 1x6=6 (A)
DPatrick
2015-02-26 20:50:51
So there are only 6 paths. Answer (A).
So there are only 6 paths. Answer (A).
DPatrick
2015-02-26 20:51:12
That was sort of interesting I guess.
That was sort of interesting I guess.
DPatrick
2015-02-26 20:51:36
12B #20 was not (in my opinion), but let's do it anyway...
12B #20 was not (in my opinion), but let's do it anyway...
DPatrick
2015-02-26 20:51:40
20. For every positive integer n, let mod5(n) be the remainder obtained when n is divided by 5. Define a function f:{0,1,2,3,…}×{0,1,2,3,4}→{0,1,2,3,4} recursively as follows:
f(i,j)={mod5(j+1)if i=0 and 0≤j≤4,f(i−1,1)if i≥1 and j=0, andf(i−1,f(i,j−1))if i≥1 and 1≤j≤4.
What is f(2015,2)?
12B:20
(A) 0 (B) 1 (C) 2 (D) 3 (E) 4
20. For every positive integer n, let mod5(n) be the remainder obtained when n is divided by 5. Define a function f:{0,1,2,3,…}×{0,1,2,3,4}→{0,1,2,3,4} recursively as follows:
f(i,j)={mod5(j+1)if i=0 and 0≤j≤4,f(i−1,1)if i≥1 and j=0, andf(i−1,f(i,j−1))if i≥1 and 1≤j≤4.
What is f(2015,2)?
12B:20
(A) 0 (B) 1 (C) 2 (D) 3 (E) 4
DPatrick
2015-02-26 20:51:57
Wow.
Wow.
Darn
2015-02-26 20:52:27
That looks ugly, so list out a table of values?
That looks ugly, so list out a table of values?
DrMath
2015-02-26 20:52:27
ok lets play around...
ok lets play around...
DPatrick
2015-02-26 20:52:36
Yeah, let's just try to make a little chart of this function for small values of i, and see if we notice any patterns.
Yeah, let's just try to make a little chart of this function for small values of i, and see if we notice any patterns.
DPatrick
2015-02-26 20:52:46
i=0 is pretty straightforward: we just add 1 to j and take the value mod 5.
i=0 is pretty straightforward: we just add 1 to j and take the value mod 5.
DPatrick
2015-02-26 20:52:52
ji=00112233440
ji=00112233440
DPatrick
2015-02-26 20:53:02
Let's now look at i=1. First, I'll just put in the instructions from the function:
Let's now look at i=1. First, I'll just put in the instructions from the function:
DPatrick
2015-02-26 20:53:06
ji=0i=101f(0,1)12f(0,f(1,0))23f(0,f(1,1))34f(0,f(1,2))40f(0,f(1,3))
ji=0i=101f(0,1)12f(0,f(1,0))23f(0,f(1,1))34f(0,f(1,2))40f(0,f(1,3))
DPatrick
2015-02-26 20:53:30
f(0,j) is just j+1 (mod 5), so that's write it that way:
f(0,j) is just j+1 (mod 5), so that's write it that way:
DPatrick
2015-02-26 20:53:34
ji=0i=101212f(1,0)+123f(1,1)+134f(1,2)+140f(1,3)+1
ji=0i=101212f(1,0)+123f(1,1)+134f(1,2)+140f(1,3)+1
Darn
2015-02-26 20:53:49
2,3,4,0,1
2,3,4,0,1
celery2
2015-02-26 20:53:49
2,3,4,0,1
2,3,4,0,1
Darn
2015-02-26 20:53:49
Keep adding 1
Keep adding 1
brian22
2015-02-26 20:53:49
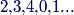
DPatrick
2015-02-26 20:53:50
Now it's clear: we just add 1 to the number above.
Now it's clear: we just add 1 to the number above.
DPatrick
2015-02-26 20:53:56
ji=0i=1012123234340401
ji=0i=1012123234340401
DPatrick
2015-02-26 20:54:10
So it looks like f(1,j)=j+2 (mod 5).
So it looks like f(1,j)=j+2 (mod 5).
DPatrick
2015-02-26 20:54:23
Hmmm...maybe we guess that f(2,j)=j+3 (mod 5).
Hmmm...maybe we guess that f(2,j)=j+3 (mod 5).
DPatrick
2015-02-26 20:54:33
Let's see...
Let's see...
DPatrick
2015-02-26 20:54:37
ji=0i=1i=20123123f(2,0)+2234f(2,1)+2340f(2,2)+2401f(2,3)+2
ji=0i=1i=20123123f(2,0)+2234f(2,1)+2340f(2,2)+2401f(2,3)+2
DPatrick
2015-02-26 20:54:52
So each number is 2 plus the number above (mod 5). That works out to:
So each number is 2 plus the number above (mod 5). That works out to:
DPatrick
2015-02-26 20:54:57
ji=0i=1i=201231230234234044011
ji=0i=1i=201231230234234044011
DPatrick
2015-02-26 20:55:14
Now the function appears to be f(2,j)=2(j−1).
Now the function appears to be f(2,j)=2(j−1).
DPatrick
2015-02-26 20:55:30
So let's move on to i=3:
So let's move on to i=3:
DPatrick
2015-02-26 20:55:35
ji=0i=1i=2i=30123012302(f(3,0)−1)23422(f(3,1)−1)34042(f(3,2)−1)40112(f(3,3)−1)
ji=0i=1i=2i=30123012302(f(3,0)−1)23422(f(3,1)−1)34042(f(3,2)−1)40112(f(3,3)−1)
DPatrick
2015-02-26 20:55:53
In other words, we subtract 1 from the number above, and then double it, then take mod 5.
In other words, we subtract 1 from the number above, and then double it, then take mod 5.
DPatrick
2015-02-26 20:56:04
This gives
This gives
DPatrick
2015-02-26 20:56:08
ji=0i=1i=2i=30123012303234243404140110
ji=0i=1i=2i=30123012303234243404140110
RJ810
2015-02-26 20:56:23
There is no 2!
There is no 2!
DPatrick
2015-02-26 20:56:30
Yes. Note that we've lost 2 as an output of the function, and that because of the recursive nature of the function, we can never get 2 as a value again. That allows us to eliminate (C).
Yes. Note that we've lost 2 as an output of the function, and that because of the recursive nature of the function, we can never get 2 as a value again. That allows us to eliminate (C).
Darn
2015-02-26 20:56:52
maybe it will continue to eliminate terms?
maybe it will continue to eliminate terms?
DPatrick
2015-02-26 20:56:58
Let's hope so, and soon!
Let's hope so, and soon!
DPatrick
2015-02-26 20:57:03
Let's continue:
Let's continue:
DPatrick
2015-02-26 20:57:06
ji=0i=1i=2i=3i=401230312303f(3,f(4,0))23424f(3,f(4,1))34041f(3,f(4,2))40110f(3,f(4,3))
ji=0i=1i=2i=3i=401230312303f(3,f(4,0))23424f(3,f(4,1))34041f(3,f(4,2))40110f(3,f(4,3))
DPatrick
2015-02-26 20:57:29
Let's just grind through them...
Let's just grind through them...
DPatrick
2015-02-26 20:57:41
f(4,0)=3, so f(4,1)=f(3,3)=1.
f(4,0)=3, so f(4,1)=f(3,3)=1.
DPatrick
2015-02-26 20:57:50
Then f(4,2)=f(3,1)=3.
Then f(4,2)=f(3,1)=3.
DPatrick
2015-02-26 20:57:56
Then f(4,3)=f(3,3)=1.
Then f(4,3)=f(3,3)=1.
DPatrick
2015-02-26 20:58:01
And finally f(4,4)=f(3,1)=3.
And finally f(4,4)=f(3,1)=3.
DPatrick
2015-02-26 20:58:09
ji=0i=1i=2i=3i=4012303123031234243340411401103
ji=0i=1i=2i=3i=4012303123031234243340411401103
acegikmoqsuwy2000
2015-02-26 20:58:15
so 4 and 0 are gone
so 4 and 0 are gone
RJ810
2015-02-26 20:58:15
There is no 4 and no 0!
There is no 4 and no 0!
abean077
2015-02-26 20:58:15
4 and 0 are gone too
4 and 0 are gone too
DPatrick
2015-02-26 20:58:20
Now the answer must be 1 or 3. 50-50 chance!
Now the answer must be 1 or 3. 50-50 chance!
DPatrick
2015-02-26 20:58:30
Maybe i=5 will finally provide some clarity:
Maybe i=5 will finally provide some clarity:
DPatrick
2015-02-26 20:58:35
ji=0i=1i=2i=3i=4i=50123031123031f(4,f(5,0))234243f(4,f(5,1))340411f(4,f(5,2))401103f(4,f(5,3))
ji=0i=1i=2i=3i=4i=50123031123031f(4,f(5,0))234243f(4,f(5,1))340411f(4,f(5,2))401103f(4,f(5,3))
DPatrick
2015-02-26 20:58:46
Again, let's just grind through them.
Again, let's just grind through them.
DPatrick
2015-02-26 20:59:01
f(5,0)=1, so f(5,1)=f(4,1)=1.
f(5,0)=1, so f(5,1)=f(4,1)=1.
abean077
2015-02-26 20:59:09
They're all 1
They're all 1
Darn
2015-02-26 20:59:09
Just 1,1,1,1,1
Just 1,1,1,1,1
DPatrick
2015-02-26 20:59:13
Aha---they're all 1! They're all f(4,the number above) and since that number above is always 1, they're all f(4,1)=1.
Aha---they're all 1! They're all f(4,the number above) and since that number above is always 1, they're all f(4,1)=1.
DPatrick
2015-02-26 20:59:25
So f(5,j)=1 for all j.
So f(5,j)=1 for all j.
trumpeter
2015-02-26 20:59:31
from i=5 and on, the output will only be 1!
from i=5 and on, the output will only be 1!
DPatrick
2015-02-26 20:59:45
Right, f(i,j) for i>5 are all 1 too! Since f(i,j)=f(i−1,something), once f(i,j)=1 at i=5, it'll be the constant function 1 for all larger i.
Right, f(i,j) for i>5 are all 1 too! Since f(i,j)=f(i−1,something), once f(i,j)=1 at i=5, it'll be the constant function 1 for all larger i.
dli00105
2015-02-26 20:59:57
answer (B)
answer (B)
acegikmoqsuwy2000
2015-02-26 20:59:57
So (B) 1
So (B) 1
sharmag
2015-02-26 20:59:57
therefore the answer is B (1)
therefore the answer is B (1)
AMN300
2015-02-26 20:59:57
so since it's recursive, the answer is 1 B
so since it's recursive, the answer is 1 B
NewbieGamer
2015-02-26 20:59:57
the answer is (B) 1
the answer is (B) 1
DPatrick
2015-02-26 21:00:00
Thus our final answer is (B) 1.
Thus our final answer is (B) 1.
DPatrick
2015-02-26 21:00:06
Wow, that problem was boring. Sorry. I don't know of a clever way.
Wow, that problem was boring. Sorry. I don't know of a clever way.
DPatrick
2015-02-26 21:00:39
Kinda sad to end on that problem, but it's 9 PM ET / 6 PM PT, so I'm afraid we're done for the evening! Thanks for coming!
Kinda sad to end on that problem, but it's 9 PM ET / 6 PM PT, so I'm afraid we're done for the evening! Thanks for coming!
DPatrick
2015-02-26 21:00:46
Please join us again on Saturday March 21 and Friday March 27 when we will be discussing the AIME I and II contests.
Please join us again on Saturday March 21 and Friday March 27 when we will be discussing the AIME I and II contests.
nosaj
2015-02-26 21:00:53
Will Richard be making videos?
Will Richard be making videos?
anandiyer12
2015-02-26 21:00:53
will videos come out?
will videos come out?
DPatrick
2015-02-26 21:01:04
I don't believe so -- he usually only makes videos for the A contests.
I don't believe so -- he usually only makes videos for the A contests.
DPatrick
2015-02-26 21:01:28
Plus we're all super-busy with last-minute details to get ready for the new AoPS website launch this weekend!
Plus we're all super-busy with last-minute details to get ready for the new AoPS website launch this weekend!
DrMath
2015-02-26 21:01:48
what about the guy in the black hoodie that looks suspiciously like him?
what about the guy in the black hoodie that looks suspiciously like him?
DPatrick
2015-02-26 21:01:58
Maybe he has some free time, but he never responds to my friend requests.
Maybe he has some free time, but he never responds to my friend requests.
awesomenesspanda
2015-02-26 21:02:12
So approximately when will the answer key come out?
So approximately when will the answer key come out?
DPatrick
2015-02-26 21:02:25
I would guess that the AMC will put up an answer key very soon. But I have no idea for sure.
I would guess that the AMC will put up an answer key very soon. But I have no idea for sure.
rockyisi
2015-02-26 21:02:36
when will all the solutions come out?
when will all the solutions come out?
DPatrick
2015-02-26 21:02:56
A copy of the solutions was sent to every school. The AMC never posts full solutions.
A copy of the solutions was sent to every school. The AMC never posts full solutions.
thequantumguy
2015-02-26 21:03:21
when will the cut off be posted
when will the cut off be posted
DPatrick
2015-02-26 21:03:23
I have no idea.
I have no idea.
nosaj
2015-02-26 21:03:36
Thanks for putting in a lot of work on the new site!
Thanks for putting in a lot of work on the new site!
hnkevin42
2015-02-26 21:03:36
Excited for the new website for AoPS!
Excited for the new website for AoPS!
DPatrick
2015-02-26 21:03:39
Thanks -- we are too!
Thanks -- we are too!
DPatrick
2015-02-26 21:04:17
OK, I need to kick you all out of the classroom so that I can generate and post the transcript of the session. Have a good night!
OK, I need to kick you all out of the classroom so that I can generate and post the transcript of the session. Have a good night!
AkhilY
2015-02-26 21:04:49
where can we find the transcript
where can we find the transcript
DPatrick
2015-02-26 21:05:18
School -> MathJams, then the Transcripts link.
School -> MathJams, then the Transcripts link.
DPatrick
2015-02-26 21:05:28
(Not for another 5-10 minutes though. I'll also post the link on the Forum.)
(Not for another 5-10 minutes though. I'll also post the link on the Forum.)
RevL8ion
2015-02-26 21:06:51
Thanks again for the Math Jam!
Thanks again for the Math Jam!
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.









