A system with a combination.

by individ, Jun 29, 2025, 5:24 PM

[url]https://math.stackexchange.com/questions/5079425/find-all-a-b-c-in-bbb-n-a-b-c-gt-1-such-that-abc-1-bac-1-an [/url]

It is better to solve the problem in a general way.

$\left\{\!\begin{aligned} & ab+T=cq \\ & ac+T=bt \\ & bc+T=af \end{aligned}\right.$
We factor out the number $T$ as follows.

$T=Ap((B-A)t-p(A+1)^2)$
Then the solutions can be written as follows.

$\left\{\!\begin{aligned} & a=(A+1)p \\ & b=A(B+1)p \\ & c=A(A+1)p+At \\ & q=(B-A)p \\ & t=t \\ & f=A(AB-1)p+ABt \end{aligned}\right.$

number theory

Diophantine equation

system of equations

How to describe all integer solutions to?

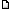by individ, Jun 26, 2025, 1:27 PM

[url]https://mathoverflow.net/questions/415173/how-to-describe-all-integer-solutions-to-x2y2-z31/496760#496760 [/url]

It is quite difficult to obtain parametrization of all solutions of the equation.

$X^2+Y^2=Z^3+1$
Therefore, I think it's worth making several attempts at a solution, it's quite possible that which one will give the result.

If we use solutions of the Pell equation. $P^2-2S^2=1$

$\left[\!\begin{aligned} & P=pp_0+2ss_0 \\ & S=sp_0+ps_0 \end{aligned}\right.$
Let's introduce the coefficients.

$\left[\!\begin{aligned} & a=2s(s\pm{p})L\pm{p^2}+2ps\pm{2s^2} \\ & b=p(p\pm{2s})L\pm{p^2}+2ps\pm{2s^2} \\ & k=(p^2\pm2ps+2s^2)L\pm{p^2}+4ps\pm{2s^2} \end{aligned}\right.$
$\left[\!\begin{aligned} & X=bk^2+ak-b \\ & Y=ak^2-bk-a \\ & Z=k^2 \end{aligned}\right.$
For solutions of the Pell equations of the form.

$P^2-(3k^2+2t^2)S^2=1$
$\left[\!\begin{aligned} & a=p^2-2tps+(2t^2+6kt-3k^2)s^2 \\ & b=2p^2-2(3k+t)ps+(6k^2+6kt-2t^2)s^2 \\ & k=p^2-2(2k+t)ps+k(3k+2t)s^2 \end{aligned}\right.$
$\left[\!\begin{aligned} & a=p^2-2tps+(2t^2+6kt-3k^2)s^2 \\ & b=p^2+2tps+(3k^2+6kt-4t^2)s^2 \\ & k=2(k+t)ps+2t(k-t)s^2 \end{aligned}\right.$
$\left[\!\begin{aligned} & X=3bk^2+3ak-b \\ & Y=3ak^2-3bk-a \\ & Z=3k^2+1 \end{aligned}\right.$

number theory

Diophantine equation

Integer solutions of....

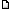by individ, Jun 25, 2025, 2:21 PM

https://mathoverflow.net/questions/203435/integer-solutions-of-x2-48y213z2/496717#496717

Let's look at the general case.

$aX^2+bY^2=cZ^2+N$
When the coefficients of this equation are not represented in the form of squares. Then a funny pattern emerges.
If we know some solution to the equation and we know any solution to the Pell equation. Then we can always construct the following solution to this equation.

$\left\{\!\begin{aligned} & ax^2+bY^2=cz^2+N \\ & cp^2-as^2=1 \end{aligned}\right.$
Formally, the relationship between the solvability of the Lagrange equation in general and the solvability of the equivalent Pell equation is obtained.

Numbers can have any signs.

$f=\sqrt{ac(sz+px)^2+by^2-N}$
$\left\{\!\begin{aligned} & X=cxp^2+fs+czps \\ & Z=axps+pf+azs^2 \end{aligned}\right.$
$\left\{\!\begin{aligned} & X=cxp^2-2czps+axs^2 \\ & Z=czp^2-2axps+azs^2 \end{aligned}\right.$
Solutions to the general equation.

$cp^2-as^2=1$
They are found using solutions.

$\left\{\!\begin{aligned} & q^2-can^2=1 \\ & ck^2-at^2=1 \end{aligned}\right.$
$\left\{\!\begin{aligned} & p=qk+atn \\ & s=qt+cnk \end{aligned}\right.$
Consider the example mentioned in the question.

$8X^2+13Y^2=Z^2-4$
$X=1 ; Y=1 ; Z=5$

$a=8 ; b=13 ; c=1$

Solutions to the Pell equation $p^2-8s^2=1$

$(p ; s) - (3 ; 1)$

$\left\{\!\begin{aligned} & P=3p+8s \\ & S=3s+p \end{aligned}\right.$
We substitute it and get it. The first gives $(x;Y;z) - (1597;1;4517)$ , the second $(x;Y;z)-(443;1;1253)$

For any value of $(X,Y)$ , an infinite number of solutions are obtained.

number theory

Diophantine equation

A variant of the solution of the general quadratic equation.

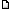by individ, Jun 25, 2025, 10:22 AM

https://math.stackexchange.com/questions/4624896/all-natural-number-solutions-for-the-equation-a2b2-2c2
Let's look at the general case.

$aX^2+bY^2=cZ^2$
When the coefficients of this equation are not represented in the form of squares. Then a funny pattern emerges.

If we know some solution to the equation and we know any solution to the Pell equation. Then we can always construct the following solution to this equation.

$\left\{\!\begin{aligned} & ax^2+by^2=cz^2 \\ & cp^2-as^2=1 \end{aligned}\right.$
$f=\sqrt{ac(sz+px)^2+by^2}$
$\left\{\!\begin{aligned} & X=cxp^2+fs+czps \\ & Z=axps+pf+azs^2 \end{aligned}\right.$
Formally, the relationship between the solvability of the Lagrange equation in general and the solvability of the equivalent Pell equation is obtained. Numbers can have any signs.

This post has been edited 1 time. Last edited by individ, Jun 25, 2025, 1:14 PM

number theory

Diophantine equation

Polynomial parametrization for solutions of quadratic Diophantine equations

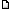by individ, Jun 19, 2025, 9:16 AM

https://mathoverflow.net/questions/425040/polynomial-parametrization-for-solutions-of-quadratic-diophantine-equations

On the solvability of the equation.

$xy-zt=N$
Any parameterization , if we want it to be complete. It must describe all the numbers, solutions for example for $y$ . It must describe all the numbers from $1, 2, 3, ... \infty$

At the same time, $z$ and $t$ must be independent of each other. And the only parameter that depends on the rest is $x$ .

Factorize the number. $N=ab$

$x=ap+k(py-b)$ $y=y$ $z=ky+a$ $t=py-b$

number theory

Diophantine equation

The Markov equation in general form

by individ, Jun 18, 2025, 4:49 PM

https://mathoverflow.net/questions/392993/on-markoff-type-diophantine-equation

It is worth mentioning the method of finding solutions to a general equation.

$aX^2+bY^2+cZ^2=dXYZ+e$
Since this is the general Pell equation. Then all solutions can be found by knowing the solutions of the following equations.

$ax^2+by^2+cz^2=dxyz+e$
$ap^2-dzps+bs^2=1$
The solutions can be written in this form.

$X=(dzy-ax)p^2-2byps+bxs^2$
$Y=ayp^2-2axps+(dzx-by)s^2$
To build solutions, you need to know the solutions.
$aP^2-dzPS+bS^2=1$

Knowing any two solutions.

$ak^2-dzkt+bt^2=1$

$ap^2-dzps+bs^2=1$

The rest of the solutions can be obtained.
$P=(dzt-ka)p^2-2tbps+bks^2$ $S=atp^2-2akps+(dzt-kb)s^2$

This post has been edited 2 times. Last edited by individ, Jun 18, 2025, 4:53 PM

number theory

Diophantine equation

Congruent numbers

by individ, Jun 17, 2025, 5:32 AM

https://math.stackexchange.com/questions/1576861/on-p2-nq2-z2-p2-nq2-t2-and-the-congruent-number-problem

If we know of any solution to the system.
$\left\{\begin{aligned}&a^2+pb^2=k^2\\&a^2+qb^2=t^2\end{aligned}\right.$

Then for the system

$\left\{\begin{aligned}&x^2+py^2=z^2\\&x^2+qy^2=v^2\end{aligned}\right.$
You can write a solution

$x=a^2k^2-pb^2t^2=a^2t^2-qb^2k^2$ $y=2akbt$ $z=a^2k^2+pb^2t^2$ $v=a^2t^2+qb^2k^2$

number theory

Diophantine equation

system of equations

Erdős-Straus conjecture

by individ, Jun 15, 2025, 9:36 AM

[url]https://math.stackexchange.com/questions/450280/erdős-straus-conjecture/5075634#5075634[/url]

Still, it's worth considering the general case.
$\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{q}{t}$
I gave a lot of formulas, but all of them somehow boiled down to the need to factor $t=ab$ . And the solution somehow boils down to this form.

$\frac{1}{kps}+\frac{1}{ap}+\frac{1}{bs}=\frac{q}{t}$
The task actually boils down to finding a single number.

$p=\frac{kbs+t}{k(qs-a)}$
And getting solutions is going through all the possible options. Going through all the options does not require a lot of calculations. I'll show you an example of the question I was asked.

The meaning of the search is in another record. Separate the whole part and consider the case when the remainder is whole.

$p=\frac{kbs+t}{k(qs-a)}=C+\frac{k(b-Cq)s+t+kaC}{k(qs-a)}$
I'll give you an example. $\frac{q}{t}=\frac{4}{73}$

Let. $a=1$ $;$ $b=73$

$p=\frac{73sk+73}{k(4s-1)}$
Let. $k=73$

$p=\frac{73s+1}{4s-1}=18+\frac{s+19}{4s-1}$
In this case, it is enough to check the numbers. $s=1,2,3,4,5,6,7$

There is no point in checking further. Because the remainder becomes less than 1, and we only need integers.

And the solution will be numbers.

$s=2 ; p=21$ $...$ $x=73*2*21 ; y=21 ; z=73*2$

$s=3 ; p=20$ $...$ $x=73*20*3 ; y=20 ; z=73*3$

number theory

Diophantine equation

The sum of any two elements is a square

by individ, Jun 12, 2025, 5:09 PM

https://math.stackexchange.com/questions/952801/biggest-set-such-that-sum-of-any-pair-is-perfect-square/952806#952806

After the publication of the solution in this form, there were many questions about the too cumbersome formula. It turns out that many people may not like the formula.

Therefore, I made an attempt to find a much easier parameterization of the solutions of this system.

$\left. \begin{aligned} b+a=x^2\\ a+c=e^2\\ b+c=y^2\\ a+f=j^2\\ b+f=z^2\\ c+f=p^2 \end{aligned} \right\}$
The numbers can be found using the formulas

$b=\frac{x^2+y^2-e^2}{2}$ $a=\frac{e^2+x^2-y^2}{2}$ $c=\frac{e^2+y^2-x^2}{2}$ $f=\frac{2z^2+e^2-x^2-y^2}{2}$
The parameterization of the solution can be written as.

$z=50t^2-60ts+50s^2+2z^2-10(t+s)z$ $e=25t^2-30ts+25s^2-z^2$ $y=-25t^2-50st+55s^2-z^2+4z(5t-3s)$ $j=50t^2-100st+10s^2-2z^2+16sz$ $x=10t^2-100st+50s^2-2z^2+16tz$ $p=55t^2-50st-25s^2-z^2+4z(5s-3t)$
$P.S. ---$

I understand that there are two questions. This is the desire of some to use a computer to sort through all the solutions and present the solutions in a different form. Therefore, it is worth adding a few words.
Expressing numbers in terms of squares, we formulate the problem in a different way. We are looking for the number $N$ , which can be represented as the sum of squares in 3 different ways.

$N=z^2+e^2=y^2+j^2=x^2+p^2$
The formula is known and the solution can be written down.

https://artofproblemsolving.com/community/c3046h1359115_representation_of_a_number_the_squares_in_different_ways_2

$z=t(n^2+k^2)(s^2+k^2)$ $e=g(n^2+k^2)(s^2+k^2)$ $y=((n^2-k^2)t-2nkg)(s^2+k^2)$ $j=((n^2-k^2)g+2nkt)(s^2+k^2)$ $x=((s^2-k^2)t-2skg)(n^2+k^2)$ $p=((s^2-k^2)g+2skt)(n^2+k^2)$

This post has been edited 2 times. Last edited by individ, Jun 16, 2025, 4:11 PM

number theory

Diophantine equation

system of equations

A system of similar nonlinear equations

by individ, Dec 29, 2022, 12:45 PM

There is a whole group of such systems of equations.

$\left\{\!\begin{aligned} & A^2+AB+B^2=C^2 \\ & F^2+FZ+Z^2=C^2 \end{aligned}\right.$
Such a system is solved as standard. First, we write down the parametrization of one equation.

$A=p^2-s^2$
$B=s(s+2p)$
$C=p^2+ps+s^2=x^2+xy+y^2$
$F=x^2-y^2$
$Z=y(y+2x)$
And then we find the parameterization for the necessary parameters.

$p=2q^2+2qt-t^2-3qk+k^2$
$s=-q^2+2qt+2t^2-3tk+k^2$
$y=q^2+qt+t^2-k^2$
$x=q^2+qt+t^2-3(q+t)k+2k^2$

Diophantine equation

system of equations

number theory

Submit

How did you discover these parametric solutions to diophantine equations?
by fanzhuyifan, Dec 31, 2016, 9:25 AM
Russian? are you sure it ain't greek?
by Mathisfun04, Dec 27, 2016, 4:03 PM
yep i agree
by Eugenis, Oct 31, 2015, 2:40 AM
Best blog ever
by FlakeLCR, Oct 13, 2015, 8:07 PM
too much russian.
by rileywkong, Aug 21, 2015, 6:10 PM
Decided the equation.
by individ, Aug 20, 2015, 5:05 AM
Some insight into how you figured it out?
by Not_a_Username, Aug 19, 2015, 3:52 PM
I figured it out. Decided equation.
by individ, Aug 19, 2015, 5:01 AM
Yes, how do you come up with the formula?
by Not_a_Username, Aug 18, 2015, 10:29 PM
I don't understand. There are the equation and there is a formula to it solutions. What is the problem?
by individ, Aug 13, 2015, 4:22 PM
What? Lol you are substituting solutions with literally no motivation
by Not_a_Username, Aug 13, 2015, 12:59 PM
What replacement? Where?
by individ, Aug 8, 2015, 5:37 AM
Darn, what are the motivation for these substitutions???
by Not_a_Username, Aug 5, 2015, 10:44 AM
Are you greek?
by beanielove2, Dec 24, 2014, 6:31 PM
So, a purely mathematical blog?
by Lionfish, Dec 2, 2014, 1:20 PM
To prove that it is necessary to show the method of calculation. I do not want to do yet.
by individ, Mar 28, 2014, 6:14 AM
I can't understand these posts....What language are they written in? I don't recognize it.

I like your avatar!
by 15cjames, Mar 11, 2014, 1:57 PM

17 shouts

individ's blog

by individ, Jun 29, 2025, 5:24 PM

by individ, Jun 26, 2025, 1:27 PM

by individ, Jun 25, 2025, 2:21 PM

by individ, Jun 25, 2025, 10:22 AM

by individ, Jun 19, 2025, 9:16 AM

by individ, Jun 18, 2025, 4:49 PM

by individ, Jun 17, 2025, 5:32 AM

by individ, Jun 15, 2025, 9:36 AM

by individ, Jun 12, 2025, 5:09 PM

by individ, Dec 29, 2022, 12:45 PM