Два квадрата и куб.

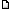by individ, Mar 24, 2014, 6:41 AM

the equation:

$X^2+Y^2=Z^3$

Has the solutions:

$X=2k^6+8tk^5+2(7t^2+8qt-9q^2)k^4+16(t^3+2qt^2-tq^2-2q^3)k^3+$

$+2(7t^4+12qt^3+6q^2t^2-28tq^3-9q^4)k^2+8(t^5+2qt^4-2q^3t^2-5tq^4)k+$

$+2(q^6-4tq^5-5q^4t^2-5q^2t^4+4qt^5+t^6)$

.................................................................................................................................................

$Y=2k^6+4(3q+t)k^5+2(9q^2+16qt+t^2)k^4+32qt(2q+t)k^3+$

$+2(-9q^4+20tq^3+30q^2t^2+12qt^3-t^4)k^2+$

$+4(-3q^5-tq^4+10q^3t^2+6q^2t^3+5qt^4-t^5)k-$

$-2(q^6+4tq^5-5q^4t^2-5q^2t^4-4qt^5+t^6)$

.................................................................................................................................................

$Z=2k^4+4(q+t)k^3+4(q+t)^2k^2+4(q^3+tq^2+qt^2+t^3)k+2(q^2+t^2)^2$

$q,t,k$ - What are some integers any sign. After substituting the numbers and get a result it will be necessary to divide by the greatest common divisor. This is to obtain the primitive solutions.
number theory
Diophantine equation

Comment

1 Comment

The post below has been deleted. Click to close.
This post has been deleted. Click here to see post.
Hi, how you got this solution? This is wonderful!

by ersh, Jan 1, 2019, 9:05 PM

Archives
- December 2022
A system of similar nonlinear equations
The problem of 4 cubes
The problem of 4 cubes
Sequences of cubes
Sequences of cubes
Sequences of cubes
The problem of 4 cubes
The problem of 4 cubes
+ October 2022
Prove that a+b+c+d is a composite number
The Pell equation
+ January 2022
Find all positive integers s.t.
+ February 2021
A Class of Diophantine Equations in Three Variables
+ December 2019
Finding positive integer number solution of system of Diophantine equation
+ September 2019
Combination of three...
+ July 2019
Five dice.
The Diophantine equation always has infinitely many solutions.
+ June 2019
All the integer solutions of a certain semi-algebraic system
+ May 2019
Representation of a square of a certain shape.
+ July 2018
Amount and combination.
Nontrivial integer solutions.
+ June 2018
System of diophantine equalions.
+ May 2018
Infinite positive integer solutions of the equation.
+ January 2018
Symmetric system of several Diophantine equations.
+ December 2017
Three square sums solution structures
+ November 2017
Parameterization of ......
+ October 2017
System from the forum.
+ September 2017
Erdős-Straus conjecture
Characterising all integer solutions.
Question about parametric divisibility relations
+ August 2017
Sum of two consecutive squares equals difference of two cons
How prove infinitely many postive integers triples
A system without solutions.
+ July 2017
The sum of the fractions.
System in the form of progression.
+ May 2017
View the sum of cubes.
Factorization.
+ April 2017
The decomposition of unity!
Factorization.
The sum of squares.
+ March 2017
Nearly symmetrical equation.
The numbers are the sum of the squares of h 2.
+ February 2017
Number representation using polynomials.
System with factorization.
For the system of equations. One suggestion.
+ January 2017
Linear system.
a combination system of equations. 2.
A variation on the curves of triangular numbers.
+ December 2016
a combination system of equations.
Some Pythagorean triplets.
Representation of a number the squares in different ways. 2
Representation of a number the squares in different ways.
System of Diophantine equations in the form of combinations.
The System Of Diophantus.
+ November 2016
Cubes with squares.
+ October 2016
The system with rational solutions.
4 squares with 3 squares.
+ September 2016
The case with rational coefficient.
+ July 2016
System with a Pythagorean triple.
+ June 2016
System with a finite number of solutions.
Reduction to the Pell equation.
+ May 2016
One symmetric equation.
One binary form.
+ April 2016
To prove that there is always a solution.
+ March 2016
The cube view.
+ January 2016
One simple formula.
The system is an arithmetic progression.
System with permutations.
Factorization. 3.
+ December 2015
Cube with 6 cubes.
A special quadratic form.
A cubic equation. With the Troika.
Combinations of numbers in squares.
+ November 2015
Quadratic equations.
Representation of a number in a square shape.
The sum of squares.
Almost binary equation.
The squares with the 4th degree.
+ October 2015
Overall look for long equations.
system of equations.
+ September 2015
System of Diophantine equations. 4,1.
2 books of Diophantus task 34 , 35.
System 2, 20A.
One factorization.
+ August 2015
Pentagonal Numbers
The system of book 2: objectives 24, 25.
The factorization.
For the system of book 2 task 30.
Nonlinear system Diophantus. book 2 tasks 22 , 23 .
Almost Pythagoras.
+ July 2015
System with 3 and 5.
Almost Pythagorean system.
+ June 2015
The system in itself.
Pythagorean triples.
A variation of the same identity.
+ May 2015
The General Pell equation.
+ April 2015
The equation of the forum.
+ March 2015
One factorization.
+ February 2015
One system of Diophantine equations.
Another solution.
Pythagorean triples.
The system of Diophantine equations. 3.
An old equation. 2
An old equation.
Almost Pythagorean triple.
Diophantine equation with cubes.
The system is almost linear Diophantine equations.
Diophantine equation with parameter.
Parametrization of solutions of diophantine equation. 4 variable
+ January 2015
The solution of a system of Diophantine equations.
Consecutive triangular numbers in a square.
Triangular numbers square.
Diophantine equation 3-rd degree.
The variation of the Pythagorean triples.
One binary form.
The system of equations 16.
Diophantine Equation With Varying Exponents
Diophantine equation $l^2+m^2+n^2=p^3+q^3$
General Pell equation.
Almost cubic Diophantine equation.
Pythagorean type diophantine equation. 2
Pythagorean type diophantine equation.
+ December 2014
The decomposition of the square.
Solve the Diophantine equation with Pell.
Factorization.
Almost Pell.
The system of Diophantine equations. 2
Quadratic Diophantine equation.
A very simple equation.
Streamlined decision of the previous equation.
One simple Diophantine equation.
Amount.
+ November 2014
The system of equations: 15
The cubes. a.
The system of Diophantine equations. Ti.
The difference.
the system of Diophantine equations a
For the system of equations:
Triangular numbers for Pythagorean triples. 2
Triangular numbers for Pythagorean triples.
The system of equations. a.
Equation with coefficients.
The squares with cube 2.
The squares of the cube.
The attitude.
Sum of squares.
This system of equations 3c.
The squares. 2
+ October 2014
The system of equations: 1.
The system of equations. 2b
The system of equations. 2a.
The upgraded formula of Legendre.
The squares. 2
The squares.
Cubes with squares.
Task quadrangle. 2
Task quadrangle.
The system of equations "b".
The system of equations "a".
Factorization. 2
Solving homogeneous quaternary quadratic Diophantine equation
Special square.
Another solution almost Pythagoras. 3
+ September 2014
Another solution almost Pythagoras.
One particular solution.
The Heron's Triangle.
One simple task.
Almost linear equation.
The use of the Pell equation for solving the Pell equation.
Almost Pythagoras.
Symmetric Diophantine equation. 2.
Almost Pythagoras.
Beautiful number.
Diophantine equation from the Greek.
+ August 2014
Easy.
Steptoe.
A simple Binary equation.
Almost Pythagoras.
The system of Diophantine equations.
Factorization.
The system of Diophantine equations:
Simple binary form.
Binary form.
Symmetric Diophantine equation.
Binary quadratic form.
Continuation .
The equation for the equation Farm.
+ July 2014
Pythagorean triple.
Almost Pythagorean triples.
Very simple Diophantine equation.
Комбинация 3.
Простое соотношение.
Разница кубов.
Более общий вариант. 2
Найти нечётные решения.
Почти комбинация.
Система 12.
Уравнение Маркова. 1
Система 11.
Полином.
Сумма кубов и сумма их комбинаций. 2
Сумма кубов и сумма их комбинаций.
+ June 2014
Куб с квадратом.
Не сложное уравнение.
Простое уравнение. 5
Одна гипотеза. 3
Одна гипотеза. 2
Одна гипотеза.
Бинарная форма. 4
Комбинация. 2
Почти Пифагор 4.
+ May 2014
Система 10.
Пифагоровы тройки. 2
Решение для кубиков.
Существование решения.
Бинарная форма. 3
Тройки. 2
Кривые треугольные числа.
Почти квадрат
Разница. 1
Почти Пифагор 3
Уравнение Эйлера.
Ещё тройки.
Задача Герона 2.
Задача Герона
Почти Пифагор. 2
+ April 2014
Квадрат с кубиком.
Простое.
Куб с квадратом 2.
Простое.
Пятёрка
Разница.
Треугольные 5
Треугольные 4.
Треугольные 3.
Сумма с квадратом.
Три с три.
Диофантово уравнение с 6 переменными.
Бинарная форма. 2
Бинарная форма.
Комбинация с комбинацией.
Пятиугольные числа.
Простое.
Тройки.
Diophantine equation Madame Zarangesh
+ March 2014
Простое уравнение. 4
Простое уравнение. 3
Простое уравнение. 2
Система 10.
Само с собой. 4 -3.
Само с собой. 5
Само с собой.
Треугольные.
Четвёрки с четвёркой.
Пифагоровы тройки.
Два квадрата и куб.
Почти Пифагор.
Уравнение с форума.
Степень 5.
Уравнение:
Комбинация.
Вторая с пятой!
Треугольное число.
Не симметричные Пифагоровы тройки. 2
Не симметричные Пифагоровы тройки.
Кубики
Почти Пифагор.
Простое.
Система 9
Комбинация числа.
Простое уравнение.
Система 9
Система 8
Ещё 1 решение.
Плохое решение.
Пифагоровы четвёрки с -1.
Система 7
+ February 2014
Система 6
Система 5
Решение для кого то. 1
Кубики с кубиками.
Более общий вариант.
Ещё решение.
Ещё одно решение.
Дробное уравнение
Уравнение Маркова.
Кубик
Куб с квадратом
Система 4
Каша
Четвёрки
Проект Эйлера
Одно уравнение 2
Одно уравнение
Самое капризное уравнение и
Самое капризное уравнение 3
Самое капризное уравнение 2
Самое капризное уравнение
5 степень.
Уравнение мадам Зарангеш.
Два на два
Уравнение Лежандра
Пифагоровы тройки и решения Пелля. 2
Система 3
Четвёрка треугольных
Треугольные
Кубики 2
3
Четвёрки с коэффициентами 2
Четвёрки с коэффициентами
Четвёрки с Эйлером.
Кубики
Пифагоровы четвёрки
Кубы 2.
Из книжки.
Бинарная квадратичная форма.
Кубы
Треугольные числа.
Уравнение Эйлера
Система2
Система.1
Пифагоровы тройки и решения Пелля.
Уравнение Лежандра.
формулы решения диофантовых уравнений
Shouts
Submit

  • How did you discover these parametric solutions to diophantine equations?

    by fanzhuyifan, Dec 31, 2016, 9:25 AM

  • Russian? are you sure it ain't greek?

    by Mathisfun04, Dec 27, 2016, 4:03 PM

  • yep i agree

    by Eugenis, Oct 31, 2015, 2:40 AM

  • Best blog ever

    by FlakeLCR, Oct 13, 2015, 8:07 PM

  • too much russian.

    by rileywkong, Aug 21, 2015, 6:10 PM

  • Decided the equation.

    by individ, Aug 20, 2015, 5:05 AM

  • Some insight into how you figured it out?

    by Not_a_Username, Aug 19, 2015, 3:52 PM

  • I figured it out. Decided equation.

    by individ, Aug 19, 2015, 5:01 AM

  • Yes, how do you come up with the formula? :P

    by Not_a_Username, Aug 18, 2015, 10:29 PM

  • I don't understand. There are the equation and there is a formula to it solutions. What is the problem?

    by individ, Aug 13, 2015, 4:22 PM

  • What? Lol you are substituting solutions with literally no motivation

    by Not_a_Username, Aug 13, 2015, 12:59 PM

  • What replacement? Where?

    by individ, Aug 8, 2015, 5:37 AM

  • Darn, what are the motivation for these substitutions???

    by Not_a_Username, Aug 5, 2015, 10:44 AM

  • Are you greek?

    by beanielove2, Dec 24, 2014, 6:31 PM

  • So, a purely mathematical blog?

    by Lionfish, Dec 2, 2014, 1:20 PM

  • To prove that it is necessary to show the method of calculation. I do not want to do yet.

    by individ, Mar 28, 2014, 6:14 AM

  • I can't understand these posts....What language are they written in? I don't recognize it.

    I like your avatar! :P

    by 15cjames, Mar 11, 2014, 1:57 PM

17 shouts
Tags
Diophantine equation
number theory
system of equations
About Owner
  • Posts: 494
  • Joined: Feb 12, 2014
Blog Stats
  • Blog created: Feb 13, 2014
  • Total entries: 323
  • Total visits: 98039
  • Total comments: 24
Search Blog